التحقق الرسمي المتقدم من أدلة المعرفة الصفرية: كيفية إثبات ذاكرة المعرفة الصفرية

في سلسلة مدوناتنا حول التحقق الرسمي المتقدم من أدلة المعرفة الصفرية لقد ناقشنا كيفية التحقق من تعليمات ZK و الغوص العميق في اثنين من نقاط الضعف في ZK من خلال التحقق رسميًا من كل تعليمات zkWasm، وجدنا كل ثغرة أمنية واحدة وقمنا بإصلاحها، مما يسمح لنا بالتحقق الكامل من السلامة الفنية وصحة دائرة zkWasm بأكملها، كما هو موضح في تقرير عام و مستودع الكود .

على الرغم من أننا أظهرنا عملية التحقق من تعليمات zkWasm وقدمنا المفاهيم الأولية للمشروع، فقد يكون القراء المألوفون بالتحقق الرسمي مهتمين بفهم تفرد zkVM مقارنة بأنظمة ZK الأصغر الأخرى أو الأنواع الأخرى من آلات البايت كود الافتراضية في التحقق. في هذه المقالة، سنناقش بالتفصيل بعض النقاط الفنية التي واجهتها عند التحقق من نظام ذاكرة zkWasm. الذاكرة هي الجزء الأكثر تفردًا في zkVM، والتعامل معها بشكل جيد أمر بالغ الأهمية للتحقق من جميع آلات zkVM الأخرى.

التحقق الرسمي: الآلة الافتراضية (VM) مقابل الآلة الافتراضية ZK (zkVM)

هدفنا النهائي هو التحقق من صحة zkWasm على غرار نظريات صحة مفسّر البايت كود العادي (VM، مثل مفسّر EVM الذي تستخدمه عقد Ethereum). أي أن كل خطوة تنفيذ للمفسّر تتوافق مع خطوة قانونية بناءً على الدلالات التشغيلية للغة. كما هو موضح في الشكل أدناه، إذا كانت الحالة الحالية لبنية بيانات مفسّر البايت كود هي SL، وتم وضع علامة على هذه الحالة على أنها حالة SH في المواصفات عالية المستوى لجهاز Wasm، فعندما يخطو المفسّر إلى حالة SL، يجب أن تكون هناك حالة SH قانونية عالية المستوى مقابلة، وتنص مواصفات Wasm على أن SH يجب أن يخطو إلى SH.

وبالمثل، فإن zkVM لديه نظرية صحة مماثلة: كل صف جديد في جدول تنفيذ zkWasm يتوافق مع خطوة قانونية بناءً على الدلالات التشغيلية للغة. كما هو موضح في الشكل أدناه، إذا كانت الحالة الحالية لصف من بنية بيانات جدول التنفيذ هي SR، وتم تمثيل هذه الحالة كحالة SH في المواصفات عالية المستوى لجهاز Wasm، فيجب أن يتوافق الصف التالي من حالة جدول التنفيذ SR مع حالة SH عالية المستوى، وتنص مواصفات Wasm على أن SH يجب أن تنتقل إلى SH.

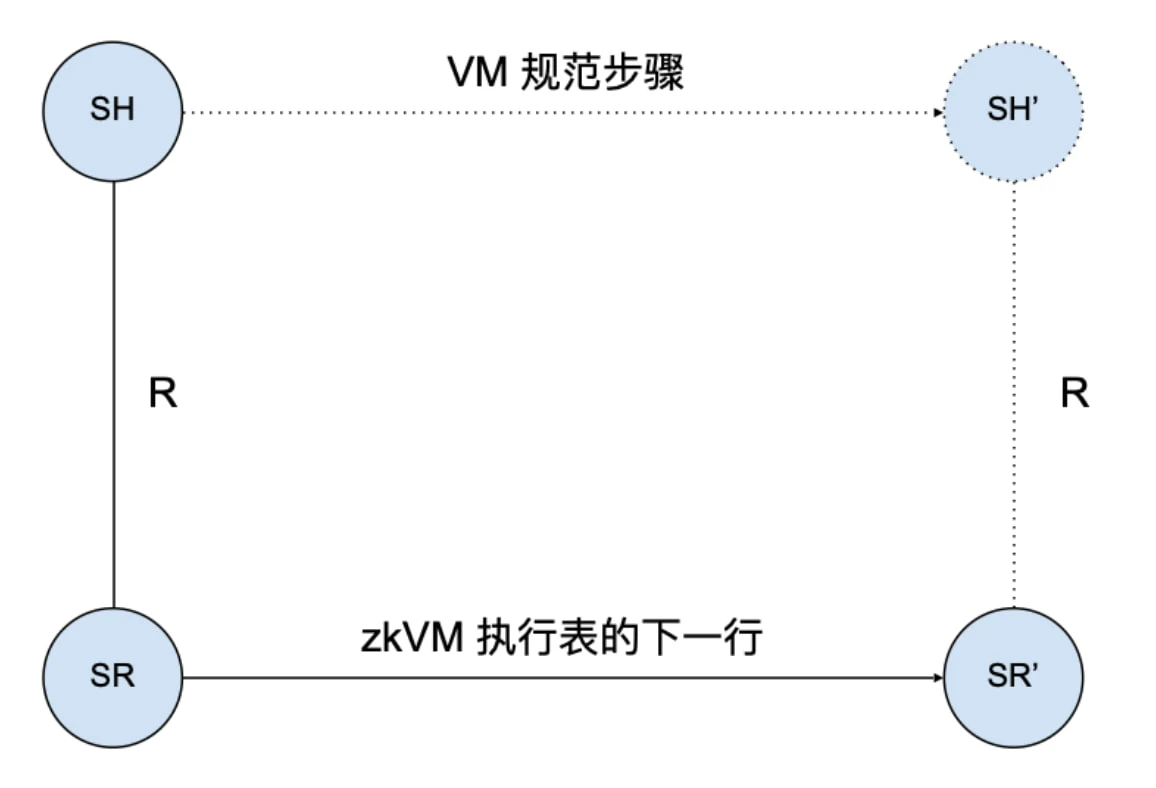يمكن ملاحظة أن مواصفات الحالة عالية المستوى وخطوات Wasm متسقة في كل من VM وzkVM، لذا يمكن استخدام خبرة التحقق السابقة لمفسري أو مترجمي لغة البرمجة كمرجع. تكمن الميزة الخاصة للتحقق من zkVM في نوع بنية البيانات التي تشكل الحالة منخفضة المستوى للنظام.

أولاً، كما وصفنا في تدوينة سابقة إن أدوات إثبات zk هي في الأساس عمليات حسابية صحيحة مع تعديل الأعداد الأولية الكبيرة، وتتعامل مواصفات Wasm والمترجمون العاديون مع الأعداد الصحيحة ذات 32 بت أو 64 بت. ويتعامل جزء كبير من تنفيذ zkVM مع هذا، لذا فإن التحقق يحتاج إلى التعامل مع هذا أيضًا. ومع ذلك، فهذه مشكلة محلية: يصبح كل سطر من التعليمات البرمجية أكثر تعقيدًا لأنه يحتاج إلى التعامل مع العمليات الحسابية، ولكن الهيكل العام للتعليمات البرمجية والإثبات لا يتغير.

هناك فرق كبير آخر وهو كيفية التعامل مع هياكل البيانات ذات الحجم الديناميكي. في مفسّر البايت كود العادي، يتم تنفيذ الذاكرة ومكدس البيانات ومكدس النداء كهياكل بيانات قابلة للتغيير. وعلى نحو مماثل، تمثل مواصفات Wasm الذاكرة كنوع بيانات باستخدام طرق get/set. على سبيل المثال، يحتوي مفسّر Geths EVM على نوع بيانات `Memory` يتم تنفيذه كصفيف بايت يمثل الذاكرة الفعلية ويتم كتابته وقراءته من خلال طرق `Set 32` و`GetPtr`. لتنفيذ تعليمات تخزين الذاكرة يقوم Geth باستدعاء `Set 32` لتعديل الذاكرة المادية.

دالة opMstore(pc *uint 64، المترجم *EVMInterpreter، النطاق *ScopeContext) ([] بايت، خطأ) {

//قيمة البوب للمكدس

mStart، القيمة := نطاق.Stack.pop()، نطاق.Stack.pop()

النطاق.الذاكرة.المجموعة 32(mStart.Uint 64()، القيمة)

العودة صفر، صفر

}

في إثبات صحة المترجم أعلاه، من السهل نسبيًا إثبات أن الحالة عالية المستوى تطابق الحالة منخفضة المستوى بعد تعيين القيم للذاكرة الملموسة في المترجم والذاكرة المجردة في المواصفات.

ومع ذلك، مع zkVM، تصبح الأمور أكثر تعقيدًا.

جدول ذاكرة zkWasms وطبقة تجريد الذاكرة

في zkVM، يحتوي جدول التنفيذ على أعمدة للبيانات ذات الحجم الثابت (على غرار السجلات في وحدة المعالجة المركزية)، لكنه لا يستطيع التعامل مع هياكل البيانات ذات الحجم الديناميكي، والتي يمكن الوصول إليها من خلال الجداول المساعدة. يحتوي جدول تنفيذ zkWasm على عمود EID بقيم 1 و2 و3 وما إلى ذلك، وجدولين مساعدين، جدول الذاكرة وجدول الانتقال، لتمثيل بيانات الذاكرة ومكدس النداء على التوالي.

فيما يلي مثال لتنفيذ برنامج الانسحاب:

الرصيد الدولي، المبلغ؛

الفراغ الرئيسي () {

الرصيد = 100؛

المبلغ = 10؛

الرصيد -= المبلغ; // سحب

}

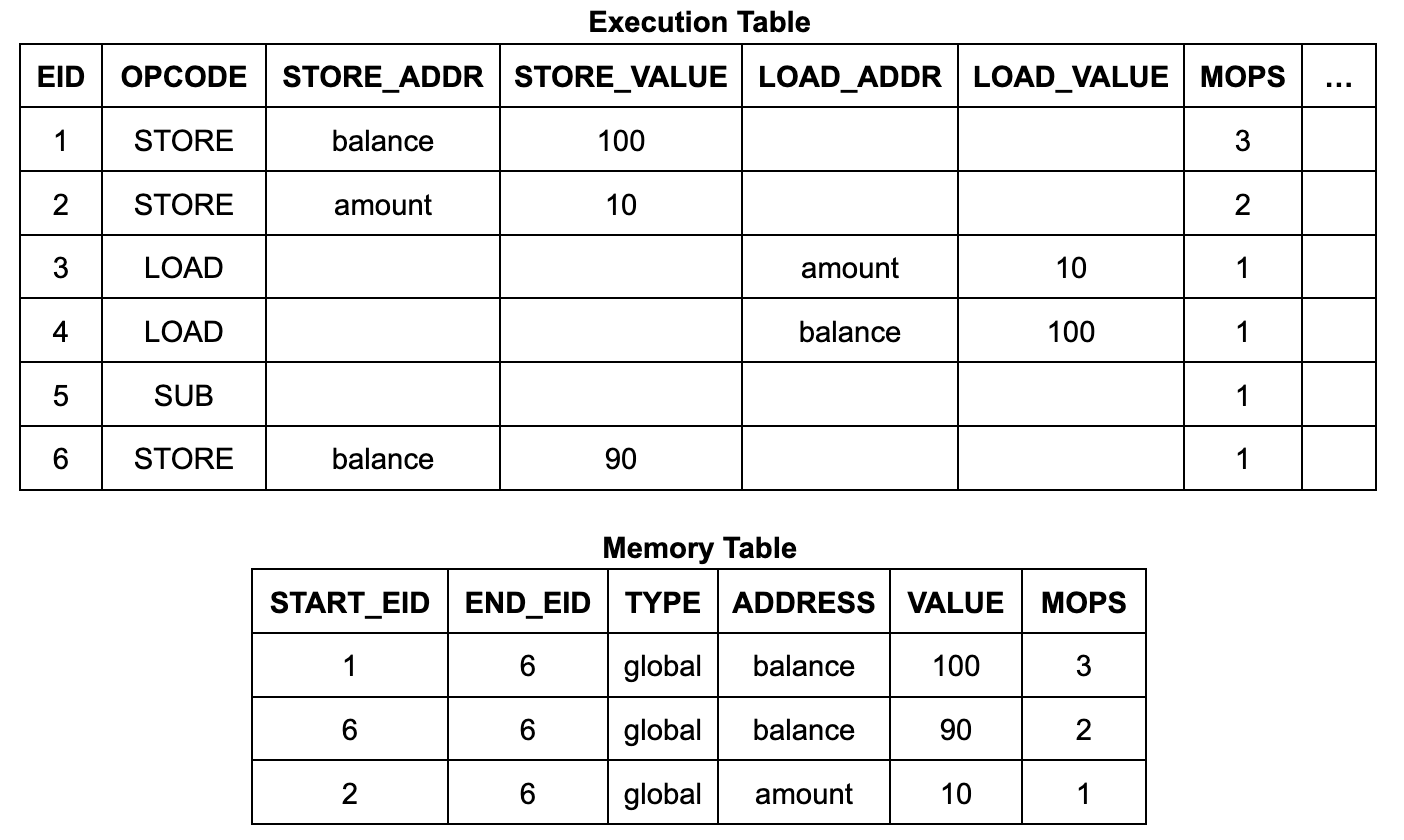
محتويات وبنية جدول التنفيذ بسيطة إلى حد ما. فهو يحتوي على 6 خطوات تنفيذ (EIDs من 1 إلى 6)، وكل منها تحتوي على صف يسرد رمز العملية (opcode)، وإذا كانت التعليمات عبارة عن قراءة أو كتابة في الذاكرة، فيتم إدراج عنوانها وبياناتها:

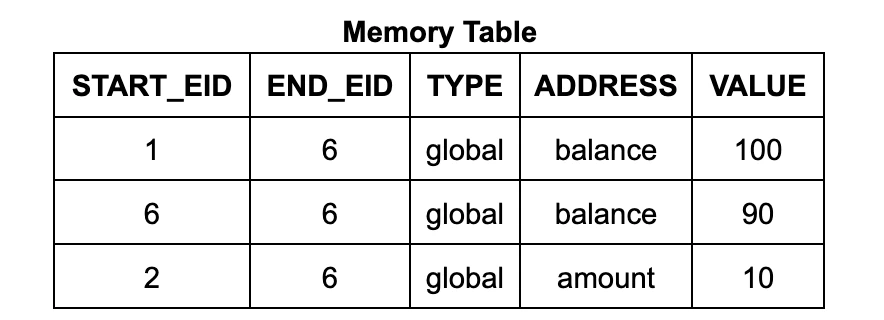
يحتوي كل صف في جدول الذاكرة على عنوان وبيانات ومعرف بداية ومعرف نهاية. معرف البداية هو معرف خطوة التنفيذ التي كتبت البيانات إلى هذا العنوان، ومعرف النهاية هو معرف خطوة التنفيذ التالية التي ستكتب إلى هذا العنوان. (كما يحتوي على عدد، والذي سنناقشه بالتفصيل لاحقًا.) بالنسبة لدائرة تعليمات القراءة في ذاكرة Wasm، فهي تستخدم قيد بحث للتأكد من وجود إدخال جدول مناسب في الجدول بحيث يكون معرف تعليمات القراءة في النطاق من البداية إلى النهاية. (وبالمثل، يتوافق كل صف في جدول القفز مع إطار من مكدس النداء، ويتم تسمية كل صف بمعرف خطوة تعليمات الاستدعاء التي أنشأته.)

يختلف نظام الذاكرة هذا بشكل كبير عن مفسّر الآلة الافتراضية العادي: فجدول الذاكرة ليس ذاكرة قابلة للتغيير يتم تحديثها تدريجيًا، ولكنه يحتوي على تاريخ جميع عمليات الوصول إلى الذاكرة في مسار التنفيذ بالكامل. ومن أجل تبسيط عمل المبرمجين، يوفر zkWasm طبقة تجريد يتم تنفيذها من خلال دالتين إدخال ملائمتين. وهما:

تخصيص_ذاكرة_الجدول_البحث_عن_كتابة_الخلية

و

تخصيص_ذاكرة_الجدول_البحث_عن_قراءة_الخلية

معامالاتها هي كما يلي:

على سبيل المثال، يحتوي الكود الذي ينفذ تعليمات تخزين الذاكرة في zkWasm على استدعاء لوظيفة تخصيص الكتابة:

دع memory_table_lookup_heap_write1 = المخصص

.alloc_memory_table_lookup_write_cell_with_value(

تخزين كتابة الدقة 1،

مُنشئ القيود،

عيد,

نقل |____| ثابت_من!(LocationType::Heap as u 64)،

نقل |meta| load_block_index.expr(meta)، // العنوان

نقل |____| ثابت_من!(0)، // هو 32 بت

نقل |____| ثابت_من!( 1)، // (دائمًا) ممكّن

);

دع store_value_in_heap1 = memory_table_lookup_heap_write1.value_cell؛

وظيفة `alloc` مسؤولة عن التعامل مع قيود البحث بين الجداول والقيود الحسابية التي تربط `eid` الحالي بإدخال جدول الذاكرة. وبالتالي، يمكن للمبرمج التعامل مع هذه الجداول كذاكرة عادية، وبعد تنفيذ الكود، يتم تعيين قيمة `store_value_in_heap1` إلى عنوان `load_block_index`.

على نحو مماثل، يتم تنفيذ تعليمات قراءة الذاكرة باستخدام الدالة `read_alloc`. في تسلسل التنفيذ المثال أعلاه، تحتوي كل تعليمة تحميل على قيد قراءة وتحتوي كل تعليمة تخزين على قيد كتابة، ويتم تلبية كل قيد من خلال إدخال في جدول الذاكرة.

mtable_lookup_write(الصف 1.eid، الصف 1.عنوان_المتجر، الصف 1.قيمة_المتجر)

⇐ (الصف 1.eid= 1 ∧ الصف 1.store_addr=الرصيد ∧ الصف 1.store_value= 100 ∧ …)

mtable_lookup_write(الصف 2.eid، الصف 2.عنوان_المتجر، الصف 2.قيمة_المتجر)

⇐ (الصف 2.eid= 2 ∧ الصف 2.store_addr=amount ∧ الصف 2.store_value= 10 ∧ …)

mtable_lookup_read(الصف 3.eid، الصف 3.load_addr، الصف 3.load_value)

⇐ ( 2

mtable_lookup_read(الصف 4.eid، الصف 4.load_addr، الصف 4.load_value)

⇐ ( 1

mtable_lookup_write(الصف 6.eid، الصف 6.عنوان_المتجر، الصف 6.قيمة_المتجر)

⇐ (الصف 6.eid= 6 ∧ الصف 6.store_addr=الرصيد ∧ الصف 6.store_value= 90 ∧ …)

يجب أن يتوافق هيكل التحقق الرسمي مع التجريدات المستخدمة في البرنامج الذي يتم التحقق منه، بحيث يمكن للإثبات أن يتبع نفس منطق الكود. بالنسبة لـ zkWasm، يعني هذا أننا بحاجة إلى التحقق من دائرة جدول الذاكرة ووظيفة خلية القراءة/الكتابة المخصصة كوحدة نمطية، مع واجهة مثل الذاكرة القابلة للتغيير. في ظل وجود مثل هذه الواجهة، يمكن إجراء التحقق من كل دائرة تعليمات بطريقة مماثلة للمترجم العادي، مع تعقيد ZK الإضافي المغلف في وحدة نظام فرعي للذاكرة.

في عملية التحقق، قمنا بتنفيذ فكرة مفادها أن جدول الذاكرة يمكن اعتباره في الواقع بنية بيانات قابلة للتغيير. أي أننا كتبنا دالة `memory_at type`، والتي تقوم بمسح جدول الذاكرة بالكامل وبناء تعيين بيانات العنوان المقابل. (هنا، نطاق قيمة المتغير `type` هو ثلاثة أنواع مختلفة من بيانات ذاكرة Wasm: الكومة، ومكدس البيانات، والمتغيرات العالمية.) ثم أثبتنا أن قيود الذاكرة التي تولدها دالة التخصيص تعادل تغييرات البيانات التي تم إجراؤها على تعيين بيانات العنوان المقابل باستخدام دالتي set وget. يمكننا إثبات أن:

• بالنسبة لكل عيد، إذا كانت القيود التالية صحيحة

قيمة إزاحة نوع eid لـ memory_table_lookup_read_cell

لكن

الحصول على (نوع الذاكرة في eid) الإزاحة = بعض القيمة

• وإذا كانت القيود التالية صحيحة

memory_table_lookup_write_cell قيمة إزاحة النوع eid

لكن

memory_at (eid+ 1) type = set (memory_at eid type) offset value

بعد ذلك، يمكن التحقق من كل تعليمة بناءً على عمليات الحصول والتعيين على تعيين عنوان البيانات، على غرار مفسر البايت كود غير ZK.

آلية حساب الكتابة في الذاكرة zkWasms

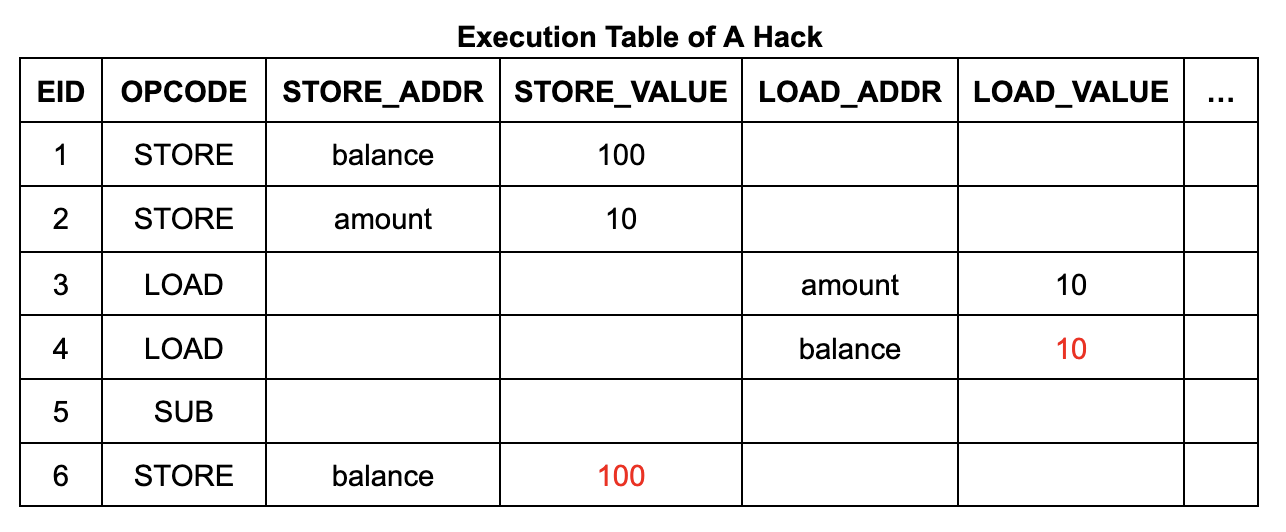
ومع ذلك، لا يكشف الوصف المبسّط أعلاه عن المحتويات الكاملة لجدول الذاكرة وجدول الانتقال. في إطار عمل zkVM، يمكن للمهاجم التلاعب بهذه الجداول، حيث يمكنه بسهولة التلاعب بتعليمات تحميل الذاكرة لإرجاع قيمة عشوائية عن طريق إدخال صف من البيانات.

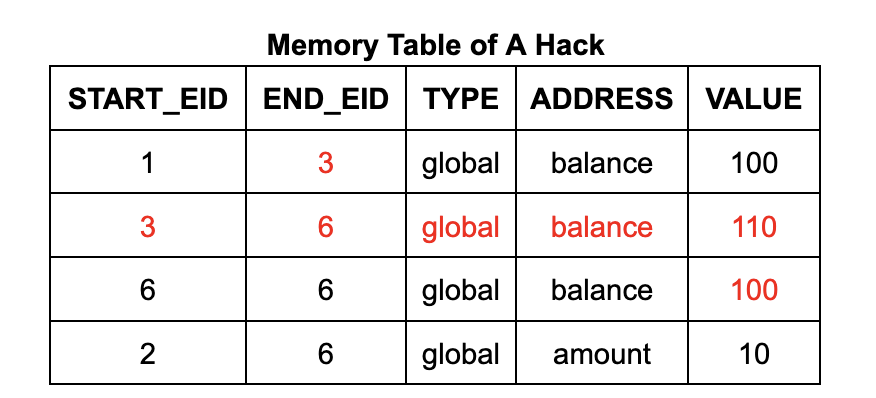
إذا أخذنا برنامج السحب كمثال، فإن المهاجم لديه الفرصة لحقن بيانات زائفة في رصيد الحساب من خلال تزوير عملية كتابة الذاكرة $110 قبل عملية السحب. ويمكن تحقيق هذه العملية من خلال إضافة صف من البيانات إلى جدول الذاكرة وتعديل قيم الخلايا الموجودة في جدول الذاكرة وجدول التنفيذ. سيؤدي هذا إلى عملية سحب مجانية، لأن رصيد الحساب سيظل عند $100 بعد العملية.

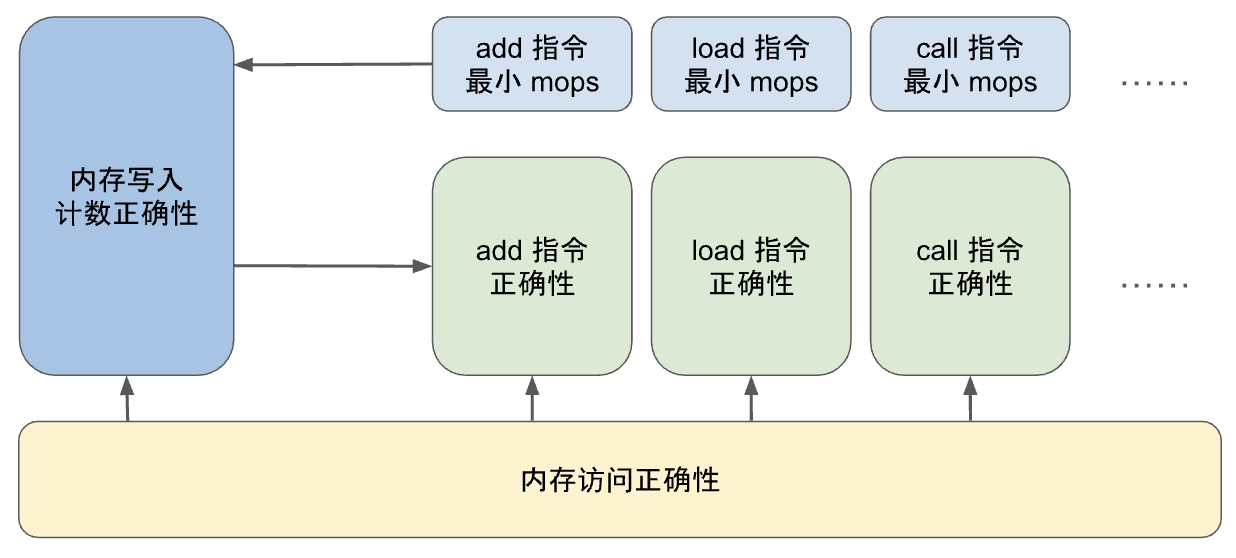
للتأكد من أن جدول الذاكرة (وجدول القفز) يحتوي فقط على إدخالات صالحة تم إنشاؤها بواسطة عمليات الكتابة في الذاكرة (والمكالمات والإرجاعات) التي يتم تنفيذها بالفعل، يستخدم zkWasm آلية عد خاصة لمراقبة عدد الإدخالات. على وجه التحديد، يحتوي جدول الذاكرة على عمود مخصص يتتبع العدد الإجمالي لإدخالات الكتابة في الذاكرة. في نفس الوقت، يحتوي جدول التنفيذ أيضًا على عداد يحسب عدد عمليات الكتابة في الذاكرة المتوقعة لكل تعليمة. يتم تعيين قيد المساواة لضمان اتساق العدين. منطق هذا النهج بديهي للغاية: في كل مرة يتم فيها تنفيذ عملية كتابة في الذاكرة، يتم عدها مرة واحدة، ويجب أن يكون هناك سجل مقابل في جدول الذاكرة. لذلك، لا يمكن للمهاجم إدراج أي إدخالات إضافية في جدول الذاكرة.

العبارة المنطقية أعلاه غامضة بعض الشيء، وفي عملية الإثبات الميكانيكي، نحتاج إلى جعلها أكثر دقة. أولاً، نحتاج إلى تصحيح عبارة مبرهنة الكتابة في الذاكرة المذكورة أعلاه. نقوم بتعريف دالة `mops_at eid type` التي تحسب عدد إدخالات جدول الذاكرة باستخدام `eid` و`type` معينين (ستنشئ معظم التعليمات 0 أو 1 إدخالاً عند eid). تحتوي العبارة الكاملة للنظرية على شرط مسبق إضافي ينص على عدم وجود إدخالات زائفة في جدول الذاكرة:

إذا كانت القيود التالية صحيحة

(قيمة إزاحة نوع eid لـ memory_table_lookup_write_cell)

وتظل القيود الجديدة التالية سارية

(mops_at eid type) = 1

لكن

(memory_at(eid+ 1) type) = تعيين قيمة الإزاحة (memory_at eid type)

يتطلب هذا أن يكون التحقق لدينا أكثر دقة من الحالة السابقة. لا يكفي أن نستنتج ببساطة من قيد المساواة أن العدد الإجمالي لإدخالات جدول الذاكرة يساوي العدد الإجمالي للكتابات في الذاكرة أثناء التنفيذ. من أجل إثبات صحة التعليمات، نحتاج إلى معرفة أن كل تعليمة تتوافق مع العدد الصحيح لإدخالات جدول الذاكرة. على سبيل المثال، نحتاج إلى استبعاد إمكانية أن يحذف المهاجم إدخال جدول الذاكرة لتعليمة في تسلسل التنفيذ وينشئ إدخالًا جديدًا ضارًا في جدول الذاكرة لتعليمة أخرى غير ذات صلة.

ولإثبات ذلك، نتبع نهجًا من أعلى إلى أسفل لتقييد عدد إدخالات جدول الذاكرة لتعليمة معينة، والذي يتكون من ثلاث خطوات. أولاً، نقوم بتقدير عدد الإدخالات التي يجب إنشاؤها للتعليمات في تسلسل التنفيذ، بناءً على نوع التعليمات. نطلق على العدد المتوقع للكتابات من الخطوة رقم i إلى نهاية التنفيذ `instructions_mops i`، والعدد المقابل لإدخالات جدول الذاكرة من التعليمات رقم i إلى نهاية التنفيذ `cum_mops (eid i)`. من خلال تحليل قيود البحث لكل تعليمة، يمكننا إثبات أنها لا تنشئ إدخالات أقل من المتوقع، وبالتالي فإن كل جزء [i… numRows] يتم تعقبه لا ينشئ إدخالات أقل من المتوقع:

Lemma cum_mops_bound: لجميع ni،

0 ≤ ي ->

i + Z.of_nat n = etable_numRow ->

MTable.cum_mops (etable_values eid_cell i) (max_eid+ 1) ≥ instructions_mops i n.

ثانياً، إذا كان بوسعنا أن نظهر أن الجدول لا يحتوي على عدد من الإدخالات أكثر من المتوقع، فهذا يعني أنه يحتوي على العدد الصحيح من الإدخالات، وهذا أمر واضح.

Lemma cum_mops_equal : لجميع ni،

0 ≤ ي ->

i + Z.of_nat n = etable_numRow ->

MTable.cum_mops (etable_values eid_cell i) (max_eid+ 1) ≤ instructions_mops في ->

MTable.cum_mops (etable_values eid_cell i) (max_eid+ 1) = instructions_mops i n.

الآن نأتي للخطوة 3. تنص نظرية الصحة لدينا على أنه بالنسبة لأي n، فإن cum_mops و instruction_mops تتفقان دائمًا في جزء الجدول من الصف n إلى النهاية:

Lemma cum_mops_equal : لجميع n،

0

MTable.cum_mops (etable_values eid_cell (Z.of_nat n)) (max_eid+ 1) = instructions_mops (Z.of_nat n)

يتم التحقق عن طريق الاستقراء على n. الصف الأول في الجدول هو قيد المساواة لـ zkWasm، والذي ينص على أن العدد الإجمالي للإدخالات في جدول الذاكرة صحيح، أي cum_mops 0 = instructions_mops 0. بالنسبة للصفوف التالية، تخبرنا فرضية الاستقراء بما يلي:

cum_mops n = تعليمات_mops n

ونأمل أن نثبت

cum_mops (n+ 1) = instructions_mops (n+ 1)

ملحوظة هنا

cum_mops n = mop_at n + cum_mops (n+ 1)

و

تعليمات_ممسحات n = تعليمات_ممسحات n + تعليمات_ممسحات (n+ 1)

لذلك، يمكننا الحصول على

mops_at n + cum_mops (n+ 1) = instruction_mops n + instruction_mops (n+ 1)

لقد أظهرنا سابقًا أن كل تعليمة ستنشئ عددًا لا يقل عن العدد المتوقع من الإدخالات، على سبيل المثال

mops_at n ≥ instruction_mops n.

لذلك يمكن الاستنتاج

cum_mops (n+ 1) ≤ instructions_mops (n+ 1)

وهنا نحتاج إلى تطبيق المبدأ الثاني المذكور أعلاه.

(يمكن تطبيق فرضية مماثلة على جداول القفز لإثبات أن كل تعليمة استدعاء تولد إدخالًا واحدًا فقط في جدول القفز، مما يجعل أسلوب الإثبات قابلاً للتطبيق بشكل عام. ومع ذلك، هناك حاجة إلى مزيد من العمل لإثبات صحة تعليمات الإرجاع. يختلف معرف الإرجاع عن معرف تعليمات الاستدعاء التي أنشأت إطار الاستدعاء، لذلك نحتاج إلى ثابت إضافي (وهو ما ينص على أن قيمة eid تتزايد بشكل أحادي الاتجاه في تسلسل التنفيذ.)

إن هذا الوصف التفصيلي للإثبات هو أمر طبيعي في التحقق الرسمي وهو السبب وراء أن التحقق من جزء معين من الكود يستغرق وقتًا أطول من كتابته. ولكن هل يستحق الأمر ذلك؟ في هذه الحالة، يستحق ذلك، لأنه أثناء الإثبات اكتشفنا خطأً خطيرًا في آلية عد جدول القفز. وقد تم وصف هذا الخطأ بالتفصيل في المنشور السابق – باختصار، كانت النسخة القديمة من الكود تحسب كلًا من تعليمات الاستدعاء والإرجاع، وكان بإمكان المهاجم أن يفسح المجال لإدخال جدول قفزة مزيف عن طريق إضافة تعليمة إرجاع إضافية إلى تسلسل التنفيذ. ورغم أن آلية العد غير الصحيحة تلبي حدس حساب كل تعليمات الاستدعاء والإرجاع، فإن المشاكل تصبح واضحة عندما نحاول تحسين هذا الحدس إلى بيان نظري أكثر دقة.

تقسيم عملية الإثبات إلى وحدات

من المناقشة أعلاه، يمكننا أن نرى أن هناك تبعية دائرية بين الإثبات حول كل دائرة تعليمات والإثبات حول عمود العد في جدول التنفيذ. لإثبات صحة دائرة التعليمات، نحتاج إلى التفكير في عمليات الكتابة في الذاكرة فيها؛ أي أننا نحتاج إلى معرفة عدد إدخالات جدول الذاكرة عند EID معين، ونحتاج إلى إثبات أن عدد عمليات الكتابة في الذاكرة في جدول التنفيذ صحيح؛ وهو ما يتطلب بدوره إثبات أن كل تعليمة تؤدي على الأقل الحد الأدنى لعدد عمليات الكتابة في الذاكرة.

بالإضافة إلى ذلك، هناك عامل آخر يجب مراعاته. مشروع zkWasm كبير جدًا، لذا يجب تقسيم عمل التحقق إلى وحدات بحيث يمكن لمهندسي التحقق المتعددين تقسيم العمل. لذلك، عند تفكيك إثبات آلية العد، يجب إيلاء اهتمام خاص لتعقيدها. على سبيل المثال، بالنسبة لتعليمة LocalGet، هناك نظريتان على النحو التالي:

نظرية opcode_mops_correct_local_get : لكل i،

0

القيم القابلة للجدولة eid_cell i > 0 ->

opcode_mops_correct LocalGet i.

نظرية LocalGetOp_correct : لجميع i st y xs،

0

القيم القابلة للتنفيذ الخلية الممكنة i = 1 ->

الممسحات_في_التصحيح i ->

etable_values (ops_cell LocalGet) i = 1 ->

حالة_الارتباط في st ->

wasm_stack st = xs ->

(etable_values offset_cell i) > 1 ->

nth_error xs (Z.to_nat (etable_values offset_cell i – 1)) = Some y ->

state_rel (i+ 1) (update_stack (incr_iid st) (y::xs)).

أول بيان للنظرية

opcode_mops_correct LocalGet i

بعد توسيع التعريف، فهذا يعني أن التعليمات تنشئ إدخالًا واحدًا على الأقل في جدول الذاكرة في السطر i (يتم تحديد الرقم 1 في مواصفات التعليمات البرمجية الخاصة بـ LocalGet الخاصة بـ zkWasm).

النظرية الثانية هي نظرية الصحة الكاملة لهذه التعليمات، والتي تستشهد بـ

الممسحات_في_التصحيح

كفرضية، هذا يعني أن التعليمات تنشئ إدخالًا واحدًا فقط في جدول الذاكرة.

يمكن لمهندسي التحقق إثبات هاتين النظريتين بشكل مستقل ثم دمجهما مع الإثبات المتعلق بجدول التنفيذ لإثبات صحة النظام بأكمله. ومن الجدير بالذكر أنه يمكن إجراء جميع الإثباتات الخاصة بالتعليمات الفردية على مستوى قيود القراءة/الكتابة دون معرفة التنفيذ المحدد لجدول الذاكرة. لذلك، ينقسم المشروع إلى ثلاثة أجزاء يمكن معالجتها بشكل مستقل.

لخص

إن التحقق من صحة دوائر zkVM سطرًا بسطر لا يختلف اختلافًا جوهريًا عن التحقق من صحة تطبيقات ZK الأخرى، حيث تتطلب جميعها تفكيرًا مشابهًا فيما يتعلق بالقيود الحسابية. وعلى مستوى عالٍ، يتطلب التحقق من صحة zkVM العديد من نفس التقنيات المستخدمة في التحقق الرسمي من مفسري ومترجمي لغات البرمجة. والفرق الرئيسي هنا هو حالة الآلة الافتراضية ذات الحجم الديناميكي. ومع ذلك، يمكن تقليل تأثير هذه الاختلافات من خلال بناء بنية التحقق بعناية لتتناسب مع مستوى التجريد المستخدم في التنفيذ، بحيث يمكن التحقق من صحة كل تعليمة بشكل مستقل على أساس واجهة get-set، تمامًا كما هو الحال بالنسبة للمترجم العادي.

تم الحصول على هذه المقالة من الإنترنت: التحقق الرسمي المتقدم من أدلة المعرفة الصفرية: كيفية إثبات ذاكرة المعرفة الصفرية