Vitalik：Binius，二元域的有效证明

原文作者：Vitalik Buterin

原文翻译：Kate，MarsBit

这篇文章主要针对那些对 2019 年密码学，尤其是 SNARK 和 STARK 熟悉的读者。如果你不熟悉，我建议你先阅读这些内容。特别感谢 Justin Drake、Jim Posen、Benjamin Diamond 和 Radi Cojbasic 的反馈和评论。

在过去的两年中，STARK 已成为一种关键且不可替代的技术，可用于高效地对非常复杂的语句（例如，证明以太坊区块有效）进行易于验证的加密证明。其中一个关键原因是字段大小较小：基于椭圆曲线的 SNARK 需要您处理 256 位整数才能足够安全，而 STARK 允许您使用更小的字段大小并获得更高的效率：首先是 Goldilocks 字段（64 位整数），然后是 Mersenne 31 和 BabyBear（均为 31 位）。由于这些效率的提高，使用 Goldilocks 的 Plonky 2 在证明多种计算时比其前辈快数百倍。

一个自然而然的问题是：我们能否将这一趋势推向逻辑结论，并通过直接对零和一进行操作来构建运行速度更快的证明系统？这正是 Binius 试图做的事情，它使用了许多数学技巧，使其与三年前的 SNARK 和 STARK 截然不同。这篇文章描述了为什么小字段可以使证明生成更有效率，为什么二进制字段具有独特的强大功能，以及 Binius 用来使二进制字段上的证明如此高效的技巧。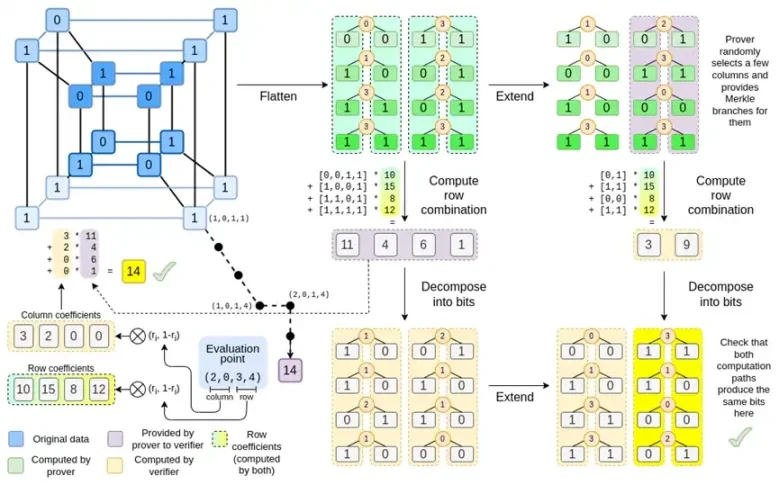

Binius，读完这篇文章后，你应该能够理解该图表的每个部分。

回顾：有限域

密码证明系统的关键任务之一是在保持数字较小的情况下对大量数据进行操作。如果你能将有关大型程序的陈述压缩为包含少量数字的数学方程，但这些数字与原始程序一样大，那么你什么也没得到。

为了在保持数字较小的情况下进行复杂的算术运算，密码学家经常使用模数算术。我们选择素数模数 p。% 运算符表示取余数：15% 7 = 1，53% 10 = 3，依此类推。（请注意，答案始终为非负数，例如 -1% 10 = 9）

您可能已经在加减时间的上下文中见过模数运算（例如，9 点 4 点是几点？）。但在这里，我们不仅仅对数字进行加减模数运算；我们还可以进行乘法、除法和取指数运算。

我们重新定义：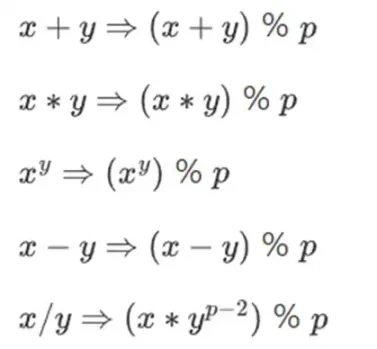

上述规则都是自洽的。例如，如果 p = 7，则：

5 + 3 = 1（因为 8% 7 = 1）

1-3 = 5（因为 -2% 7 = 5）

2* 5 = 3

3/5 = 2

这种结构的一个更通用的术语是有限域。有限域是一种遵循通常算术定律的数学结构，但其中可能值的数量是有限的，因此每个值都可以用固定的大小来表示。

模数运算（或素数域）是最常见的有限域类型，但还有另一种类型：扩展域。您可能已经见过一种扩展域：复数。我们想象一个新元素并将其标记为 i，然后对其进行数学运算：(3i+2)*(2i+4)=6i*i+12i+4i+8=16i+2。我们可以对素数域的扩展做同样的事情。当我们开始处理较小的域时，素数域的扩展对于安全性变得越来越重要，而二进制域（Binius 使用）完全依赖扩展来实现实用性。

回顾：算术化

SNARK 和 STARK 证明计算机程序的方式是通过算术：你对想要证明的程序提出一个陈述，然后将其转化为涉及多项式的数学方程。方程的有效解对应于程序的有效执行。

举一个简单的例子，假设我计算了第 100 个斐波那契数，我想向你证明它是什么。我创建一个多项式 F，对斐波那契数列进行编码：因此 F(0)=F(1)=1、F(2)=2、F(3)=3、F(4)=5，以此类推，共 100 步。我需要证明的条件是 F(x+2)=F(x)+F(x+1) 在整个范围 x={0, 1…98} 上。我可以通过给出商来说服你：

其中 Z(x) = (x-0) * (x-1) * …(x-98)。如果我能保证 F 和 H 满足这个等式，那么 F 就必须在范围内满足 F(x+ 2)-F(x+ 1)-F(x)。如果我另外验证 F 的 F(0)=F(1)=1，那么 F(100) 实际上一定是第 100 个斐波那契数。

如果你想证明更复杂的东西，那么你可以用一个更复杂的方程来代替简单的关系 F(x+2) = F(x) + F(x+1)，这个方程基本上说 F(x+1) 是用状态 F(x) 初始化虚拟机的输出，然后运行一个计算步骤。你也可以用更大的数字（例如 100000000）代替数字 100，以适应更多步骤。

所有 SNARK 和 STARK 都基于使用多项式（有时是向量和矩阵）上的简单方程来表示单个值之间的大量关系的理念。并非所有算法都会像上面那样检查相邻计算步骤之间的等价性：例如，PLONK 不会，R1CS 也不会。但许多最有效的检查都会这样做，因为通过多次执行相同的检查（或相同的几个检查），可以更轻松地最大限度地减少开销。

Plonky 2：从 256 位 SNARK 和 STARK 到 64 位……只有 STARK

五年前，对不同类型的零知识证明的合理总结如下。有两种类型的证明：（基于椭圆曲线的）SNARK 和（基于哈希的）STARK。从技术上讲，STARK 是一种 SNARK，但在实践中，通常使用“SNARK”来指代基于椭圆曲线的变体，使用“STARK”来指代基于哈希的构造。SNARK 很小，因此您可以非常快速地验证它们并轻松将它们安装在链上。STARK 很大，但它们不需要可信设置，并且具有抗量子性。

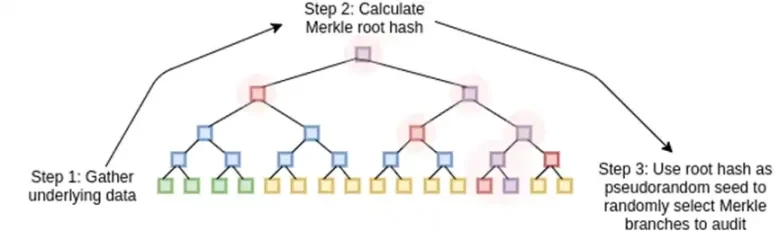
STARK 的工作原理是将数据视为多项式，计算该多项式的计算，并使用扩展数据的 Merkle 根作为“多项式承诺”。

这里的一个关键历史是，基于椭圆曲线的 SNARK 首先被广泛使用：由于 FRI，STARK 直到 2018 年左右才变得足够高效，而那时 Zcash 已经运行了一年多。基于椭圆曲线的 SNARK 有一个关键限制：如果你想使用基于椭圆曲线的 SNARK，那么这些方程中的算术必须以椭圆曲线上的点数为模来完成。这是一个很大的数字，通常接近 2 的 256 次方：例如，对于 bn128 曲线，它是 21888242871839275222246405745257275088548364400416034343698204186575808495617。但真正的计算使用较小的数字：如果你考虑用你最喜欢的语言编写的真实程序，它使用的大部分东西是计数器、for 循环中的索引、程序中的位置、表示 True 或 False 的单个位，以及几乎总是只有几位数字的其他东西。

即使原始数据由小数字组成，证明过程也需要计算商、扩展、随机线性组合和其他数据转换，这些转换将产生相等或更多数量的对象，这些对象的平均大小与字段的整个大小一样大。这造成了一个关键的低效率：要证明对 n 个小值的计算，您必须对 n 个大得多的值进行更多计算。最初，STARK 继承了使用 256 位字段的 SNARK 习惯，因此遭受了同样的低效率。

某些多项式求值的 Reed-Solomon 展开。尽管原始值很小，但附加值会扩展为字段的整个大小（在本例中为 2^31 – 1）

2022 年，Plonky 2 发布。Plonky 2 的主要创新是对较小的素数进行模运算：2 的 64 次方 - 2 的 32 次方 + 1 = 18446744067414584321。现在，每次加法或乘法都可以在 CPU 上用几条指令完成，并且将所有数据哈希在一起的速度比以前快 4 倍。但有一个问题：这种方法仅适用于 STARK。如果您尝试使用 SNARK，那么对于如此小的椭圆曲线，椭圆曲线将变得不安全。

为了保证安全性，Plonky 2 还需要引入扩展字段。检查算术方程的一个关键技术是随机点采样：如果要检查 H(x) * Z(x) 是否等于 F(x+ 2)-F(x+ 1)-F(x)，可以随机选择一个坐标 r，提供一个多项式承诺来证明 H(r)、Z(r)、F(r)、F(r+ 1) 和 F(r+ 2)，然后验证 H(r) * Z(r) 是否等于 F(r+ 2)-F(r+ 1)-F(r)。如果攻击者可以提前猜出坐标，那么攻击者就可以欺骗证明系统 —— 这就是证明系统必须随机的原因。但这也意味着坐标必须从足够大的集合中采样，以至于攻击者无法随机猜出。如果模数接近 2 的 256 次方，这显然是正确的。但是，对于模数 2^64 – 2^32 + 1，我们还没有到达那里，如果我们降到 2^31 – 1，情况肯定不会如此。攻击者完全有能力尝试伪造证明二十亿次，直到成功为止。

为了防止这种情况发生，我们从扩展域中抽样 r，这样，例如，您可以定义 y，其中 y^3 = 5，并取 1、y 和 y^2 的组合。这使坐标总数达到约 2^93。证明者计算的大多数多项式都不会进入这个扩展域；它们只是模 2^31-1 的整数，因此您仍然可以从使用小域中获得所有效率。但随机点检查和 FRI 计算确实会进入这个更大的域以获得所需的安全性。

从小素数到二进制数

计算机通过将较大的数字表示为 0 和 1 的序列，并在这些位之上构建电路来计算加法和乘法等运算来进行算术运算。计算机特别针对 16 位、32 位和 64 位整数进行了优化。例如，选择 2^64 – 2^32 + 1 和 2^31 – 1 不仅是因为它们符合这些界限，而且因为它们很好地符合这些界限：模 2^64 – 2^32 + 1 的乘法可以通过执行常规 32 位乘法并在几个地方按位移位和复制输出来执行；本文很好地解释了一些技巧。

然而，更好的方法是直接用二进制进行计算。如果加法可以只是异或，而不必担心将 1 + 1 从一个位加到下一个位会产生结转，那会怎样？如果乘法可以以同样的方式并行化，那会怎样？这些优势都基于能够用单个位表示真/假值。

直接进行二进制计算的优势正是 Binius 想要实现的。Binius 团队在 zkSummit 的演示中展示了效率提升：

尽管大小大致相同，但对 32 位二进制字段的运算所需的计算资源比对 31 位梅森字段的运算少 5 倍。

从单变量多项式到超立方体

假设我们相信这个推理，并想用比特（0 和 1）来做所有事情。我们如何用一个多项式来表示十亿比特？

这里我们面临两个实际问题：

1. 如果多项式要表示大量的值，则在求多项式的值时，这些值必须是可访问的：在上面的斐波那契示例中，F(0)、F(1) ... F(100)，而在更大的计算中，指数将达到数百万。我们使用的字段需要包含这种大小的数字。

2. 证明我们在 Merkle 树中提交的任何值（就像所有 STARK 一样）都需要对其进行 Reed-Solomon 编码：例如，将值从 n 扩展到 8n，使用冗余来防止恶意证明者在计算过程中伪造值以作弊。这还需要有足够大的字段：要将一百万个值扩展到 8 百万个，您需要 8 百万个不同的点来评估多项式。

Binius 的一个关键思想是分别解决这两个问题，并通过以两种不同的方式表示相同的数据来实现。首先是多项式本身。基于椭圆曲线的 SNARK、2019 年的 STARK、Plonky 2 等系统通常处理一个变量的多项式：F(x)。另一方面，Binius 受到 Spartan 协议的启发，使用多元多项式：F(x 1, x 2,… xk)。实际上，我们在计算超立方体上表示整个计算轨迹，其中每个 xi 要么是 0，要么是 1。例如，如果我们想要表示斐波那契数列，并且我们仍然使用一个足够大的字段来表示它们，我们可以想象它们的前 16 个序列如下：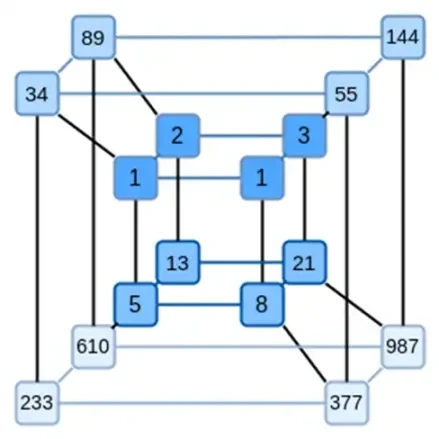

也就是说，F(0,0,0,0) 应该是 1，F(1,0,0,0) 也是 1，F(0,1,0,0) 是 2，依此类推，直到 F(1,1,1,1) = 987。给定这样一个计算超立方体，有一个多元线性（每个变量的次数为 1）多项式可以产生这些计算。因此，我们可以将这组值视为表示多项式；我们不需要计算系数。

这个例子当然只是为了说明：在实践中，进入超立方体的整个目的是让我们处理单个位。Binius 计算斐波那契数的原生方法是使用高维立方体，每组（比如说 16 位）存储一个数字。这需要一些聪明才智才能在位的基础上实现整数加法，但对于 Binius 来说，这并不太难。

现在，让我们看看纠删码。STARK 的工作方式是，你取 n 个值，Reed-Solomon 将它们扩展为更多值（通常为 8n，通常在 2n 到 32n 之间），然后从扩展中随机选择一些 Merkle 分支并对它们执行某种检查。超立方体在每个维度上的长度为 2。因此，直接扩展它是不切实际的：没有足够的空间从 16 个值中采样 Merkle 分支。那么我们怎么做呢？让我们假设超立方体是一个正方形！

简单的 Binius – 一个例子

看 这里 用于协议的python实现。

让我们看一个例子，为了方便起见，我们使用常规整数作为字段（在实际实现中，我们将使用二进制字段元素）。首先，我们将要提交的超立方体编码为正方形：

现在，我们使用 Reed-Solomon 方法展开平方。也就是说，我们将每一行视为在 x = { 0, 1, 2, 3 } 处求值的 3 次多项式，并在 x = { 4, 5, 6, 7 } 处求值相同的多项式：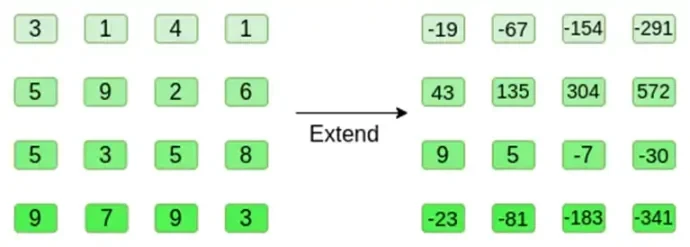

请注意，数字可能会变得非常大！这就是为什么在实际实现中我们总是使用有限域，而不是常规整数：例如，如果我们使用模 11 的整数，则第一行的展开将只是 [3, 10, 0, 6]。

如果您想尝试该扩展并亲自验证数字，您可以在此处使用我的简单 Reed-Solomon 扩展代码。

接下来，我们将这个扩展视为一个列，并创建该列的 Merkle 树。Merkle 树的根就是我们的承诺。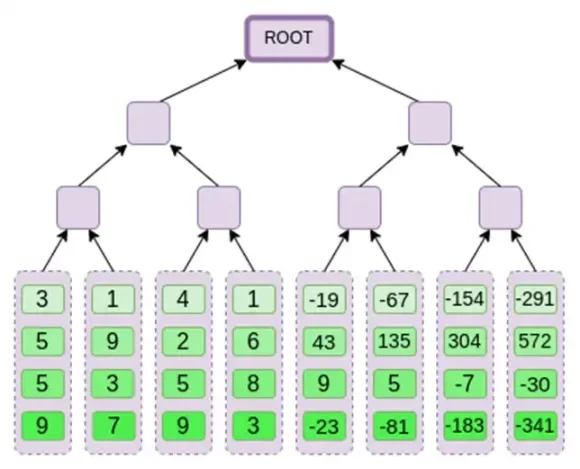

现在，让我们假设证明者想要在某个时刻证明这个多项式 r = {r 0, r 1, r 2, r 3 } 的计算。Binius 中有一个细微的差别，这使其比其他多项式承诺方案更弱：证明者在承诺 Merkle 根之前不应该知道或能够猜测 s（换句话说，r 应该是一个依赖于 Merkle 根的伪随机值）。这使得该方案对于数据库查找毫无用处（例如，好的，你给了我 Merkle 根，现在向我证明 P(0, 0, 1, 0)！）。但我们实际使用的零知识证明协议通常不需要数据库查找；它们只需要在随机评估点检查多项式。所以这个限制很好地满足了我们的目的。

假设我们选择 r = { 1, 2, 3, 4 }（多项式求值为 -137；您可以使用此代码确认这一点）。现在，我们开始证明。我们将 r 分成两部分：第一部分 { 1, 2 } 表示行内列的线性组合，第二部分 { 3, 4 } 表示行的线性组合。我们计算列的张量积和：

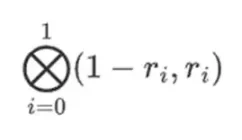
对于行部分：

这意味着：每个集合中某个值的所有可能乘积的列表。在行的情况下，我们得到：

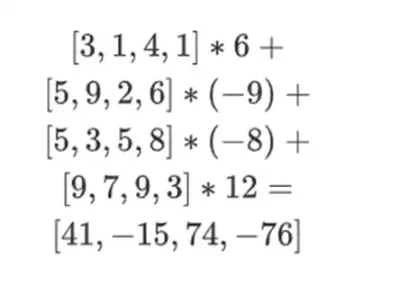
[( 1-r 2)*( 1-r 3), ( 1-r 3), ( 1-r 2)*r 3, r 2*r 3 ]

其中 r = { 1, 2, 3, 4 } （因此 r 2 = 3 且 r 3 = 4）：

[( 1-3)*( 1-4), 3*( 1-4),( 1-3)* 4, 3* 4 ] = [ 6, -9 -8 -12 ]

现在，我们通过对现有行进行线性组合来计算新行 t。也就是说，我们取：

您可以将此处发生的事情视为部分求值。如果我们将完整张量积乘以所有值的完整向量，您将得到计算 P(1, 2, 3, 4) = -137。在这里，我们仅使用一半的求值坐标乘以部分张量积，并将 N 个值的网格缩减为一行平方根 N 值。如果您将此行提供给其他人，他们可以使用另一半求值坐标的张量积完成其余计算。

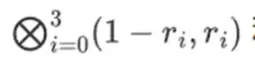
证明者向验证者提供以下新行：t 和一些随机采样列的 Merkle 证明。在我们的说明性示例中，我们将让证明者仅提供最后一列；在现实生活中，证明者需要提供数十列才能实现足够的安全性。

现在，我们利用 Reed-Solomon 码的线性。我们利用的关键特性是，对 Reed-Solomon 展开进行线性组合与对线性组合进行 Reed-Solomon 展开得到的结果相同。这种顺序独立性通常发生在两个运算都是线性的时候。

验证者正是这么做的。他们计算 t，并计算证明者之前计算过的相同列的线性组合（但仅限于证明者提供的列），并验证这两个过程是否给出相同的答案。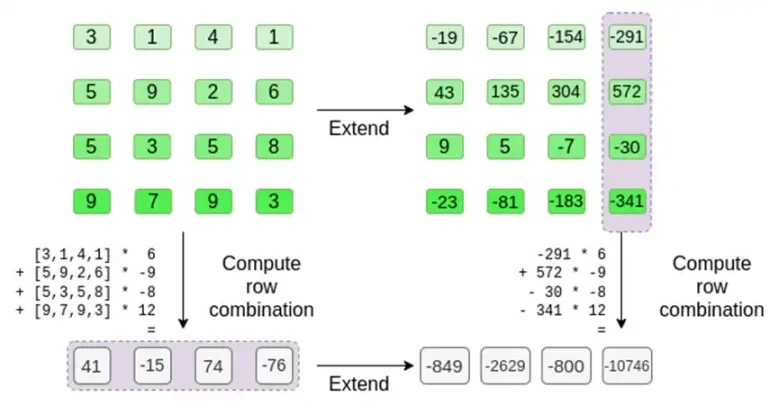

在这种情况下，我们展开 t 并计算相同的线性组合 ([6,-9,-8, 12])，它们都给出相同的答案：-10746。这证明 Merkle 根是善意构建的（或至少足够接近），并且它与 t 匹配：至少绝大多数列彼此兼容。

但验证者还需要检查一件事：检查多项式 {r 0 …r 3 } 的求值。到目前为止，验证者的所有步骤实际上都不依赖于证明者声称的值。以下是我们的检查方法。我们取标记为计算点的“列部分”的张量积：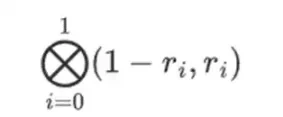

在我们的例子中，r = { 1, 2, 3, 4 }，因此选定的列的一半是 { 1, 2 })，这相当于：

现在我们取这个线性组合t：

这与直接求解多项式是一样的。

以上内容非常接近简单 Binius 协议的完整描述。这已经具有一些有趣的优势：例如，由于数据被分成行和列，因此只需要一半大小的字段。但是，这并不能实现二进制计算的全部优势。为此，我们需要完整的 Binius 协议。但首先，让我们更深入地了解二进制字段。

二进制字段

最小可能的域是模2的算术域，它非常小，我们可以为它写出加法和乘法表：

我们可以通过扩展获得更大的二进制域：如果我们从 F 2 （模 2 的整数）开始，然后定义 x 其中 x 平方 = x + 1 ，我们得到以下加法和乘法表：

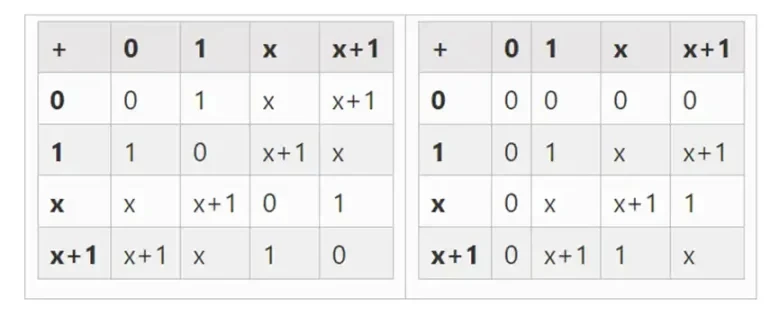
事实证明，通过重复此构造，我们可以将二进制域扩展到任意大的尺寸。与实数上的复数不同，在复数中，您可以添加新元素但永远不会再添加任何元素 I（四元数确实存在，但它们在数学上很奇怪，例如 ab 不等于 ba），而有限域可以永远添加新的扩展。具体来说，我们对元素的定义如下：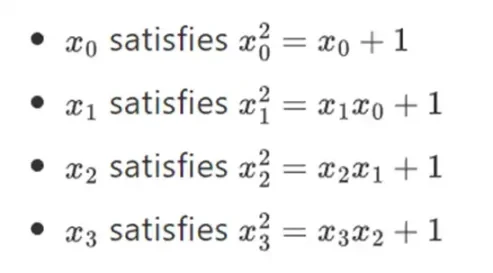

等等……这通常被称为塔式构造，因为每次连续扩展都可以被认为是在塔上添加新的一层。这不是构造任意大小的二进制字段的唯一方法，但它具有 Binius 利用的一些独特优势。

我们可以将这些数字表示为位列表。例如，1100101010001111。第一位表示 1 的倍数，第二位表示 x0 的倍数，然后以下位表示 x1 的倍数：x1、x1*x0、x2、x2*x0 等等。这种编码很好，因为您可以将其分解：

这是一种相对不常见的符号，但我喜欢将二进制域元素表示为整数，并将更高效的位放在右侧。也就是说，1 = 1、x0 = 01 = 2、1+x0 = 11 = 3、1+x0+x2 = 11001000 = 19，等等。在这个表示中，就是 61779。

二进制域中的加法只是 XOR（顺便说一下，减法也是如此）；请注意，这意味着对于任何 x，x+x = 0。要将两个元素 x*y 相乘，有一个非常简单的递归算法：将每个数字分成两半：

然后，拆分乘法：

最后一部分是唯一有点棘手的部分，因为你必须应用简化规则。有更有效的方法来做乘法，类似于 Karatsubas 算法和快速傅里叶变换，但我将把它留给感兴趣的读者作为练习。

二进制域中的除法是通过结合乘法和逆运算来完成的。简单但缓慢的逆运算方法是广义费马小定理的应用。还有一个更复杂但更高效的逆运算算法，您可以在此处找到。您可以使用此处的代码来操作二进制域的加法、乘法和除法。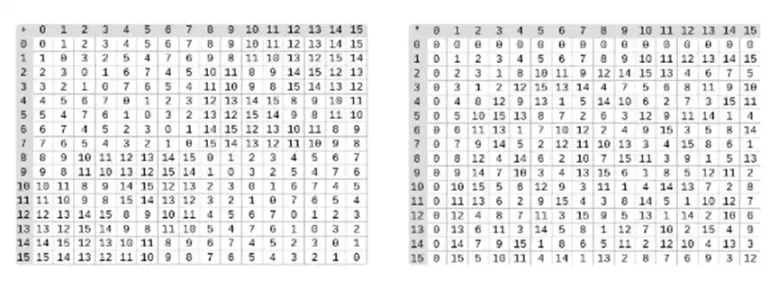

左：四位二进制域元素的加法表（即只有 1、x 0、x 1、x 0x 1）。右：四位二进制域元素的乘法表。

这种类型的二元域的美妙之处在于它结合了常规整数和模运算的一些最佳部分。与常规整数一样，二元域元素也是无界的：你可以根据需要将其增大到任意大小。但就像模运算一样，如果你对某个大小限制内的值进行运算，则所有结果都将保持在同一范围内。例如，如果你对 42 进行连续幂运算，则会得到：

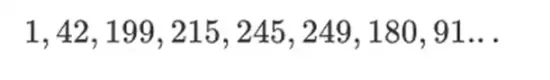
经过255步之后，你又回到了42的255次方=1，而且就像正整数和模运算一样，它们遵循通常的数学定律：a*b=b*a，a*(b+c)=a*b+a*c，甚至一些奇怪的新定律。

最后，二进制字段便于操作位：如果您使用适合 2k 的数字进行数学运算，那么您的所有输出也将适合 2k 位。这避免了尴尬。在以太坊的 EIP-4844 中，blob 的各个块必须是模 52435875175126190479447740508185965837690552500527637822603658699938581184513 的数字，因此编码二进制数据需要丢弃一些空间并在应用层进行额外检查，以确保存储在每个元素中的值小于 2248。这也意味着二进制字段操作在计算机上非常快 - 无论是 CPU 还是理论上最佳的 FPGA 和 ASIC 设计。

这一切意味着我们可以像上面那样进行 Reed-Solomon 编码，这样可以完全避免我们在示例中看到的整数爆炸，并且以非常自然的方式进行计算机擅长的计算。二进制字段的拆分属性（我们如何执行 1100101010001111 = 11001010 + 10001111*x 3 ，然后根据需要将其拆分）对于实现很大的灵活性也至关重要。

完成 Binius

看 这里 用于协议的python实现。

现在我们可以继续讨论“完整 Binius”，它改编了“简单 Binius”，以便 (i) 处理二进制域和 (ii) 让我们提交单个位。该协议很难理解，因为它在查看位矩阵的不同方式之间来回切换；我理解它所花的时间肯定比我理解加密协议所花的时间要长。但一旦你理解了二进制域，好消息是 Binius 所依赖的“更难的数学”并不存在。这不是椭圆曲线配对，那里有越来越深的代数几何兔子洞需要深入；在这里，你只有二进制域。

让我们再看一下完整的图表：

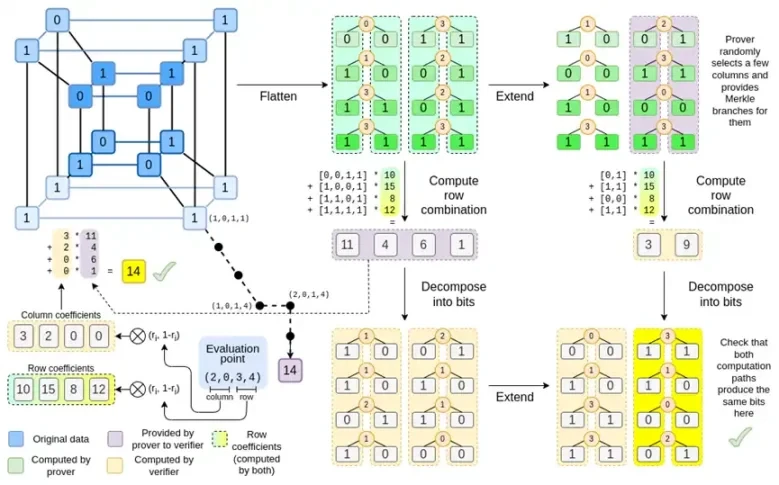
现在，您应该已经熟悉了大部分组件。将超立方体展平为网格的思想、将行和列组合计算为评估点的张量积的思想，以及检查 Reed-Solomon 展开然后计算行组合与计算行组合然后 Reed-Solomon 展开之间的等价性的思想，都是在普通的 Binius 中实现的。

Complete Binius 有什么新功能？基本上有三件事：

• 超立方体和正方形中的各个值必须是位（0 或 1）。

• 扩展过程通过将位分组到列中并暂时假设它们是更大字段的元素来将位扩展为更多位。

• 在行组合步骤之后，还有一个逐元素分解为位的步骤，将扩展转换回位。

我们将依次讨论这两种情况。首先，新的扩展程序。Reed-Solomon 码有一个根本的限制，如果要将 n 扩展为 k*n，则需要在一个具有 k*n 个不同值的域中工作，这些值可用作坐标。使用 F 2（又名位），您不能这样做。所以我们要做的是，将 F 2 的相邻元素打包在一起以形成更大的值。在此处的示例中，我们一次将两位打包到元素 { 0 , 1 , 2 , 3 } 中，这对我们来说已经足够了，因为我们的扩展只有四个计算点。在真正的证明中，我们可能会一次返回 16 位。然后，我们对这些打包的值执行 Reed-Solomon 码并将它们再次解包为位。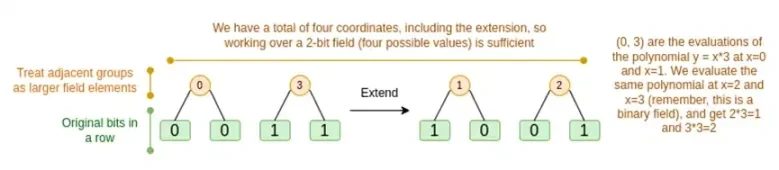

现在，行组合。为了使随机点的评估在密码学上是安全的，我们需要从相当大的空间（比超立方体本身大得多）对该点进行采样。因此，虽然超立方体内的点是位，但超立方体外的计算值将大得多。在上面的例子中，行组合最终为 [11, 4, 6, 1]。

这就带来了一个问题：我们知道如何将位分组为一个更大的值，然后对该值执行 Reed-Solomon 扩展，但我们如何对更大的值对执行同样的事情呢？

Binius 技巧是一点一点地进行：我们查看每个值的单个位（例如，对于我们标记为 11 的东西，即 [1, 1, 0, 1]），然后逐行展开。也就是说，我们在每个元素的第 1 行上展开它，然后在 x0 行上展开，然后在 x1 行上展开，然后在 x0x1 行上展开，依此类推（好吧，在我们的玩具示例中我们停在那里，但在实际实现中我们会扩展到 128 行（最后一行是 x6*…*x0））

审查：

• 我们将超立方体中的位转换为网格

• 然后，我们将每行相邻位的组视为更大域的元素，并对它们执行算术运算以 Reed-Solomon 扩展行

• 然后，我们取每列位的行组合，并得到每行的位列作为输出（对于大于 4 x 4 的正方形，输出要小得多）

• 然后，我们将输出视为一个矩阵，并将其位视为行

为什么会发生这种情况？在普通数学中，如果你开始逐位切分一个数字，那么以任何顺序进行线性运算并获得相同结果的（通常）能力就会失效。例如，如果我从数字 345 开始，然后将其乘以 8，然后乘以 3，我得到 8280，如果我反向执行这两个操作，我也会得到 8280。但如果我在这两个步骤之间插入一个位切分操作，它就会失效：如果你先执行 8x，然后执行 3x，你会得到：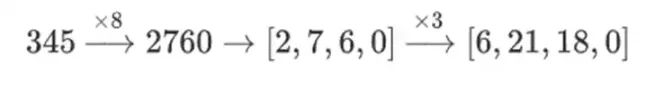

但如果你做 3 倍，然后 8 倍，你会得到：

但在用塔式结构构建的二元域中，这种方法确实有效。原因在于它们的可分离性：如果你将一个大值乘以一个小值，那么每个段上发生的事情将保留在每个段上。如果我们将 1100101010001111 乘以 11，这与 1100101010001111 的第一次分解相同，即

然后将每个组件乘以 11。

综合起来

一般来说，零知识证明系统通过对多项式做出陈述来工作，这些陈述同时代表了对底层评估的陈述：就像我们在斐波那契示例中看到的那样，F(X+ 2)-F(X+ 1)-F(X) = Z(X)*H(X)，同时检查斐波那契计算的所有步骤。我们通过在随机点处证明评估来检查多项式的陈述。对随机点的检查代表了对整个多项式的检查：如果多项式方程不匹配，则在特定的随机坐标处匹配的可能性很小。

实际上，效率低下的一个主要原因是，在实际程序中，我们处理的大多数数字都很小：for 循环中的索引、真/假值、计数器等等。但是，当我们使用 Reed-Solomon 编码扩展数据以提供使基于 Merkle 证明的检查安全所需的冗余时，大多数额外的值最终会占据整个字段的大小，即使原始值很小。

为了解决这个问题，我们希望使这个字段尽可能小。Plonky 2 将数字从 256 位数提高到 64 位数，然后 Plonky 3 将其进一步降低到 31 位。但即使这样也不是最佳选择。使用二进制字段，我们可以处理单个位。这使得编码变得密集：如果您的实际基础数据有 n 位，那么您的编码将有 n 位，扩展将有 8*n 位，没有额外的开销。

现在，让我们第三次看一下该图表：

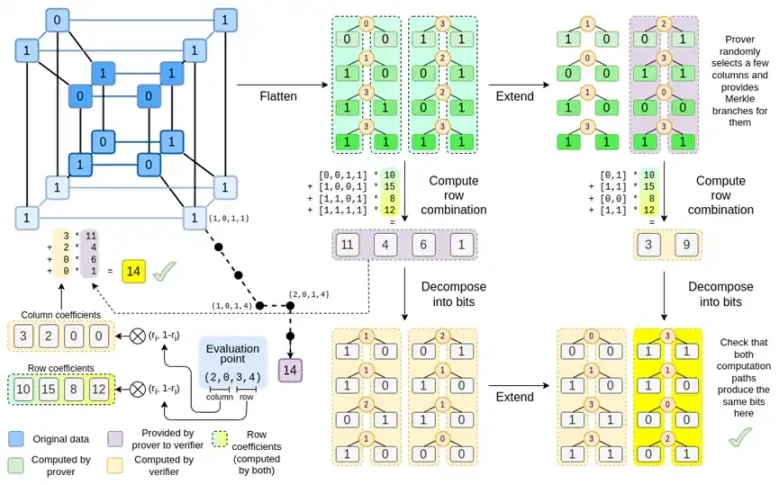
在 Binius 中，我们研究一个多线性多项式：超立方体 P(x0, x1,…xk)，其中单个评估 P(0, 0, 0, 0)、P(0, 0, 0, 1) 直到 P(1, 1, 1, 1)，保存着我们关心的数据。为了在某个点证明计算结果，我们将相同的数据重新解释为一个正方形。然后，我们使用 Reed-Solomon 编码扩展每一行，以提供抵御随机 Merkle 分支查询所需的数据冗余。然后，我们计算行的随机线性组合，设计系数，以便新的组合行实际上包含我们关心的计算值。这个新创建的行（重新解释为 128 位行）和一些带有 Merkle 分支的随机选择的列将传递给验证者。

然后，验证者执行扩展行组合（或更准确地说，扩展列）和扩展行组合，并验证两者是否匹配。然后，它计算列组合并检查它是否返回证明者声称的值。这就是我们的证明系统（或更准确地说，多项式承诺方案，它是证明系统的关键组成部分）。

我们还没有涉及什么？

• 需要一种有效的算法来扩展行，才能真正提高验证器的计算效率。我们对二进制字段使用快速傅里叶变换，如本文所述（尽管确切的实现会有所不同，因为这篇文章使用了一种效率较低的、不基于递归扩展的构造）。

• 从算术角度来看。单变量多项式很方便，因为您可以执行诸如 F(X+2)-F(X+1)-F(X) = Z(X)*H(X) 之类的操作来链接计算中的相邻步骤。在超立方体中，下一步的解释远不如 X+1 清楚。您可以执行 X+k，k 的幂，但这种跳跃行为牺牲了 Binius 的许多关键优势。Binius 论文描述了解决方案。参见第 4.3 节），但这本身就是一个很深的兔子洞。

• 如何安全地进行特定值检查。斐波那契示例需要检查关键边界条件：F(0)=F(1)=1 和 F(100) 的值。但对于原始 Binius，在已知计算点进行检查是不安全的。有一些相当简单的方法可以将已知计算检查转换为未知计算检查，使用所谓的总和检查协议；但我们不会在这里介绍这些。

• 查找协议是最近广泛使用的另一项技术，用于构建超高效的证明系统。Binius 可与查找协议结合用于许多应用程序。

• 超越平方根验证时间。平方根非常昂贵：2^32 位的 Binius 证明大约有 11 MB 长。您可以使用其他证明系统来制作 Binius 证明的证明，从而以较小的证明大小获得 Binius 证明的效率。另一个选择是更复杂的 FRI-Binius 协议，它创建多对数大小的证明（就像常规 FRI 一样）。

• Binius 如何影响 SNARK 友好性。基本总结是，如果您使用 Binius，您就不再需要关心如何使计算对算术友好：常规哈希不再比传统算术哈希更有效，模 2 的 32 次方或模 2 的 256 次方乘法不再像模 2 乘法那么痛苦，等等。但这是一个复杂的话题。当一切都以二进制完成时，很多事情都会发生变化。

我希望在未来几个月内看到基于二进制字段的证明技术的更多改进。

本文来源于网络：Vitalik: Binius，二元域的高效证明

相关：BNB 币显示出复苏迹象：有望创下年度新高

简言之，BNB 价格从 $550 反弹，接近突破 $593 阻力位。价格指标已恢复看涨势头，支持 8% 上涨。夏普比率为 4.03，可能会推动新投资者转向交易所代币。3 月对 BNB 币来说是一个有利的月份，该加密货币在短短几天内创下了今年的两个新高，然后经历了一次回调。经过近两周的复苏期，BNB 币显示出可能在 2024 年创下新高的迹象。但这样的里程碑可以实现吗？BNB 看起来很有希望在从 $550 支撑位反弹后，BNB 币的价值在本次分析时已升至 $581。这一改善反映了山寨币风险回报状况的恢复，……