Vitalik：Binius，二進位字段的高效證明

原文作者：Vitalik Buterin

原文翻譯：Kate，MarsBit

這篇文章主要針對熟悉 2019 時代密碼學，特別是 SNARK 和 STARK 的讀者。如果您不是，我建議您先閱讀這些內容。特別感謝 Justin Drake、Jim Posen、Benjamin Diamond 和 Radi Cojbasic 的回饋和評論。

在過去的兩年裡，STARK 已經成為一種關鍵且不可替代的技術，可以有效地為非常複雜的語句提供易於驗證的加密證明（例如證明以太坊區塊是有效的）。造成這種情況的關鍵原因之一是字段大小較小：基於橢圓曲線的 SNARK 要求您處理 256 位元整數才能足夠安全，而 STARK 允許您以更高的效率使用更小的字段大小：首先是 Goldilocks 字段（64 位元整數），然後是Mersenne 31 和BabyBear（都是31 位元）。由於這些效率提升，使用 Goldilocks 的 Plonky 2 在證明多種計算方面比其前身快數百倍。

一個自然的問題是：我們能否將這一趨勢推向邏輯結論，並透過直接對零和一進行操作來建立運行速度更快的證明系統？這正是 Binius 試圖要做的，使用了許多數學技巧，使其與三年前的 SNARK 和 STARK 有很大不同。這篇文章描述了為什麼小字段使證明生成更加高效，為什麼二進位字段具有獨特的強大功能，以及 Binius 用於使二進製字段證明如此高效的技巧。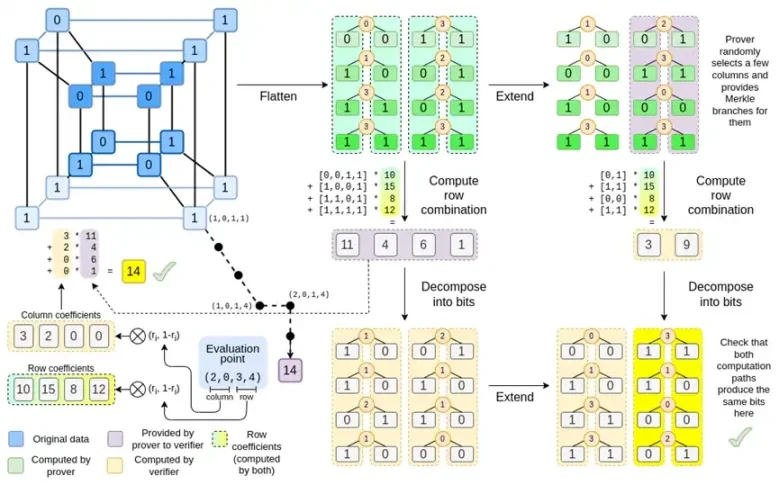

Binius，在這篇文章結束時，您應該能夠理解該圖的每個部分。

回顧：有限域

密碼證明系統的關鍵任務之一是在保持少量資料的同時對大量資料進行操作。如果您可以將有關大型程式的語句壓縮為包含幾個數字的數學方程，但這些數字與原始程式一樣大，那麼您將一無所獲。

為了在保持較小數字的同時進行複雜算術，密碼學家通常使用模算術。我們選擇一個質數模 p。 % 運算子表示取餘數：15% 7 = 1、53% 10 = 3，依此類推。 （請注意，答案始終為非負數，例如 -1% 10 = 9）

您可能看過加減時間的模算術（例如，現在是 9 點後 4 小時是幾點？）。但在這裡，我們不只是對數字進行加法和減法；而是對數字進行加法和減法。我們也可以乘法、除法和取指數。

我們重新定義：

上述規則都是自洽的。例如，如果 p = 7，則：

5 + 3 = 1（因為 8% 7 = 1）

1-3 = 5（因為-2% 7 = 5）

2* 5 = 3

3/5 = 2

這種結構的更通用術語是有限域。有限域是一種遵循通常算術定律的數學結構，但其中可能值的數量是有限的，因此每個值都可以用固定大小表示。

模算術（或質數域）是最常見的有限域類型，但還有另一種類型：擴展域。您可能已經看過一個擴充欄位：複數。我們想像一個新元素並將其標記為 i，並用它進行數學運算：(3i+2)*(2i+4)=6i*i+12i+4i+8=16i+2。我們可以對素數域的擴展做同樣的事情。當我們開始處理較小的字段時，素數字段的擴展對於安全性變得越來越重要，而二進位字段（Binius 使用的）完全依賴擴展來具有實用性。

複習：算術化

SNARK 和 STARK 證明電腦程式的方式是透過算術：您取得有關要證明的程式的陳述，並將其轉換為涉及多項式的數學方程式。方程式的有效解對應於程式的有效執行。

舉一個簡單的例子，假設我計算了第 100 個斐波那契數，我想向你證明它是什麼。我建立了一個對斐波那契數列進行編碼的多項式F：因此F(0)=F(1)=1、F(2)=2、F(3)=3、F(4)=5 等等，共100 步。我需要證明的條件是在整個範圍x={0, 1…98}上F(x+2)=F(x)+F(x+1)。我可以透過給你商來說服你：

其中 Z(x) = (x-0) * (x-1) * …(x-98)。 。如果我能提供F和H滿足這個方程，那麼F必須在範圍內滿足F(x+ 2)-F(x+ 1)-F(x)。如果我另外驗證對於 F，F(0)=F(1)=1，那麼 F(100) 其實一定是第 100 個斐波那契數。

如果你想證明更複雜的東西，那麼你可以用一個更複雜的方程式來取代簡單的關係F(x+2) = F(x) + F(x+1)，該方程式基本上表示F(x+ 1) 是輸出初始化具有狀態 F(x) 的虛擬機，並執行一個計算步驟。您還可以將數字 100 替換為更大的數字，例如 100000000，以容納更多步驟。

所有 SNARK 和 STARK 都基於使用多項式（有時是向量和矩陣）上的簡單方程式來表示各個值之間的大量關係的想法。並非所有演算法都像上面那樣檢查相鄰計算步驟之間的等效性：例如，PLONK 不會，R1CS 也不會。但許多最有效的檢查都會這樣做，因為透過多次執行相同的檢查（或相同的少數檢查）可以更輕鬆地最小化開銷。

Plonky 2：從 256 位元 SNARK 和 STARK 到 64 位元…僅 STARK

五年前，不同類型的零知識證明的合理總結如下。有兩種類型的證明：（基於橢圓曲線的）SNARK 和（基於哈希的）STARK。從技術上講，STARK 是 SNARK 的一種，但在實踐中，通常使用“SNARK”來指基於橢圓曲線的變體，使用“STARK”來指基於哈希的構造。 SNARK 很小，因此您可以非常快速地驗證它們並輕鬆將它們安裝到鏈上。 STARK 很大，但它們不需要可信設置，而且具有量子抗性。

STARK 的工作原理是將數據視為多項式，計算該多項式的計算結果，並使用擴展數據的 Merkle 根作為「多項式承諾」。

這裡的一個關鍵歷史是基於橢圓曲線的 SNARKs 首先被廣泛使用：由於 FRI，STARKs 直到 2018 年左右才變得足夠高效，那時 Zcash 已經運行了一年多。基於橢圓曲線的 SNARK 有一個關鍵限制：如果您想使用基於橢圓曲線的 SNARK，則這些方程中的算術必須以橢圓曲線上的點數為模進行。這是一個很大的數字，通常接近2 的256 次方：例如，對於bn128 曲線，它是2188824287183927522224640574525727508854836440041603434369585最喜歡的語言編寫的真實程序，其中大部分內容用途包括計數器、for 迴圈中的索引、程式中的位置、表示 True 或 False 的單一位元以及其他幾乎總是只有幾個數字長度的東西。

即使您的原始數據由少量數字組成，證明過程也需要計算商、擴展、隨機線性組合和其他數據轉換，這些數據轉換將產生相同或更多數量的對象，這些對象的平均大小與您的原始數據的完整大小一樣大。這造成了一個關鍵的低效率問題：為了證明對 n 個小值的計算，您必須對 n 個大得多的值進行更多計算。最初，STARK 繼承了 SNARK 使用 256 位元欄位的習慣，因此也遭受了同樣的低效率。

一些多項式評估的 Reed-Solomon 展開。即使原始值很小，附加價值也會擴展到欄位的完整大小（在本例中為 2^31 – 1）

2022 年，Plonky 2 發布。 Plonky 2 的主要創新是對較小素數進行算術運算：2 的 64 次方 – 2 的 32 次方 + 1 = 18446744067414584321。的速度比以前快4 倍。但有一個問題：這種方法只適用於 STARK。如果您嘗試使用 SNARK，那麼對於如此小的橢圓曲線，橢圓曲線就會變得不安全。

為了確保安全性，Plonky 2還需要引入擴充欄位。檢查算術方程式的一個關鍵技術是隨機點採樣：如果要檢查 H(x) * Z(x) 是否等於 F(x+ 2)-F(x+ 1)-F(x)，可以隨機進行選擇一個座標r ，提供多項式承諾來證明H(r)、Z(r)、F(r)、F(r+ 1)和F(r+ 2)，然後驗證是否H(r) * Z(r ) 等於F(r+ 2 )-F(r+ 1)- F(r)。如果攻擊者可以提前猜出座標，那麼攻擊者就可以欺騙證明系統——這就是為什麼證明系統必須是隨機的。但這也意味著必須從足夠大的集合中採樣座標，以使攻擊者無法隨機猜測。如果模數接近 2 的 256 次方，這顯然是正確的。 31 – 1. 攻擊者完全有能力嘗試偽造證明20 億次，直到幸運為止。

為了防止這種情況，我們從擴展字段中對 r 進行採樣，例如，您可以定義 y，其中 y^3 = 5，並採用 1、y 和 y^2 的組合。這使得座標總數達到大約 2^93。證明者計算的多項式大多不屬於這個擴展域；它們只是以 2^31-1 為模的整數，因此您仍然可以透過使用小字段來獲得所有效率。但隨機點檢查和 FRI 計算確實進入了這個更大的領域，以獲得他們所需的安全性。

從小質數到二進制數

計算機透過將較大的數字表示為 0 和 1 的序列，並在這些位元之上建構電路來計算加法和乘法等運算來進行算術運算。計算機特別針對 16 位元、32 位元和 64 位元整數進行了最佳化。例如，選擇 2^64 – 2^32 + 1 和 2^31 – 1 不僅是因為它們適合這些邊界，還因為它們很好地適合這些邊界：乘法模 2^64 – 2^32 + 1可以透過進行常規32 位元乘法、按位移位並在幾個位置複製輸出來執行；這篇文章很好地解釋了一些技巧。

然而，更好的方法是直接以二進制形式進行計算。如果加法可以只是異或，而不必擔心將 1 + 1 從一位添加到下一位而產生的結轉會怎麼樣？如果乘法可以以同樣的方式更加並行化呢？這些優點都是基於能夠用單位元表示真/假值。

要獲得直接進行二進位運算的這些優勢正是 Binius 正在嘗試做的事情。 Binius 團隊在 zkSummit 的演講中展現了效率提升：

儘管大小大致相同，但 32 位元二進位欄位上的操作所需的計算資源比 31 位元 Mersenne 欄位上的操作少 5 倍。

從單變量多項式到超立方體

假設我們相信這個推理，並且想要用位子（0 和 1）做所有事情。我們如何用一個多項式表示十億位元？

這裡我們面臨兩個實際問題：

1. 對於表示大量值的多項式，在計算多項式時需要可存取這些值：在上面的斐波那契範例中，F(0)、F(1) … F(100)，以及在更大的計算中，指數將以百萬為單位。我們使用的欄位需要包含此大小的數字。

2. 證明我們在Merkle 樹（像所有STARK 一樣）中提交的任何值都需要對其進行Reed-Solomon 編碼：例如，將值從n 擴展到8n，使用冗餘來防止惡意證明者在計算過程中透過偽造值進行作弊。這也需要有一個足夠大的欄位：要從 100 萬個值擴展到 800 萬個，您需要 800 萬個不同的點來評估多項式。

Binius 的一個關鍵想法是分別解決這兩個問題，並透過以兩種不同的方式表示相同的資料來實現。首先，多項式本身。基於橢圓曲線的 SNARK、2019 時代的 STARK、Plonky 2 等系統通常處理一個變數上的多項式：F(x)。另一方面，Binius 從 Spartan 協議中汲取靈感，並使用多元多項式：F(x 1, x 2,… xk)。實際上，我們在計算超立方體上表示整個計算軌跡，其中每個xi 要么是0，要么是1。 ，我們可以想像他們的前 16 個序列是這樣的：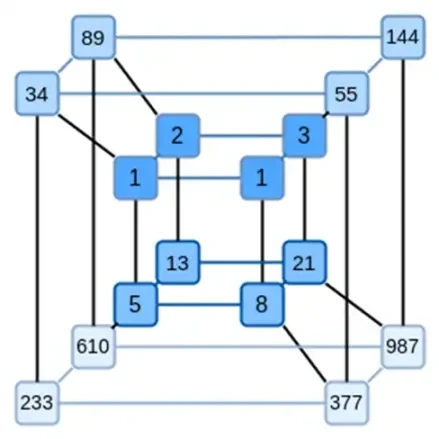

即 F(0,0,0,0) 應該是 1，F(1,0,0,0) 也是 1，F(0,1,0,0) 是 2，以此類推，所有直到F(1 ,1,1,1) = 987。所以我們可以認為這組值代表多項式；我們不需要計算係數。

這個例子當然只是為了說明：在實踐中，進入超立方體的全部目的是讓我們處理各個位元。 Binius 計算斐波那契數的原生方法是使用高維立方體，每組（例如 16 位元）儲存一個數字。這需要一些聰明才智來實現基於位的整數加法，但對於 Binius 來說，這並不太難。

現在，讓我們來看看糾刪碼。 STARK 的工作方式是，你取n 個值，Reed-Solomon 將它們擴展為更多值（通常為8n，通常在2n 到32n 之間），然後從擴展中隨機選擇一些Merkle 分支並對它們執行某種檢查。超立方體的每個維度的長度都是 2。因此，直接擴展它是不切實際的：沒有足夠的空間來從 16 個值中取樣 Merkle 分支。那我們該怎麼做呢？讓我們假設超立方體是一個正方形！

簡單的 Binius——一個例子

看 這裡 該協定的 python 實作。

讓我們看一個範例，為了方便起見，使用常規整數作為欄位（在實際實作中，我們使用二進位欄位元素）。首先，我們將要提交的超立方體編碼為正方形：

現在，我們使用里德-所羅門方法展開方形。也就是說，我們將每一行視為在 x = { 0, 1, 2, 3 } 處計算的 3 次多項式，並在 x = { 4, 5, 6, 7 } 處計算相同的多項式：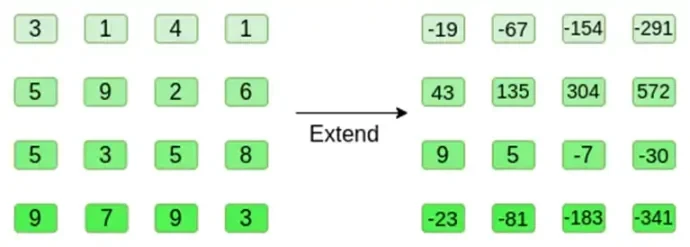

請注意，數字可能會變得非常大！這就是為什麼在實際實作中我們總是使用有限域，而不是常規整數：例如，如果我們使用以 11 為模的整數，則第一行的擴展將只是 [3, 10, 0, 6]。

如果您想嘗試擴展並親自驗證號碼，您可以在此處使用我的簡單的里德所羅門擴展代碼。

接下來，我們將此擴充視為一列，並建立該列的 Merkle 樹。 Merkle 樹的根是我們的承諾。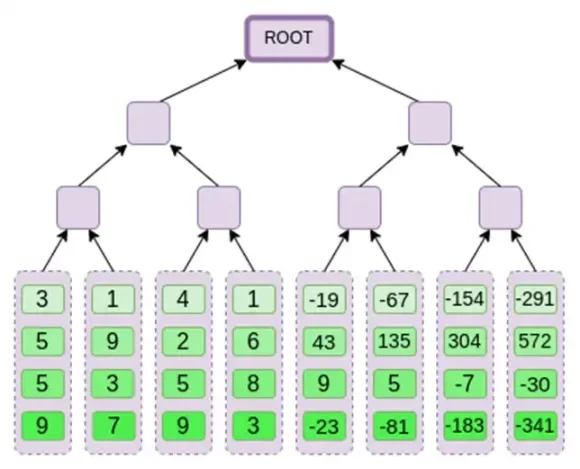

現在，假設證明者想要在某個時刻證明該多項式 r = {r 0, r 1, r 2, r 3 } 的計算。 Binius 有一個微妙的差異，這使得它比其他多項式承諾方案更弱：證明者在提交 Merkle 根之前不應該知道或能夠猜測 s（換句話說，r 應該是一個偽隨機值，取決於默克爾根）。這使得該方案對於資料庫查找毫無用處（例如，好吧，你給了我 Merkle 根，現在向我證明 P(0, 0, 1, 0)！）。但我們實際使用的零知識證明協議通常不需要資料庫查找；它們只需要在隨機評估點檢查多項式。所以這個限制很好地滿足了我們的目的。

假設我們選擇 r = { 1, 2, 3, 4 } （多項式的計算結果為 -137；您可以使用此程式碼確認這一點）。現在，我們來證明一下。我們將 r 分成兩部分：第一部分 { 1, 2 } 表示行內列的線性組合，第二部分 {3, 4 } 表示行的線性組合。我們計算列的張量積：

對於行部分：

這意味著：每組中某個值的所有可能乘積的清單。在行的情況下，我們得到：

[(1-r 2)*(1-r 3),(1-r 3),(1-r 2)*r 3,r 2*r 3 ]

當 r = { 1, 2, 3, 4 } （因此 r 2 = 3 且 r 3 = 4）：

[( 1-3)*( 1-4), 3*( 1-4),( 1-3)* 4, 3* 4 ] = [ 6, -9 -8 -12 ]

現在，我們透過現有行的線性組合來計算新行 t。也就是說，我們取：

您可以將此處發生的情況視為部分評估。如果我們將全張量乘積乘以所有值的全向量，您將得到計算結果 P(1, 2, 3, 4) = -137。在這裡，我們僅使用一半的評估座標來乘以部分張量積，並將 N 個值的網格縮減為單行平方根 N 個值。如果您將此行交給其他人，他們可以使用另一半評估座標的張量積來完成其餘的計算。

證明者向驗證者提供以下新行：t 和一些隨機採樣列的 Merkle 證明。在我們的說明範例中，我們將讓證明者只提供最後一列；在現實生活中，證明者需要提供數十個欄位才能達到足夠的安全性。

現在，我們利用里德-所羅門碼的線性。我們利用的關鍵特性是，採用里德-所羅門展開式的線性組合與採用線性組合的里德-所羅門展開式得到相同的結果。當兩個運算都是線性時，通常會發生這種順序獨立性。

驗證者正是這麼做的。他們計算 t，併計算證明者之前計算的相同列的線性組合（但僅限證明者提供的列），並驗證兩個過程給出相同的答案。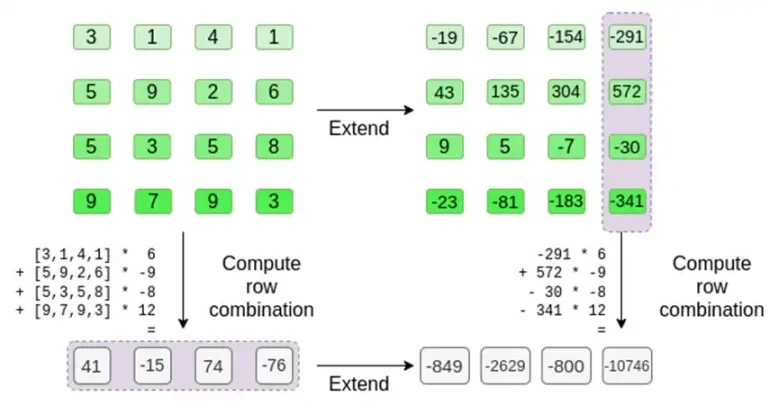

在這種情況下，我們展開 t 併計算相同的線性組合 ([6,-9,-8, 12])，它們都給出相同的答案：-10746。這證明 Merkle 根是善意構建的（或至少足夠接近），並且它與 t 匹配：至少絕大多數列彼此兼容。

但驗證者還需要檢查一件事：檢查多項式 {r 0 …r 3 } 的評估。到目前為止，驗證者的所有步驟實際上並不依賴證明者聲稱的值。這是我們檢查的方法。我們取標記為計算點的「列部分」的張量積：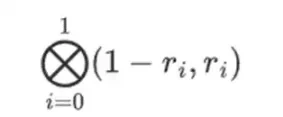

在我們的例子中，其中 r = { 1, 2, 3, 4 }，因此所選列的一半是 { 1, 2 })，這相當於：

現在我們採用這個線性組合 t：

這與直接求解多項式相同。

以上非常接近簡單 Binius 協議的完整描述。這已經具有一些有趣的優點：例如，由於資料被分為行和列，因此您只需要一個大小一半的欄位。然而，這並沒有實現二進制計算的全部好處。為此，我們需要完整的 Binius 協定。但首先，讓我們更深入地了解二進位字段。

二進位字段

最小的可能字段是算術模 2，它是如此之小，以至於我們可以為其編寫加法和乘法表：

我們可以透過擴展得到更大的二進位字段：如果我們從 F 2 （整數模 2）開始，然後定義 x，其中 x 平方 = x + 1 ，我們得到以下加法和乘法表：

事實證明，我們可以透過重複這種構造將二進位字段擴展到任意大的大小。與實數上的複數不同，您可以添加一個新元素，但永遠不會添加任何更多元素I（四元數確實存在，但它們在數學上很奇怪，例如ab 不等於ba），對於有限域，您可以添加新的擴充永遠。具體來說，我們對元素的定義如下：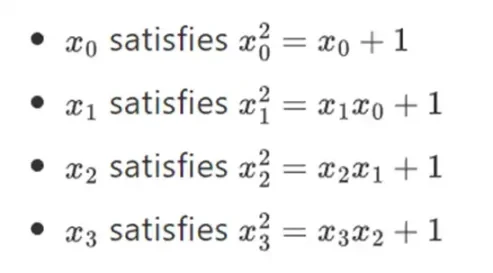

等等……這通常被稱為塔樓建設，因為每次連續的擴建都可以被認為是為塔樓添加了一個新的層。這不是構造任意大小的二進位字段的唯一方法，但它具有 Binius 所利用的一些獨特優勢。

我們可以將這些數字表示為位元列表。例如，1100101010001111。這種編碼很好，因為你可以分解它：

這是一種相對不常見的表示法，但我喜歡將二進位字段元素表示為整數，並且更有效的位元位於右側。即，1 = 1、x0 = 01 = 2、1+x0 = 11 = 3、1+x0+x2 = 11001000 = 19，依此類推。在此表示法中，即 61779。

二進位字段中的加法只是異或（順便說一句，減法也是如此）；請注意，這意味著對於任何 x，x+x = 0。要將兩個元素 x*y 相乘，有一個非常簡單的遞歸演算法：將每個數字分成兩半：

然後，拆分乘法：

最後一部分是唯一有點棘手的部分，因為您必須應用簡化規則。有更有效的方法來進行乘法，類似於 Karatsubas 演算法和快速傅立葉變換，但我將把它作為練習，讓有興趣的讀者弄清楚。

二進位域中的除法是透過組合乘法和反轉來完成的。簡單但緩慢的反演方法是廣義費馬小定理的應用。您還可以在此處找到更複雜但更有效的反演演算法。您可以使用此處的程式碼來處理二進位欄位的加法、乘法和除法。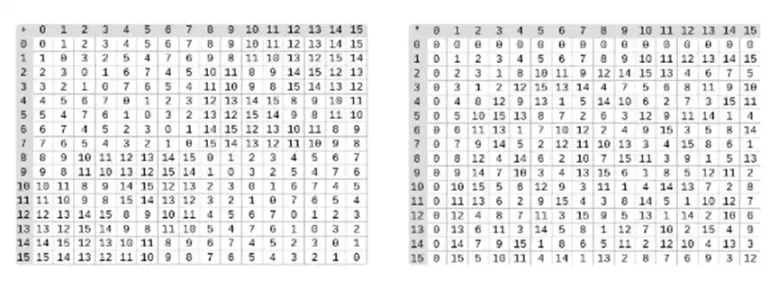

左：四位元二進位欄位元素的加法表（即只有 1、x 0、x 1、x 0x 1）。右：四位二進位字段元素的乘法表。

這種類型的二進位字段的優點在於它結合了常規整數和模算術的一些最好的部分。與常規整數一樣，二進位字段元素是無界的：您可以隨心所欲地增長。但就像模運算一樣，如果您對特定大小限制內的值進行運算，則所有結果都將保持在同一範圍內。例如，如果您取 42 的連續冪，您將得到：

255 步之後，你又回到了 42 的 255 次方 = 1，就像正整數和模運算一樣，它們遵循通常的數學定律：a*b=b*a, a*(b+c)= a* b+a*c，甚至還有一些奇怪的新定律。

最後，二進位欄位對於操作位元很方便：如果您使用適合 2k 位元的數字進行數學運算，那麼所有輸出也將適合 2k 位元。這樣就避免了尷尬。在以太坊 EIP-4844 中，blob 的各個區塊必須以 52435875175126190479447740508185965837690552500527637822603658691938525005276378226036586993853869115381913658699385每個元素中儲存的值小於 2248。著二進位字段運算在電腦上非常快——無論是CPU 還是理論上最佳的FPGA 和ASIC 設計。

這一切都意味著我們可以像上面那樣進行Reed-Solomon 編碼，以一種完全避免整數爆炸的方式，正如我們在示例中看到的那樣，並且以一種非常原生的方式，這是計算機擅長的計算類型。二進位欄位的拆分屬性（我們如何執行 1100101010001111 = 11001010 + 10001111*x 3 ，然後根據需要將其拆分）對於實現很大的靈活性也至關重要。

完成比尼烏斯

看 這裡 該協定的 python 實作。

現在我們可以繼續討論“完整的 Binius”，它採用“簡單的 Binius”來（i）處理二進位字段以及（ii）讓我們提交單個位元。該協議很難理解，因為它在查看位元矩陣的不同方式之間來回切換；我理解它所花費的時間肯定比我通常理解加密協議所花費的時間要長。但是，一旦您了解了二進位字段，好消息是 Binius 所依賴的「更難的數學」並不存在。這不是橢圓曲線配對，那裡有越來越深的代數幾何兔子洞需要深入。在這裡，你只有二進位字段。

讓我們再看一下完整的圖表：

到目前為止，您應該熟悉大多數組件。將超立方體展平為網格的想法，計算行和列組合作為評估點的張量積的想法，以及檢查里德-所羅門展開然後計算行組合和計算行組合然後里德-所羅門展開之間的等價性的想法都是在普通的 Binius 中實現的。

Complete Binius 有什麼新功能？基本上三件事：

• 超立方體和平方中的各個值必須是位（0 或 1）。

• 擴展過程透過將位元分組為列並暫時假設它們是更大字段的元素來將位元擴展為更多位元。

• 在行組合步驟之後，有一個按元素分解為位元的步驟，將擴充轉換回位元。

我們依序討論這兩種情況。首先，新的延期程序。 Reed-Solomon 碼有一個基本限制，如果要將 n 擴展到 k*n，則需要在具有 k*n 個可用作座標的不同值的欄位中工作。對於 F 2 （又稱位元），你無法做到這一點。所以我們要做的就是將 F 2 的相鄰元素打包在一起以形成更大的值。在這裡的範例中，我們一次將兩個位元打包到元素 { 0 , 1 , 2 , 3 } 中，這對我們來說已經足夠了，因為我們的擴充只有四個計算點。在真正的證明中，我們可能一次返回 16 位元。然後，我們對這些打包值執行 Reed-Solomon 程式碼，並將它們再次解包為位元。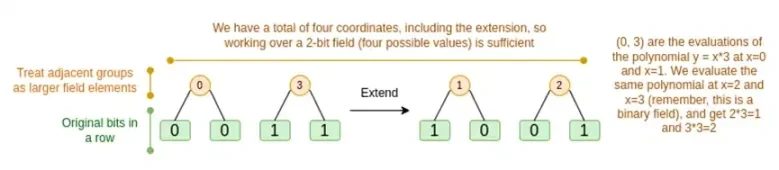

現在，行組合。為了使隨機點的評估在加密上安全，我們需要從相當大的空間（比超立方體本身大得多）中對該點進行採樣。因此，雖然超立方體內部的點是位，但超立方體外部的計算值會大得多。在上面的範例中，行組合最終為 [11, 4, 6, 1]。

這就提出了一個問題：我們知道如何將位元分組為一個更大的值，然後對該值執行里德所羅門擴展，但是我們如何對更大的值對做同樣的事情呢？

Binius 技巧是一點一點地做到這一點：我們查看每個值的一位（例如，對於我們標記為11 的東西，即[1, 1, 0, 1]），然後我們逐行展開它。也就是說，我們將其展開到每個元素的第1 行，然後展開到x0 行，然後展開到x1 行，然後展開到x0x1 行，依此類推（好吧，在我們的玩具示例中我們就到此為止，但在真實的情況下）實現最多 128 行（最後一行是 x6*…*x0））

審查：

• 我們將超立方體中的位元轉換為網格

• 然後，我們將每行上的相鄰位元組視為更大字段的元素，並對它們執行算術運算以 Reed-Solomon 擴展該行

• 然後，我們取得每列位元的行組合，並將每行的位元列作為輸出（對於大於 4 x 4 的正方形要小得多）

• 然後，我們將輸出視為矩陣，將其位元視為行

為什麼會發生這種情況？在普通數學中，如果您開始一點一點地對數字進行切片，那麼以任何順序進行線性運算並獲得相同結果的（通常）能力就會崩潰。例如，如果我從數字 345 開始，將其乘以 8，然後乘以 3，我得到 8280，如果我反向執行這兩個操作，我也會得到 8280。個步驟之間，它會崩潰：如果你執行8x，然後執行3x，你會得到：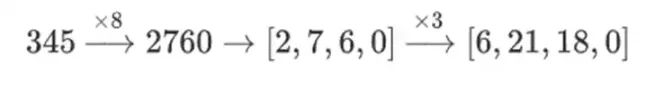

但如果你先做 3 次，然後再做 8 次，你會得到：

但在用塔式結構建造的二元領域中，這種方法確實有效。原因是它們的可分離性：如果將一個大值乘以一個小值，則每個段落上發生的事情都會保留在每個段落上。如果我們將 1100101010001111 乘以 11，這與 1100101010001111 的第一次分解相同，即

然後將每個分量乘以 11。

把它們放在一起

一般來說，零知識證明系統的工作原理是對多項式進行陳述，同時表示有關底層評估的陳述：就像我們在斐波那契示例中看到的那樣，F(X+ 2)-F(X+ 1 )-F( X) = Z(X)*H(X) 同時檢查斐波那契計算的所有步驟。我們透過證明隨機點的評估來檢查有關多項式的陳述。對隨機點的檢查代表整個多項式的檢查：如果多項式方程式不匹配，則它在特定隨機座標處匹配的可能性很小。

在實踐中，效率低下的一個主要原因是，在實際程序中，我們處理的大多數數字都很小：for 迴圈中的索引、True/False 值、計數器等等。然而，當我們使用 Reed-Solomon 編碼擴展資料以提供確保基於 Merkle 證明的檢查安全所需的冗餘時，大多數額外值最終會佔據欄位的整個大小，即使原始值很小。

為了解決這個問題，我們希望使該字段盡可能小。 Plonky 2 將我們從 256 位數字帶到了 64 位數字，然後 Plonky 3 進一步將其降至 31 位。但即使這樣也不是最佳的。使用二進位字段，我們可以處理單一位元。這使得編碼變得密集：如果你的實際底層資料有 n 位，那麼你的編碼將有 n 位，擴展將有 8*n 位，沒有額外的開銷。

現在，讓我們第三次看一下這張圖表：

在 Binius 中，我們研究多重線性多項式：超立方體 P(x0, x1,…xk)，其中單一評估 P(0, 0, 0, 0), P(0, 0, 0, 1) 直至 P( 1 ,1,1,1)，保存我們關心的資料。為了證明某一點的計算，我們將相同的數據重新解釋為正方形。然後，我們使用 Reed-Solomon 編碼擴展每一行，以提供針對隨機 Merkle 分支查詢的安全性所需的資料冗餘。然後，我們計算行的隨機線性組合，設計係數，以便新的組合行實際上包含我們關心的計算值。這個新建立的行（重新解釋為 128 位元行）和一些隨機選擇的帶有 Merkle 分支的列被傳遞給驗證者。

然後驗證器執行擴展行組合（或更準確地說，擴展列）和擴展行組合併驗證兩者是否匹配。然後，它計算列組合併檢查它是否傳回證明者聲明的值。這就是我們的證明系統（或更準確地說，多項式承諾方案，它是證明系統的關鍵組成部分）。

我們還沒討論什麼？

• 需要一種有效的演算法來擴展行，才能真正提高驗證器的計算效率。我們在二進位字段上使用快速傅立葉變換，如此處所述（儘管確切的實現會有所不同，因為本文使用了不基於遞歸擴展的效率較低的構造）。

• 從算術上來說。單變量多項式很方便，因為您可以執行F(X+2)-F(X+1)-F(X) = Z(X)*H(X) 之類的操作來連結計算中的相鄰步驟。在超立方體中，下一步的解釋遠不如 X+1 好。您可以執行 X+k，k 的冪，但這種跳躍行為犧牲了 Binius 的許多關鍵優勢。 Binius 論文描述了解決方案。請參閱第 4.3 節），但這本身就是一個很深的兔子洞。

• 如何安全地進行特定值檢查。斐波那契範例需要檢查關鍵邊界條件：F(0)=F(1)=1 和 F(100) 的值。但對於原來的Binius來說，在已知的計算點做檢查是不安全的。有一些相當簡單的方法可以使用所謂的和檢查協議將已知計算檢查轉換為未知計算檢查；但我們不會在這裡討論這些。

• 查找協議是最近廣泛使用的另一種技術，用於建立超高效的證明系統。 Binius 可以與許多應用程式的查找協定結合使用。

• 超出平方根驗證時間。平方根的成本很高：2^32 位元的 Binius 證明大約有 11 MB 長。您可以透過使用其他證明系統來進行 Binius 證明的證明來彌補這一點，從而以較小的證明大小提供 Binius 證明的效率。另一種選擇是更複雜的 FRI-Binius 協議，它創建多對數大小的證明（就像常規 FRI 一樣）。

• Binius 如何影響 SNARK 友善性。基本總結是，如果您使用 Binius，您不再需要關心計算是否適合算術：常規哈希不再比傳統算術哈希、模 2 的 32 次方乘法或模 2 的 32 次方更有效率。像模2 乘法等那樣痛苦。當一切都以二進位完成時，很多事情都會改變。

我期望在未來幾個月看到基於二進位字段的證明技術的更多改進。

本文源自網路：Vitalik：Binius，二進位域的高效率證明

相關：BNB 幣顯示復甦跡象：新高即將到來

簡而言之，BNB 價格從 $550 反彈，接近突破 $593 阻力位。價格指標重新恢復看漲勢頭，支撐8%上漲。 4.03 的夏普比率可能會推動新投資者轉向交易所代幣。 3 月對 BNB 幣來說是一個有利的月份，該加密貨幣在短短幾天內就創下了年內的兩個新高，然後經歷了調整。經過近兩週的恢復期，BNB Coin顯示出有可能在2024年創下新高的跡象。 BNB 看起來很有前途 在從 $550 支撐位反彈後，BNB 幣的價值在本次分析時已升至 $581。這項改善反映了山寨幣風險回報狀況的復甦，…