Vitalik: Binius، بائنری فیلڈز کے لیے موثر ثبوت

اصل مضمون بذریعہ: وٹالِک بوٹیرن

اصل ترجمہ: کیٹ، مارس بٹ

یہ پوسٹ بنیادی طور پر ان قارئین کے لیے ہے جو عام طور پر 2019 کے دور کی خفیہ نگاری، اور خاص طور پر SNARKs اور STARKs سے واقف ہیں۔ اگر آپ نہیں ہیں تو، میں ان کو پہلے پڑھنے کی تجویز کرتا ہوں۔ جسٹن ڈریک، جم پوسن، بینجمن ڈائمنڈ، اور ریڈی کوجبیسک کا ان کے تاثرات اور تبصروں کے لیے خصوصی شکریہ۔

پچھلے دو سالوں کے دوران، STARKs انتہائی پیچیدہ بیانات (مثلاً یہ ثابت کرنا کہ Ethereum بلاک درست ہے) کے آسانی سے قابل تصدیق کرپٹوگرافک ثبوتوں کو مؤثر طریقے سے بنانے کے لیے ایک اہم اور ناقابل تبدیلی ٹیکنالوجی بن گئی ہے۔ اس کی ایک اہم وجہ فیلڈ کا چھوٹا سائز ہے: بیضوی منحنی خطوط پر مبنی SNARKs کے لیے آپ کو 256 بٹ انٹیجرز پر کام کرنے کی ضرورت ہوتی ہے تاکہ آپ کافی محفوظ رہیں، جب کہ STARKs آپ کو زیادہ کارکردگی کے ساتھ بہت چھوٹے فیلڈ سائز استعمال کرنے کی اجازت دیتے ہیں: پہلے Goldilocks فیلڈ (64 بٹ انٹیجر)، پھر مرسین 31 اور بیبی بیئر (دونوں 31 بٹس)۔ کارکردگی کے ان فوائد کی وجہ سے، گولڈی لاکس کا استعمال کرتے ہوئے Plonky 2 کئی قسم کے حسابات کو ثابت کرنے میں اپنے پیشروؤں سے سینکڑوں گنا تیز ہے۔

ایک فطری سوال یہ ہے کہ: کیا ہم اس رجحان کو منطقی انجام تک پہنچا سکتے ہیں اور ایسے پروف سسٹم بنا سکتے ہیں جو براہ راست زیرو اور ون پر کام کر کے تیزی سے چلتے ہیں؟ یہ بالکل وہی ہے جو Binius کرنے کی کوشش کرتا ہے، بہت سے ریاضیاتی چالوں کا استعمال کرتے ہوئے جو اسے تین سال پہلے کے SNARKs اور STARKs سے بہت مختلف بناتا ہے۔ اس پوسٹ میں بتایا گیا ہے کہ چھوٹے فیلڈز پروف جنریشن کو زیادہ موثر کیوں بناتے ہیں، بائنری فیلڈز منفرد طور پر طاقتور کیوں ہیں، اور بائنری فیلڈز پر ثبوت بنانے کے لیے بائنیئس کی چالیں اتنی موثر کیوں ہیں۔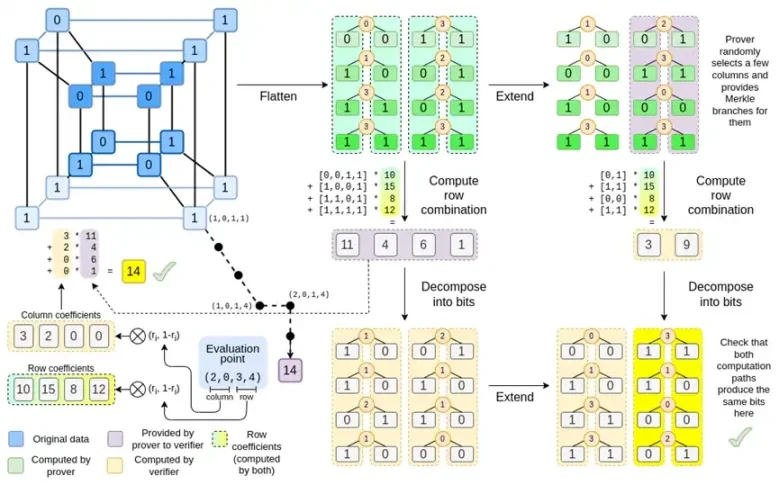

Binius، اس پوسٹ کے اختتام تک، آپ کو اس خاکہ کے ہر حصے کو سمجھنے کے قابل ہونا چاہیے۔

جائزہ: محدود فیلڈز

کرپٹوگرافک پروف سسٹمز کے اہم کاموں میں سے ایک یہ ہے کہ اعداد کو چھوٹا رکھتے ہوئے بڑی مقدار میں ڈیٹا پر کام کیا جائے۔ اگر آپ کسی بڑے پروگرام کے بارے میں بیان کو چند نمبروں پر مشتمل ریاضیاتی مساوات میں کمپریس کر سکتے ہیں، لیکن وہ تعداد اصل پروگرام کی طرح بڑی ہیں، تو آپ کو کچھ حاصل نہیں ہوا۔

اعداد کو چھوٹا رکھتے ہوئے پیچیدہ ریاضی کرنے کے لیے، کرپٹوگرافر اکثر ماڈیولر ریاضی کا استعمال کرتے ہیں۔ ہم ایک پرائم نمبر ماڈیولس پی کا انتخاب کرتے ہیں۔ % آپریٹر کا مطلب ہے کہ بقیہ لیں: 15% 7 = 1، 53% 10 = 3، وغیرہ۔ (نوٹ کریں کہ جواب ہمیشہ غیر منفی ہوتا ہے، اس لیے مثال کے طور پر -1% 10 = 9)

آپ نے ماڈیولر ریاضی کو وقت جوڑنے اور گھٹانے کے تناظر میں دیکھا ہوگا (مثال کے طور پر، 9 کے بعد 4 گھنٹے کیا وقت ہے؟)۔ لیکن یہاں، ہم صرف ایک عدد کو شامل اور گھٹاتے نہیں ہیں۔ ہم ضرب، تقسیم، اور اخراج کو بھی لے سکتے ہیں۔

ہم دوبارہ وضاحت کرتے ہیں: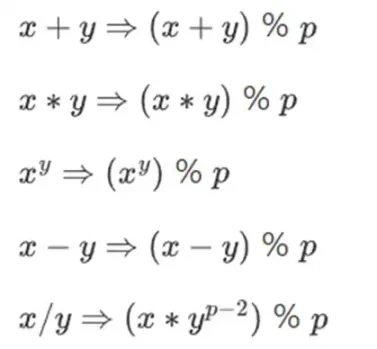

مندرجہ بالا قوانین تمام خود موافق ہیں۔ مثال کے طور پر، اگر p = 7، تو:

5 + 3 = 1 (کیونکہ 8% 7 = 1)

1-3 = 5 (کیونکہ -2% 7 = 5)

2* 5 = 3

3/5 = 2

اس طرح کے ڈھانچے کے لئے ایک زیادہ عام اصطلاح محدود فیلڈز ہے۔ ایک محدود فیلڈ ایک ریاضیاتی ڈھانچہ ہے جو ریاضی کے معمول کے قوانین کی پیروی کرتا ہے، لیکن جس میں ممکنہ قدروں کی تعداد محدود ہے، تاکہ ہر قدر کو ایک مقررہ سائز سے ظاہر کیا جا سکے۔

ماڈیولر ریاضی (یا پرائم فیلڈز) محدود فیلڈ کی سب سے عام قسم ہے، لیکن ایک اور قسم ہے: ایکسٹینشن فیلڈز۔ آپ نے ایک ایکسٹینشن فیلڈ دیکھا ہوگا: پیچیدہ نمبرز۔ ہم ایک نئے عنصر کا تصور کرتے ہیں اور اسے i کا لیبل لگاتے ہیں، اور اس کے ساتھ ریاضی کرتے ہیں: (3i+2)*(2i+4)=6i*i+12i+4i+8=16i+2۔ ہم پرائم فیلڈ کی توسیع کے ساتھ بھی ایسا ہی کر سکتے ہیں۔ جیسا کہ ہم چھوٹے شعبوں کے ساتھ کام کرنا شروع کرتے ہیں، پرائم فیلڈز کی توسیع سیکیورٹی کے لیے تیزی سے اہم ہوتی جاتی ہے، اور بائنری فیلڈز (Binius کے ذریعے استعمال کیے جاتے ہیں) عملی افادیت کے لیے مکمل طور پر توسیع پر انحصار کرتے ہیں۔

جائزہ: ریاضی

جس طرح سے SNARKs اور STARKs کمپیوٹر پروگراموں کو ثابت کرتے ہیں وہ ریاضی کے ذریعے ہے: آپ جس پروگرام کو ثابت کرنا چاہتے ہیں اس کے بارے میں ایک بیان لیتے ہیں، اور اسے ایک ریاضیاتی مساوات میں تبدیل کرتے ہیں جس میں ایک کثیر نام شامل ہوتا ہے۔ مساوات کا ایک درست حل پروگرام کے درست عمل کے مساوی ہے۔

ایک سادہ مثال کے طور پر، فرض کریں کہ میں نے 100ویں فبونیکی نمبر کا حساب لگایا اور میں آپ کو ثابت کرنا چاہتا ہوں کہ یہ کیا ہے۔ میں ایک کثیر نام F بناتا ہوں جو فبونیکی ترتیب کو انکوڈ کرتا ہے: تو F(0)=F(1)=1، F(2)=2، F(3)=3، F(4)=5 اور اسی طرح 100 مراحل کے لیے . مجھے ثابت کرنے کی شرط یہ ہے کہ F(x+2)=F(x)+F(x+1) پوری رینج x={0, 1…98} پر۔ میں آپ کو حصّہ دے کر قائل کر سکتا ہوں:

جہاں Z(x) = (x-0) * (x-1) * … (x-98)۔ . اگر میں فراہم کر سکتا ہوں کہ F اور H اس مساوات کو پورا کرتے ہیں، تو F کو F(x+ 2)-F(x+ 1)-F(x) کو حد میں پورا کرنا چاہیے۔ اگر میں اضافی طور پر تصدیق کرتا ہوں کہ F، F(0)=F(1)=1، تو F(100) درحقیقت 100 واں فبونیکی نمبر ہونا چاہیے۔

اگر آپ کچھ زیادہ پیچیدہ ثابت کرنا چاہتے ہیں، تو آپ سادہ رشتہ F(x+2) = F(x) + F(x+1) کو ایک زیادہ پیچیدہ مساوات سے بدل دیتے ہیں جو بنیادی طور پر کہتا ہے کہ F(x+1) آؤٹ پٹ ہے۔ اسٹیٹ F(x) کے ساتھ ایک ورچوئل مشین کو شروع کرنے، اور ایک کمپیوٹیشنل مرحلہ چلائیں۔ مزید مراحل کو ایڈجسٹ کرنے کے لیے آپ نمبر 100 کو بڑی تعداد سے بھی بدل سکتے ہیں، مثال کے طور پر، 100000000۔

تمام SNARKs اور STARKs انفرادی اقدار کے درمیان بڑی تعداد میں رشتوں کی نمائندگی کرنے کے لیے کثیر الجہتی (اور بعض اوقات ویکٹر اور میٹرکس) پر سادہ مساوات کو استعمال کرنے کے خیال پر مبنی ہیں۔ تمام الگورتھم اوپر کی طرح ملحقہ کمپیوٹیشنل مراحل کے درمیان مساوات کی جانچ نہیں کرتے ہیں: مثال کے طور پر، PLONK نہیں کرتا، اور نہ ہی R1CS کرتا ہے۔ لیکن بہت سے مؤثر چیک ایسا کرتے ہیں، کیونکہ ایک ہی چیک (یا وہی چند چیک) کئی بار کر کے اوور ہیڈ کو کم کرنا آسان ہوتا ہے۔

Plonky 2: 256-bit SNARKs اور STARKs سے 64-bit… صرف STARKs

پانچ سال پہلے، مختلف قسم کے صفر علمی ثبوتوں کا ایک معقول خلاصہ حسب ذیل تھا۔ ثبوت کی دو قسمیں ہیں: (بیضوی وکر پر مبنی) SNARKs اور (ہیش پر مبنی) STARKs۔ تکنیکی طور پر، STARKs SNARK کی ایک قسم ہیں، لیکن عملی طور پر، یہ عام بات ہے کہ "SNARK" کو بیضوی وکر کی بنیاد پر اور ہیش پر مبنی تعمیر کا حوالہ دینے کے لیے "STARK" کا استعمال کیا جاتا ہے۔ SNARKs چھوٹے ہوتے ہیں، اس لیے آپ ان کی بہت جلد تصدیق کر سکتے ہیں اور انہیں آسانی سے آن چین انسٹال کر سکتے ہیں۔ STARKs بڑے ہوتے ہیں، لیکن انہیں قابل اعتماد سیٹ اپ کی ضرورت نہیں ہوتی، اور وہ کوانٹم مزاحم ہوتے ہیں۔

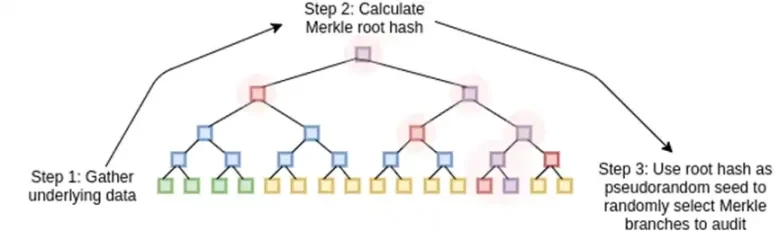
STARKs ڈیٹا کو ایک کثیر الثانی کے طور پر دیکھ کر، اس کثیر الثانی کی گنتی کا حساب لگا کر، اور توسیع شدہ ڈیٹا کے مرکل روٹ کو بطور "کثیراتی عزم" استعمال کر کے کام کرتے ہیں۔

یہاں کی تاریخ کا ایک اہم ٹکڑا یہ ہے کہ بیضوی وکر پر مبنی SNARKs کو پہلے بڑے پیمانے پر استعمال کیا گیا تھا: FRI کی بدولت 2018 کے آس پاس STARKs کافی کارآمد نہیں ہوئے تھے، اور اس وقت تک Zcash ایک سال سے چل رہا تھا۔ بیضوی وکر پر مبنی SNARKs کی ایک اہم حد ہوتی ہے: اگر آپ بیضوی وکر پر مبنی SNARK استعمال کرنا چاہتے ہیں، تو ان مساواتوں میں ریاضی کو بیضوی منحنی خطوط پر پوائنٹس کی تعداد کے مطابق کیا جانا چاہیے۔ یہ ایک بڑی تعداد ہے، جو عام طور پر 256 کی طاقت کے قریب ہوتی ہے: مثال کے طور پر، bn128 وکر کے لیے یہ 218882428718392752222464057452572750885483644004160343436968475 کا اصلی نمبر استعمال کرتا ہے۔ : اگر آپ اپنی پسندیدہ زبان میں کسی حقیقی پروگرام کے بارے میں سوچتے ہیں، تو زیادہ تر چیزیں استعمال کاؤنٹر، لوپس کے لیے اشاریہ جات، پروگرام میں پوزیشنز، سچ یا غلط کی نمائندگی کرنے والے سنگل بٹس، اور دوسری چیزیں جو تقریبا ہمیشہ صرف چند ہندسوں کی ہوتی ہیں۔

یہاں تک کہ اگر آپ کا اصل ڈیٹا چھوٹی تعداد پر مشتمل ہے، تو ثبوت کے عمل کے لیے کمپیوٹنگ کوٹینٹ، توسیع، بے ترتیب لکیری امتزاج، اور ڈیٹا کی دیگر تبدیلیوں کی ضرورت ہوتی ہے جس کے نتیجے میں اشیاء کی اتنی ہی یا بڑی تعداد ہوتی ہے جو اوسطاً اتنی بڑی ہوتی ہے جتنی کہ آپ کے پورے سائز کے۔ میدان اس سے ایک کلیدی نا اہلی پیدا ہوتی ہے: n چھوٹی قدروں پر حساب کو ثابت کرنے کے لیے، آپ کو n بہت بڑی قدروں پر بہت زیادہ کمپیوٹیشن کرنا ہوں گے۔ ابتدائی طور پر، STARKs کو 256 بٹ فیلڈز استعمال کرنے کی SNARK عادت وراثت میں ملی، اور اس طرح وہ اسی ناکارہیت کا شکار ہوئے۔

Reed-Solomon کچھ کثیر الثانی تشخیص کی توسیع۔ اگرچہ اصل قدر چھوٹی ہے، اضافی اقدار کو فیلڈ کے پورے سائز تک بڑھایا جاتا ہے (اس صورت میں 2^31 - 1)

2022 میں، پلونکی 2 ریلیز ہوئی۔ Plonky 2 کی اہم اختراع ریاضی کے ماڈیول کو ایک چھوٹا پرائم نمبر کرنا ہے: 2 سے 64 کی طاقت - 2 کی طاقت سے 32 + 1 = 18446744067414584321۔ اب، ہر ایک اضافہ یا ضرب ہمیشہ چند ہدایات میں کیا جا سکتا ہے۔ CPU، اور تمام ڈیٹا کو ایک ساتھ ہیش کرنا پہلے سے 4 گنا تیز ہے۔ لیکن ایک مسئلہ ہے: یہ طریقہ صرف اسٹارکس کے لیے کام کرتا ہے۔ اگر آپ SNARKs استعمال کرنے کی کوشش کرتے ہیں تو بیضوی منحنی خطوط ایسے چھوٹے بیضوی منحنی خطوط کے لیے غیر محفوظ ہو جاتے ہیں۔

سیکورٹی کو یقینی بنانے کے لیے، Plonky 2 کو ایکسٹینشن فیلڈز بھی متعارف کرانے کی ضرورت ہے۔ ریاضی کی مساوات کو جانچنے کے لیے ایک اہم تکنیک بے ترتیب نقطہ نمونہ ہے: اگر آپ یہ دیکھنا چاہتے ہیں کہ آیا H(x) * Z(x) F(x+ 2)-F(x+ 1)-F(x) کے برابر ہے، تو آپ تصادفی طور پر کر سکتے ہیں۔ ایک کوآرڈینیٹ r کا انتخاب کریں، H(r)، Z(r)، F(r)، F(r+1) اور F(r+2) کو ثابت کرنے کے لیے ایک کثیر الثانی عہد فراہم کریں، اور پھر تصدیق کریں کہ آیا H(r) * Z(r) ) F(r+2)-F(r+1)- F(r) کے برابر ہے۔ اگر حملہ آور نقاط کا پہلے سے اندازہ لگا سکتا ہے، تو حملہ آور پروف سسٹم کو دھوکہ دے سکتا ہے – اس لیے پروف سسٹم کو بے ترتیب ہونا چاہیے۔ لیکن اس کا مطلب یہ بھی ہے کہ نقاط کو کافی بڑے سیٹ سے نمونہ لیا جانا چاہیے جس کا حملہ آور تصادفی طور پر اندازہ نہ لگا سکے۔ یہ واضح طور پر درست ہے اگر ماڈیولس 256 کی طاقت کے 2 کے قریب ہو۔ تاہم، ماڈیولس 2^64 - 2^32 + 1 کے لیے، ہم ابھی وہاں نہیں ہیں، اور اگر ہم نیچے آتے ہیں تو یہ یقینی طور پر ایسا نہیں ہے۔ 2^31 - 1. یہ حملہ آور کی صلاحیتوں کے اندر ہے کہ وہ دو ارب بار ثبوت بنانے کی کوشش کرے جب تک کہ کوئی خوش قسمت نہ ہو۔

اس کو روکنے کے لیے، ہم ایک توسیع شدہ فیلڈ سے r کا نمونہ لیتے ہیں، تاکہ، مثال کے طور پر، آپ y کی وضاحت کر سکتے ہیں جہاں y^3 = 5، اور 1، y، اور y^2 کا مجموعہ لے سکتے ہیں۔ اس سے نقاط کی کل تعداد تقریباً 2^93 ہو جاتی ہے۔ پروور کے ذریعہ شمار کیے گئے زیادہ تر کثیر الاضلاع اس توسیعی فیلڈ میں نہیں جاتے ہیں۔ یہ صرف انٹیجرز ماڈیول 2^31-1 ہیں، لہذا آپ کو پھر بھی ایک چھوٹی فیلڈ استعمال کرنے سے تمام تر کارکردگی مل جاتی ہے۔ لیکن بے ترتیب پوائنٹ چیک اور ایف آر آئی کمپیوٹیشنز اس بڑے فیلڈ میں پہنچتے ہیں تاکہ ان کی ضرورت کی حفاظت حاصل کی جا سکے۔

چھوٹے پرائم نمبرز سے بائنری نمبرز تک

کمپیوٹر بڑی تعداد کو 0s اور 1s کی ترتیب کے طور پر پیش کر کے ریاضی کرتے ہیں، اور ان بٹس کے اوپر سرکٹس بنا کر اضافہ اور ضرب جیسے کاموں کی گنتی کرتے ہیں۔ کمپیوٹرز خاص طور پر 16-، 32-، اور 64-بٹ انٹیجرز کے لیے موزوں ہیں۔ مثال کے طور پر، 2^64 – 2^32 + 1 اور 2^31 – 1 کا انتخاب نہ صرف اس لیے کیا گیا کہ وہ ان حدود کے اندر فٹ ہوتے ہیں، بلکہ اس لیے بھی کہ وہ ان حدود کے اندر اچھی طرح فٹ ہوتے ہیں: ضرب ماڈیولو 2^64 – 2^32 + 1 ایک باقاعدہ 32 بٹ ضرب کرکے، اور کچھ جگہوں پر آؤٹ پٹ کو تھوڑا سا شفٹنگ اور کاپی کرکے انجام دیا جاسکتا ہے۔ یہ مضمون کچھ چالوں کی اچھی طرح وضاحت کرتا ہے۔

تاہم، زیادہ بہتر طریقہ یہ ہوگا کہ حسابات کو براہ راست بائنری میں کیا جائے۔ کیا ہوگا اگر اضافہ صرف XOR ہو سکتا ہے، ایک بٹ سے دوسرے میں 1 + 1 کو شامل کرنے سے لے جانے کے بارے میں فکر کیے بغیر؟ کیا ہوگا اگر ضرب اسی طرح مزید متوازی ہوسکتی ہے؟ یہ تمام فوائد ایک بٹ کے ساتھ صحیح/غلط اقدار کی نمائندگی کرنے کے قابل ہونے پر مبنی ہیں۔

براہ راست بائنری کمپیوٹیشن کرنے کے یہ فوائد حاصل کرنا بالکل وہی ہے جو بائنیئس کرنے کی کوشش کر رہا ہے۔ Binius ٹیم نے zkSummit میں اپنی پیشکش میں کارکردگی کے فوائد کا مظاہرہ کیا:

تقریباً ایک ہی سائز کے ہونے کے باوجود، 32-بٹ بائنری فیلڈز پر آپریشنز کے لیے 31-بٹ مرسین فیلڈز پر آپریشنز کے مقابلے میں 5 گنا کم کمپیوٹیشنل وسائل درکار ہوتے ہیں۔

غیر متغیر کثیر الثانیات سے ہائپر کیوبس تک

فرض کریں کہ ہم اس استدلال پر یقین رکھتے ہیں، اور سب کچھ بٹس (0 اور 1) کے ساتھ کرنا چاہتے ہیں۔ ہم ایک واحد کثیر نام کے ساتھ ایک ارب بٹس کی نمائندگی کیسے کر سکتے ہیں؟

یہاں ہمیں دو عملی مسائل کا سامنا ہے:

1. کثیر تعداد میں قدروں کی نمائندگی کرنے کے لیے، کثیر نام کی تشخیص کرتے وقت ان اقدار کو قابل رسائی ہونا ضروری ہے: اوپر دی گئی فبونیکی مثال میں، F(0)، F(1) … F(100)، اور ایک بڑے حساب میں , exponents لاکھوں میں ہوں گے. ہم جن فیلڈز کا استعمال کرتے ہیں اس سائز کے نمبروں پر مشتمل ہونا ضروری ہے۔

2. کسی بھی قدر کو ثابت کرنے کے لیے جو ہم مرکل کے درخت میں کرتے ہیں (جیسے تمام STARKs) اس کے لیے Reed-Solomon کو انکوڈنگ کی ضرورت ہوتی ہے: مثال کے طور پر، قدروں کو n سے 8n تک پھیلانا، فالتو پن کا استعمال کرتے ہوئے نقصان دہ ثابت کرنے والوں کو حساب کتاب کے دوران جعلسازی کے ذریعے دھوکہ دہی سے روکنے کے لیے۔ اس کے لیے کافی بڑا فیلڈ ہونا بھی ضروری ہے: ایک ملین ویلیو سے 8 ملین تک پھیلنے کے لیے، آپ کو کثیر الثانی کا اندازہ کرنے کے لیے 8 ملین مختلف پوائنٹس کی ضرورت ہے۔

Binius کا ایک اہم خیال یہ ہے کہ ان دونوں مسائل کو الگ الگ حل کیا جائے، اور ایک ہی ڈیٹا کو دو مختلف طریقوں سے پیش کرکے ایسا کریں۔ سب سے پہلے، polynomials خود. بیضوی منحنی خطوط پر مبنی SNARKs، 2019-era STARKs، Plonky 2، اور دیگر جیسے نظام عام طور پر ایک متغیر سے زیادہ کثیر الثانیات سے نمٹتے ہیں: F(x)۔ دوسری طرف، Binius، سپارٹن پروٹوکول سے تحریک لیتا ہے اور ملٹی ویریٹیٹ کثیر الثانیات استعمال کرتا ہے: F(x 1, x 2,… xk)۔ درحقیقت، ہم حساب کے ایک ہائپر کیوب پر پورے کمپیوٹیشنل رفتار کی نمائندگی کرتے ہیں، جہاں ہر xi یا تو 0 یا 1 ہے۔ مثال کے طور پر، اگر ہم فبونیکی ترتیب کی نمائندگی کرنا چاہتے ہیں، اور ہم پھر بھی ان کی نمائندگی کے لیے کافی بڑا فیلڈ استعمال کرتے ہیں، تو ہم کر سکتے ہیں۔ ان کے پہلے 16 سلسلے کا اس طرح تصور کریں: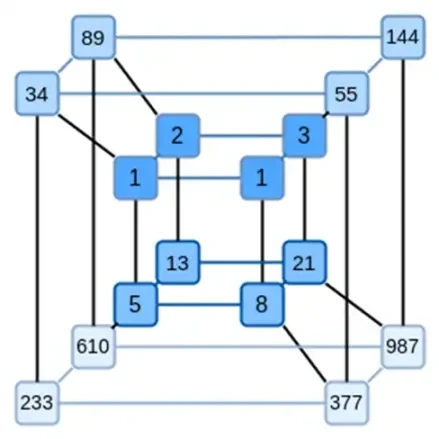

یعنی، F(0,0,0,0) 1 ہونا چاہیے، F(1,0,0,0) بھی 1، F(0,1,0,0) 2 ہے، اور اسی طرح، تمام F(1,1,1,1) = 987 تک کا راستہ۔ حسابات کے اس طرح کے ہائپر کیوب کو دیکھتے ہوئے، ایک ملٹی ویریٹیٹ لکیری (ہر متغیر میں ڈگری 1) کثیر الجہتی ہے جو یہ حسابات تیار کرتا ہے۔ لہذا ہم اقدار کے اس سیٹ کے بارے میں سوچ سکتے ہیں کہ وہ کثیر الثانی کی نمائندگی کرتا ہے۔ ہمیں گتانک کی گنتی کرنے کی ضرورت نہیں ہے۔

یہ مثال یقیناً صرف مثال کے لیے ہے: عملی طور پر، ہائپر کیوب میں جانے کا پورا مقصد ہمیں انفرادی بٹس سے نمٹنے کی اجازت دینا ہے۔ فبونیکی نمبروں کی گنتی کرنے کا بائنیئس مقامی طریقہ یہ ہے کہ ایک اعلیٰ جہتی کیوب کا استعمال کیا جائے، جو کہ 16 بٹس کے فی گروپ میں ایک نمبر کو محفوظ کرتا ہے۔ اس کے لیے تھوڑی سی بنیاد پر عددی اضافے کو نافذ کرنے کے لیے کچھ ہوشیاری کی ضرورت ہے، لیکن بائنیئس کے لیے، یہ زیادہ مشکل نہیں ہے۔

اب، مٹانے والے کوڈز کو دیکھتے ہیں۔ STARKs کے کام کرنے کا طریقہ یہ ہے کہ آپ n اقدار لیتے ہیں، Reed-Solomon انہیں مزید قدروں تک پھیلاتے ہیں (عام طور پر 8n، عام طور پر 2n اور 32n کے درمیان)، پھر تصادفی طور پر توسیع سے مرکل کی کچھ شاخیں منتخب کریں اور ان پر کسی قسم کی جانچ کریں۔ ہائپر کیوب کی ہر جہت میں لمبائی 2 ہوتی ہے۔ لہذا، اسے براہ راست پھیلانا عملی نہیں ہے: 16 اقدار سے مرکل کی شاخوں کے نمونے لینے کے لیے کافی گنجائش نہیں ہے۔ تو ہم یہ کیسے کرتے ہیں؟ آئیے فرض کریں کہ ہائپر کیوب ایک مربع ہے!

سادہ بائنیئس – ایک مثال

دیکھیں یہاں پروٹوکول کے ازگر کے نفاذ کے لیے۔

آئیے ایک مثال دیکھتے ہیں، سہولت کے لیے اپنے فیلڈز کے بطور باقاعدہ عدد کا استعمال کرتے ہوئے (حقیقی نفاذ میں، شادی بائنری فیلڈ عناصر کا استعمال کرتے ہیں)۔ سب سے پہلے، ہم ہائپر کیوب کو انکوڈ کرتے ہیں جسے ہم مربع کے طور پر جمع کرنا چاہتے ہیں:

اب، ہم Reed-Solomon طریقہ استعمال کرتے ہوئے مربع کو بڑھاتے ہیں۔ یعنی، ہم ہر قطار کو ایک ڈگری 3 کثیر الجہتی کے طور پر دیکھتے ہیں جس کا اندازہ x = { 0, 1, 2, 3 } پر کیا جاتا ہے اور اسی کثیر الجہتی کا اندازہ x = { 4, 5, 6, 7 } پر کرتے ہیں: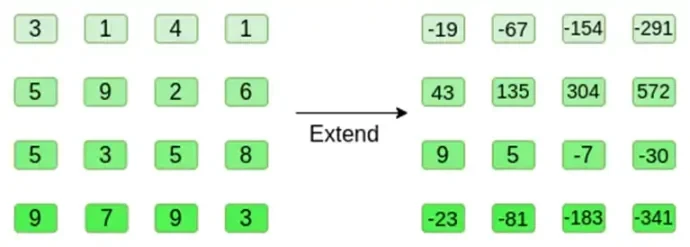

نوٹ کریں کہ تعداد واقعی بڑی ہو سکتی ہے! یہی وجہ ہے کہ عملی نفاذ میں ہم باقاعدہ انٹیجرز کے بجائے ہمیشہ محدود فیلڈز کا استعمال کرتے ہیں: اگر ہم انٹیجرز ماڈیولو 11 استعمال کرتے ہیں، مثال کے طور پر، پہلی قطار کی توسیع صرف [3, 10, 0, 6] ہوگی۔

اگر آپ ایکسٹینشن کو آزمانا چاہتے ہیں اور خود نمبروں کی تصدیق کرنا چاہتے ہیں، تو آپ یہاں میرا سادہ Reed-Solomon ایکسٹینشن کوڈ استعمال کر سکتے ہیں۔

اگلا، ہم اس ایکسٹینشن کو کالم کے طور پر دیکھتے ہیں اور کالم کا مرکل ٹری بناتے ہیں۔ مرکل کے درخت کی جڑ ہمارا عزم ہے۔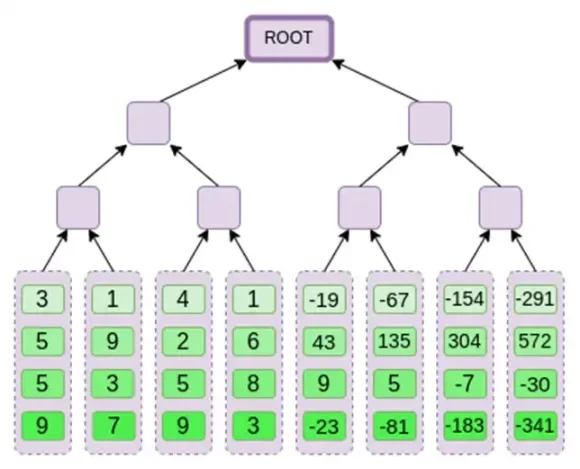

اب، فرض کرتے ہیں کہ کہنے والا کسی وقت اس کثیر الجہتی r = {r 0, r 1, r 2, r 3 } کی گنتی کو ثابت کرنا چاہتا ہے۔ Binius میں ایک لطیف فرق ہے جو اسے دیگر کثیر الجہتی کمٹمنٹ اسکیموں کے مقابلے میں کمزور بناتا ہے: کہنے والے کو مرکل روٹ سے وابستگی سے پہلے s کو نہیں جاننا چاہئے یا اس کا اندازہ لگانے کے قابل نہیں ہونا چاہئے (دوسرے الفاظ میں، r ایک چھدم بے ترتیب قدر ہونی چاہئے جس پر منحصر ہے مرکل جڑ)۔ یہ ڈیٹا بیس کی تلاش کے لیے اسکیم کو بیکار بنا دیتا ہے (مثال کے طور پر، ٹھیک ہے، آپ نے مجھے مرکل روٹ دیا، اب مجھے ثابت کریں P(0, 0, 1, 0)!)۔ لیکن زیرو نالج پروف پروٹوکول جو ہم اصل میں استعمال کرتے ہیں عام طور پر ڈیٹا بیس کی تلاش کی ضرورت نہیں ہوتی ہے۔ انہیں صرف ایک بے ترتیب تشخیصی نقطہ پر کثیر الثانی کو چیک کرنے کی ضرورت ہوتی ہے۔ لہذا یہ پابندی ہمارے مقاصد کو اچھی طرح سے پورا کرتی ہے۔

فرض کریں کہ ہم r = { 1, 2, 3, 4 } کا انتخاب کرتے ہیں (کثیریت کا اندازہ -137 ہوتا ہے؛ آپ اس کوڈ کا استعمال کرکے اس کی تصدیق کر سکتے ہیں)۔ اب ہم ثبوت کی طرف آتے ہیں۔ ہم r کو دو حصوں میں تقسیم کرتے ہیں: پہلا حصہ { 1, 2 } قطار کے اندر موجود کالموں کے لکیری امتزاج کی نمائندگی کرتا ہے، اور دوسرا حصہ { 3, 4 } قطاروں کے لکیری امتزاج کی نمائندگی کرتا ہے۔ ہم ٹینسر پروڈکٹ کا حساب لگاتے ہیں اور کالموں کے لیے:

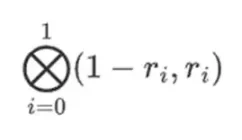
قطار کے حصے کے لیے:

اس کا مطلب ہے: ہر سیٹ میں ایک قدر کی تمام ممکنہ مصنوعات کی فہرست۔ قطار کے معاملے میں، ہمیں ملتا ہے:

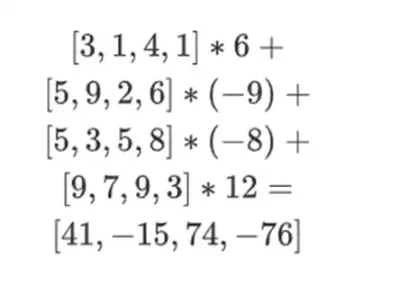
[( 1-ر 2)*( 1-ر 3)

r = { 1, 2, 3, 4 } کے ساتھ (لہذا r 2 = 3 اور r 3 = 4):

[( 1-3)*( 1-4), 3*( 1-4),( 1-3)* 4, 3* 4 ] = [ 6, -9 -8 -12 ]

اب، ہم موجودہ قطاروں کا ایک لکیری مجموعہ لے کر ایک نئی قطار ٹی کی گنتی کرتے ہیں۔ یعنی ہم لیتے ہیں:

آپ سوچ سکتے ہیں کہ یہاں کیا ہو رہا ہے ایک جزوی تشخیص کے طور پر۔ اگر ہم مکمل ٹینسر پروڈکٹ کو تمام اقدار کے مکمل ویکٹر سے ضرب دیتے ہیں، تو آپ کو حساب P(1, 2, 3, 4) = -137 ملے گا۔ یہاں، ہم نے تشخیصی نقاط کے صرف نصف کا استعمال کرتے ہوئے جزوی ٹینسر پروڈکٹ کو ضرب دیا، اور N اقدار کے گرڈ کو مربع جڑ N اقدار کی ایک قطار میں گھٹا دیا۔ اگر آپ یہ قطار کسی اور کو دیتے ہیں، تو وہ بقیہ حسابات کو تشخیصی نقاط کے دوسرے نصف کے ٹینسر پروڈکٹ کا استعمال کر کے کر سکتے ہیں۔

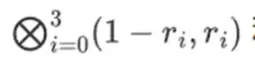
prover مندرجہ ذیل نئی قطار کے ساتھ تصدیق کنندہ فراہم کرتا ہے: t اور کچھ بے ترتیب نمونے والے کالموں کا مرکل ثبوت۔ ہماری مثالی مثال میں، ہمارے پاس prover صرف آخری کالم فراہم کرنا پڑے گا؛ حقیقی زندگی میں، پروور کو کافی سیکورٹی حاصل کرنے کے لیے درجنوں کالم فراہم کرنے کی ضرورت ہوگی۔

اب، ہم Reed-Solomon کوڈز کی لکیری کا استحصال کرتے ہیں۔ کلیدی خاصیت جس کا ہم فائدہ اٹھاتے ہیں وہ یہ ہے کہ Reed-Solomon کی توسیع کا ایک لکیری امتزاج لینے سے وہی نتیجہ ملتا ہے جو ایک لکیری امتزاج کے Reed-Solomon توسیع لینے سے ہوتا ہے۔ یہ ترتیب وار آزادی عام طور پر اس وقت ہوتی ہے جب دونوں کارروائیاں لکیری ہوں۔

تصدیق کنندہ بالکل ایسا ہی کرتا ہے۔ وہ ٹی کی گنتی کرتے ہیں، اور انہی کالموں کے لکیری مجموعوں کی گنتی کرتے ہیں جن کا پروور نے پہلے شمار کیا تھا (لیکن صرف پروور کے ذریعہ فراہم کردہ کالم)، اور تصدیق کرتے ہیں کہ دونوں طریقہ کار ایک ہی جواب دیتے ہیں۔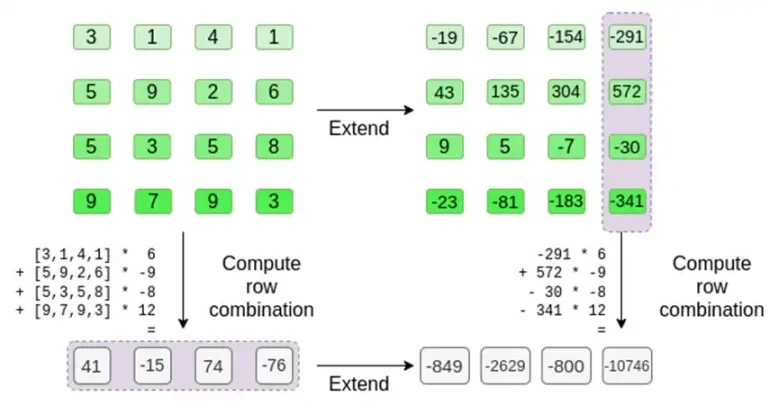

اس صورت میں، ہم t کو پھیلاتے ہیں اور ایک ہی لکیری مجموعہ ([6,-9,-8, 12]) کی گنتی کرتے ہیں، جو دونوں ایک ہی جواب دیتے ہیں: -10746۔ اس سے ثابت ہوتا ہے کہ مرکل روٹ کو نیک نیتی سے بنایا گیا تھا (یا کم از کم کافی قریب)، اور یہ کہ ٹی سے میل کھاتا ہے: کم از کم کالمز کی اکثریت ایک دوسرے کے ساتھ مطابقت رکھتی ہے۔

لیکن تصدیق کنندہ کو ایک اور چیز کی جانچ کرنے کی ضرورت ہے: کثیر الجہتی {r 0 …r 3 } کی تشخیص کی جانچ کریں۔ تصدیق کنندہ کے اب تک کے تمام اقدامات دراصل پروور کے ذریعہ دعوی کردہ قدر پر منحصر نہیں ہیں۔ یہ ہے کہ ہم اسے کیسے چیک کرتے ہیں۔ ہم "کالم حصہ" کی ٹینسر پروڈکٹ لیتے ہیں جسے ہم نے حسابی نقطہ کے طور پر نشان زد کیا ہے: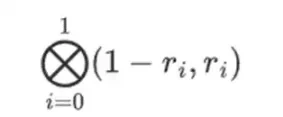

ہمارے معاملے میں، جہاں r = { 1, 2, 3, 4 } تو منتخب کالموں کا نصف حصہ { 1, 2 } ہے)، یہ اس کے برابر ہے:

اب ہم یہ لکیری مجموعہ t لیتے ہیں:

یہ براہ راست کثیرالاضلاع کو حل کرنے کے مترادف ہے۔

مندرجہ بالا سادہ Binius پروٹوکول کی مکمل وضاحت کے بہت قریب ہے۔ اس کے پہلے سے ہی کچھ دلچسپ فوائد ہیں: مثال کے طور پر، چونکہ ڈیٹا کو قطاروں اور کالموں میں الگ کیا جاتا ہے، آپ کو صرف ایک فیلڈ کی ضرورت ہوتی ہے جس کا سائز آدھا ہو۔ تاہم، یہ بائنری میں کمپیوٹنگ کے مکمل فوائد حاصل نہیں کرتا ہے۔ اس کے لیے ہمیں مکمل Binius پروٹوکول کی ضرورت ہے۔ لیکن پہلے، آئیے بائنری فیلڈز پر گہری نظر ڈالیں۔

بائنری فیلڈز

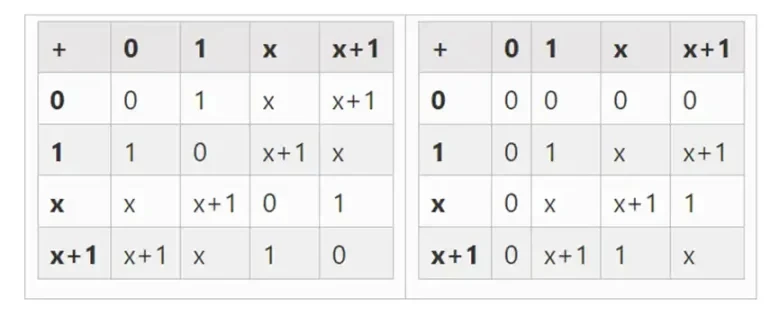
سب سے چھوٹی ممکنہ فیلڈ ریاضی کا ماڈیولو 2 ہے، جو اتنا چھوٹا ہے کہ ہم اس کے لیے اضافے اور ضرب کی میزیں لکھ سکتے ہیں:

ہم توسیع کے ذریعہ بڑے بائنری فیلڈز حاصل کرسکتے ہیں: اگر ہم F 2 (انٹیجرز ماڈیولو 2) سے شروع کریں اور پھر x کی وضاحت کریں جہاں x مربع = x + 1، ہمیں درج ذیل اضافہ اور ضرب کی میزیں ملتی ہیں:

یہ پتہ چلتا ہے کہ ہم اس تعمیر کو دہرا کر بائنری فیلڈز کو من مانی طور پر بڑے سائز تک بڑھا سکتے ہیں۔ حقیقی نمبروں پر پیچیدہ نمبروں کے برعکس، جہاں آپ ایک نیا عنصر شامل کر سکتے ہیں لیکن کبھی بھی مزید عناصر شامل نہیں کر سکتے ہیں I (quaternions موجود ہیں، لیکن وہ ریاضی کے لحاظ سے عجیب ہیں، جیسے ab ہے ba کے برابر نہیں)، محدود فیلڈز کے ساتھ آپ نئی ایکسٹینشنز شامل کر سکتے ہیں۔ ہمیشہ کے لیے خاص طور پر، ایک عنصر کی ہماری تعریف اس طرح ہے: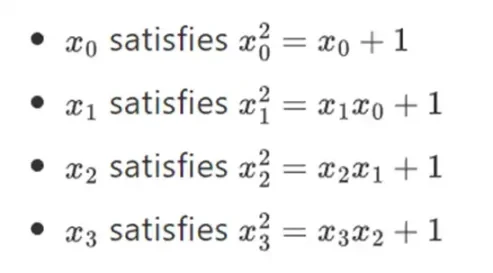

اور اسی طرح… اسے اکثر ٹاور کی تعمیر کہا جاتا ہے، کیونکہ ہر یکے بعد دیگرے توسیع کو ٹاور میں ایک نئی تہہ شامل کرنے کے بارے میں سوچا جا سکتا ہے۔ صوابدیدی سائز کے بائنری فیلڈز بنانے کا یہ واحد طریقہ نہیں ہے، لیکن اس کے کچھ منفرد فوائد ہیں جن کا بائنیئس فائدہ اٹھاتا ہے۔

ہم ان نمبروں کو بٹس کی فہرست کے طور پر پیش کر سکتے ہیں۔ مثال کے طور پر، 1100101010001111۔ پہلا بٹ 1 کے ملٹیلز کو ظاہر کرتا ہے، دوسرا بٹ x0 کے ملٹیلز کو ظاہر کرتا ہے، اور پھر درج ذیل بٹس x1 کے ملٹیلز کو ظاہر کرتا ہے: x1، x1*x0، x2، x2*x0، وغیرہ۔ یہ انکوڈنگ اچھی ہے کیونکہ آپ اسے توڑ سکتے ہیں:

یہ نسبتاً غیر معمولی اشارے ہے، لیکن میں بائنری فیلڈ عناصر کو انٹیجرز کے طور پر پیش کرنا چاہتا ہوں، جس میں دائیں جانب زیادہ موثر بٹ ہے۔ یعنی، 1 = 1، x0 = 01 = 2، 1+x0 = 11 = 3، 1+x0+x2 = 11001000 = 19، وغیرہ۔ اس نمائندگی میں، یہ 61779 ہے۔

بائنری فیلڈ میں اضافہ صرف XOR ہے (اور اسی طرح گھٹاؤ بھی ہے)؛ نوٹ کریں کہ اس کا مطلب ہے x+x = 0 کسی بھی x کے لیے۔ دو عناصر x*y کو ایک ساتھ ضرب دینے کے لیے، ایک بہت ہی آسان تکراری الگورتھم ہے: ہر نمبر کو نصف میں تقسیم کریں:

پھر، ضرب کو تقسیم کریں:

آخری حصہ صرف ایک ہے جو تھوڑا مشکل ہے، کیونکہ آپ کو آسان بنانے کے اصول لاگو کرنے ہوں گے۔ ضرب کرنے کے زیادہ موثر طریقے ہیں، جیسا کہ Karatsubas algorithm اور Fast Forier Transforms، لیکن میں اسے دلچسپی رکھنے والے قاری کے لیے ایک مشق کے طور پر چھوڑ دوں گا۔

بائنری فیلڈز میں تقسیم ضرب اور الٹ کو ملا کر کی جاتی ہے۔ سادہ لیکن سست الٹنے کا طریقہ عام فرماٹس کے چھوٹے نظریے کا اطلاق ہے۔ ایک زیادہ پیچیدہ لیکن زیادہ موثر الٹا الگورتھم بھی ہے جو آپ کو یہاں مل سکتا ہے۔ آپ بائنری فیلڈز کے اضافے، ضرب اور تقسیم کے ساتھ کھیلنے کے لیے یہاں کوڈ استعمال کر سکتے ہیں۔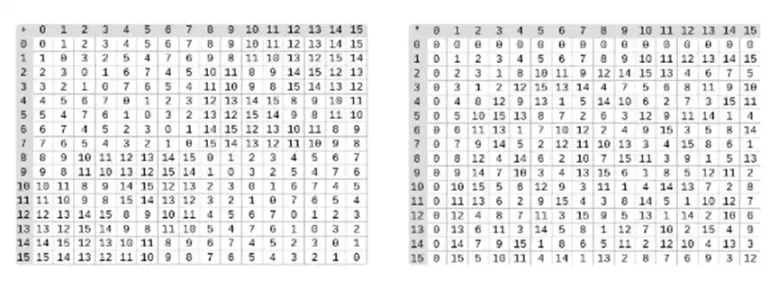

بائیں: چار بٹ بائنری فیلڈ عناصر (یعنی صرف 1، x 0، x 1، x 0x 1) کے لیے اضافی جدول۔ دائیں: چار بٹ بائنری فیلڈ عناصر کے لیے ضرب کی میز۔

اس قسم کے بائنری فیلڈ کی خوبصورتی یہ ہے کہ یہ ریگولر انٹیجرز اور ماڈیولر ریاضی کے کچھ بہترین حصوں کو یکجا کرتا ہے۔ ریگولر انٹیجرز کی طرح، بائنری فیلڈ کے عناصر بھی بے حد ہوتے ہیں: آپ جتنا چاہیں بڑھ سکتے ہیں۔ لیکن ماڈیولر ریاضی کی طرح، اگر آپ ایک مخصوص سائز کی حد کے اندر اقدار پر کام کرتے ہیں، تو آپ کے تمام نتائج ایک ہی حد میں رہیں گے۔ مثال کے طور پر، اگر آپ 42 کو لگاتار طاقتوں پر لے جاتے ہیں، تو آپ کو حاصل ہوتا ہے:

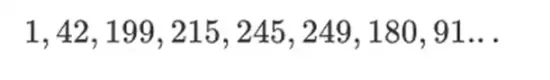
255 قدموں کے بعد، آپ 255 = 1 کی طاقت پر 42 پر واپس آ گئے ہیں، اور مثبت انٹیجرز اور ماڈیولر آپریشنز کی طرح، وہ ریاضی کے معمول کے قوانین کی پابندی کرتے ہیں: a*b=b*a، a*(b+c)= a*b+a*c، اور یہاں تک کہ کچھ عجیب نئے قوانین۔

آخر میں، بائنری فیلڈز بٹس میں ہیرا پھیری کے لیے آسان ہیں: اگر آپ 2k میں فٹ ہونے والے نمبروں کے ساتھ ریاضی کرتے ہیں، تو آپ کی تمام آؤٹ پٹ 2k بٹس میں بھی فٹ ہو جائے گی۔ اس سے بے چینی سے بچا جاتا ہے۔ Ethereums EIP-4844 میں، ایک بلاب کے انفرادی بلاکس نمبرز ہونا ضروری ہے اور اس بات کو یقینی بنانے کے لیے کہ ہر عنصر میں ذخیرہ شدہ قدر 2248 سے کم ہے، ایپلیکیشن لیئر پر اضافی چیک کریں۔ اس کا مطلب یہ بھی ہے کہ کمپیوٹرز پر بائنری فیلڈ آپریشنز بہت تیز ہیں – دونوں CPUs اور نظریاتی طور پر بہترین FPGA اور ASIC ڈیزائن۔

اس سب کا مطلب یہ ہے کہ ہم Reed-Solomon انکوڈنگ کر سکتے ہیں جیسا کہ ہم نے اوپر کیا، اس طرح سے مکمل طور پر مکمل طور پر مکمل طور پر انٹیجر دھماکے سے بچتا ہے جیسا کہ ہم نے اپنی مثال میں دیکھا، اور بہت ہی مقامی انداز میں، اس قسم کی کمپیوٹیشنز جن میں کمپیوٹر اچھے ہوتے ہیں۔ بائنری فیلڈز کی تقسیم کی خاصیت - ہم کیسے کر سکتے ہیں 1100101010001111 = 11001010 + 10001111*x 3، اور پھر اسے اپنی ضرورت کے مطابق تقسیم کریں - بہت زیادہ لچک کی اجازت دینے کے لیے بھی اہم ہے۔

مکمل Binius

دیکھیں یہاں پروٹوکول کے ازگر کے نفاذ کے لیے۔

اب ہم "مکمل بائنیئس" کی طرف بڑھ سکتے ہیں، جو "سادہ بائنیئس" کو (i) بائنری فیلڈز پر کام کرنے کے لیے ڈھالتا ہے اور (ii) ہمیں ایک بٹس کا ارتکاب کرنے دیں۔ اس پروٹوکول کو سمجھنا مشکل ہے کیونکہ یہ بٹس کے میٹرکس کو دیکھنے کے مختلف طریقوں کے درمیان آگے پیچھے ہوتا ہے۔ یقینی طور پر مجھے اس کو سمجھنے میں زیادہ وقت لگا جتنا کہ عام طور پر کرپٹوگرافک پروٹوکول کو سمجھنے میں مجھے لگتا ہے۔ لیکن ایک بار جب آپ بائنری فیلڈز کو سمجھ لیں تو اچھی خبر یہ ہے کہ بائنیئس جس "سخت ریاضی" پر انحصار کرتا ہے وہ موجود نہیں ہے۔ یہ بیضوی وکر کی جوڑی نہیں ہے، جہاں نیچے جانے کے لیے گہرے اور گہرے الجبری جیومیٹری خرگوش کے سوراخ ہوتے ہیں۔ یہاں، آپ کے پاس صرف بائنری فیلڈز ہیں۔

آئیے مکمل چارٹ کو دوبارہ دیکھتے ہیں:

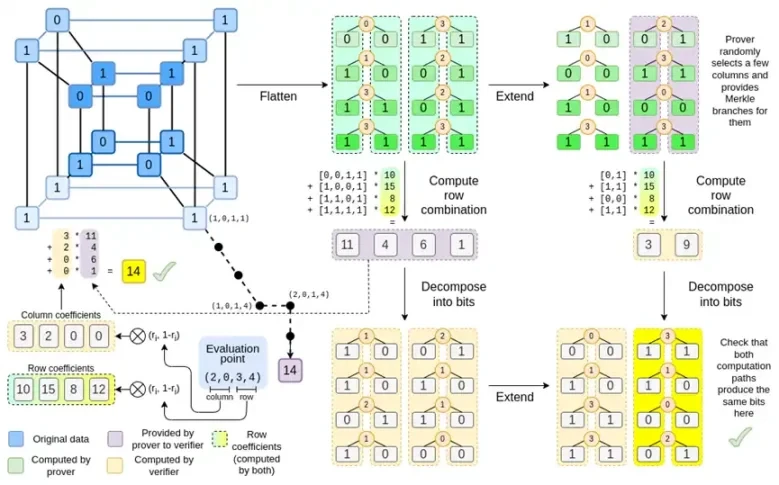
اب تک، آپ کو زیادہ تر اجزاء سے واقف ہونا چاہئے۔ ہائپر کیوب کو گرڈ میں چپٹا کرنے کا خیال، تشخیصی پوائنٹس کے ٹینسر پروڈکٹس کے طور پر قطار اور کالم کے امتزاج کو کمپیوٹنگ کرنے کا خیال، اور ریڈ-سلیمن کی توسیع کے درمیان مساوات کو جانچنے کا خیال پھر قطار کے مجموعوں کو کمپیوٹنگ کرنے اور قطار کے مجموعوں کو کمپیوٹنگ کرنے کا خیال پھر ریڈ-سلومن کی توسیع تمام سادہ Binius میں لاگو ہوتے ہیں.

مکمل Binius میں نیا کیا ہے؟ بنیادی طور پر تین چیزیں:

• ہائپر کیوب اور مربع میں انفرادی قدریں بٹس (0 یا 1) ہونی چاہئیں۔

• توسیع کا عمل بٹس کو کالموں میں گروپ کر کے اور عارضی طور پر یہ فرض کر کے کہ وہ کسی بڑے فیلڈ کے عناصر ہیں، کو مزید بٹس میں پھیلاتا ہے۔

• قطار کے امتزاج کے مرحلے کے بعد، بٹس کے قدم میں عنصر کے لحاظ سے سڑنا ہوتا ہے جو توسیع کو واپس بٹس میں بدل دیتا ہے۔

خیر دونوں صورتوں پر باری باری بحث کریں۔ سب سے پہلے، توسیع کا نیا طریقہ کار۔ Reed-Solomon کوڈز کی ایک بنیادی حد ہوتی ہے، اگر آپ n کو k*n تک بڑھانا چاہتے ہیں، تو آپ کو k*n مختلف اقدار کے ساتھ ایک فیلڈ میں کام کرنے کی ضرورت ہے جسے کوآرڈینیٹ کے طور پر استعمال کیا جا سکتا ہے۔ F 2 (عرف بٹس) کے ساتھ، آپ ایسا نہیں کر سکتے۔ تو ہم کیا کرتے ہیں، F 2 کے ملحقہ عناصر کو ایک ساتھ پیک کریں تاکہ بڑی قدریں بنائیں۔ یہاں کی مثال میں، ہم ایک وقت میں دو بٹس کو عناصر میں پیک کرتے ہیں { 0 , 1 , 2 , 3 }، جو ہمارے لیے کافی ہے کیونکہ ہماری ایکسٹینشن میں صرف چار کمپیوٹیشن پوائنٹس ہیں۔ ایک حقیقی ثبوت میں، ہم ایک وقت میں 16 بٹس واپس جا سکتے ہیں۔ اس کے بعد ہم ان پیکڈ ویلیوز پر ریڈ-سلومون کوڈ پر عمل کرتے ہیں اور انہیں دوبارہ بٹس میں پیک کرتے ہیں۔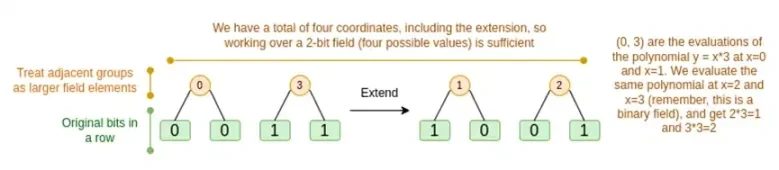

اب، قطار کے مجموعے. رینڈم پوائنٹ پر تشخیص کو خفیہ طور پر محفوظ بنانے کے لیے، ہمیں اس نقطہ کو کافی بڑی جگہ سے نمونہ کرنے کی ضرورت ہے (خود ہائپر کیوب سے بہت زیادہ)۔ لہٰذا جب کہ ہائپر کیوب کے اندر کا نقطہ تھوڑا سا ہے، ہائپر کیوب کے باہر حسابی قدر زیادہ بڑی ہوگی۔ اوپر کی مثال میں، قطار کا مجموعہ [11، 4، 6، 1] پر ختم ہوتا ہے۔

یہ ایک مسئلہ پیش کرتا ہے: ہم جانتے ہیں کہ بٹس کو ایک بڑی قدر میں کیسے گروپ کرنا ہے اور پھر اس قدر پر Reed-Solomon کی توسیع کرنا ہے، لیکن ہم قدروں کے بڑے جوڑوں کے لیے ایک ہی کام کیسے کرتے ہیں؟

Binius چال یہ ہے کہ اسے تھوڑا تھوڑا کرنا ہے: ہم ہر قدر کے ایک ایک بٹ کو دیکھتے ہیں (مثال کے طور پر، جس چیز کے لیے ہم نے 11 کا لیبل لگایا ہے، وہ [1، 1، 0، 1])، اور پھر ہم اسے قطار در قطار بڑھاتے ہیں۔ یعنی، ہم اسے ہر عنصر کی 1 قطار پر پھیلاتے ہیں، پھر x0 قطار پر، پھر x1 قطار پر، پھر x0x1 قطار پر، اور اسی طرح (ٹھیک ہے، ہمارے کھلونا مثال میں ہم وہیں رک جاتے ہیں، لیکن حقیقی عمل درآمد 128 قطاروں تک جاتا ہے (آخری ایک x6*…*x0))

جائزہ:

• ہم ہائپر کیوب میں بٹس کو گرڈ میں تبدیل کرتے ہیں۔

• اس کے بعد ہم ہر قطار کے ملحقہ بٹس کے گروپوں کو ایک بڑے فیلڈ کے عناصر کے طور پر دیکھتے ہیں اور ان پر ریاضی کے عمل کو انجام دیتے ہیں تاکہ ریڈ-سلیمون قطار کو وسیع کر سکے۔

• پھر ہم بٹس کے ہر کالم کا قطار کا مجموعہ لیتے ہیں اور ہر قطار کے لیے بٹس کا کالم آؤٹ پٹ کے طور پر حاصل کرتے ہیں (4 x 4 سے بڑے مربعوں کے لیے بہت چھوٹا)

• پھر، ہم آؤٹ پٹ کو ایک میٹرکس اور اس کے بٹس کو قطار کے طور پر سمجھتے ہیں۔

ایسا کیوں ہو رہا ہے؟ عام ریاضی میں، اگر آپ ایک عدد کو تھوڑا تھوڑا کرکے کاٹنا شروع کرتے ہیں، تو (معمول کی) کسی بھی ترتیب میں لکیری آپریشن کرنے اور وہی نتیجہ حاصل کرنے کی صلاحیت ٹوٹ جاتی ہے۔ مثال کے طور پر، اگر میں نمبر 345 سے شروع کرتا ہوں، اور میں اسے 8 سے ضرب کرتا ہوں، تو 3 سے، مجھے 8280 ملتا ہے، اور اگر میں ان دو آپریشنوں کو الٹا کرتا ہوں، تو مجھے بھی 8280 ملتا ہے۔ دو مراحل کے درمیان، یہ ٹوٹ جاتا ہے: اگر آپ 8x کرتے ہیں، تو 3x، آپ کو ملتا ہے: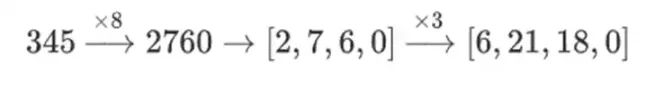

لیکن اگر آپ 3x کرتے ہیں، تو 8x، آپ کو ملتا ہے:

لیکن ٹاور ڈھانچے کے ساتھ بنائے گئے بائنری فیلڈز میں، یہ نقطہ نظر کام کرتا ہے۔ وجہ ان کی علیحدگی ہے: اگر آپ ایک بڑی قدر کو چھوٹی قدر سے ضرب دیتے ہیں، تو جو کچھ ہر طبقہ پر ہوتا ہے وہ ہر طبقہ پر رہتا ہے۔ اگر ہم 1100101010001111 کو 11 سے ضرب دیتے ہیں تو یہ 1100101010001111 کے پہلے سڑنے کے برابر ہے، جو کہ

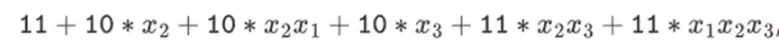
پھر ہر جزو کو 11 سے ضرب دیں۔

یہ سب ایک ساتھ ڈالنا

عام طور پر، زیرو نالج پروف سسٹم ایک کثیر نام کے بارے میں بیانات دے کر کام کرتے ہیں جو ایک ہی وقت میں بنیادی تشخیص کے بارے میں بیانات کی نمائندگی کرتے ہیں: بالکل اسی طرح جیسے ہم نے فبونیکی مثال میں دیکھا، F(X+ 2)-F(X+ 1)-F( X) = Z(X)*H(X) فبونیکی کیلکولیشن کے تمام مراحل کو چیک کرتے ہوئے۔ ہم بے ترتیب پوائنٹس پر تشخیص کو ثابت کرکے کثیر الثانی کے بارے میں بیانات کو چیک کرتے ہیں۔ بے ترتیب پوائنٹس کی یہ جانچ پوری کثیرالاضلاع کی جانچ کی نمائندگی کرتی ہے: اگر کثیر الثانی مساوات مماثل نہیں ہے، تو اس بات کا بہت کم امکان ہے کہ یہ کسی مخصوص بے ترتیب کوآرڈینیٹ سے میل کھاتا ہے۔

عملی طور پر، غیر موثریت کا ایک بڑا ذریعہ یہ ہے کہ حقیقی پروگراموں میں، ہم جن نمبروں سے نمٹتے ہیں ان میں سے زیادہ تر چھوٹے ہوتے ہیں: لوپس کے لیے اشاریے، صحیح/غلط اقدار، کاؤنٹرز، اور اس طرح کی چیزیں۔ تاہم، جب ہم مرکل پروف پر مبنی چیک کو محفوظ بنانے کے لیے درکار فالتو پن فراہم کرنے کے لیے Reed-Solomon انکوڈنگ کے ساتھ ڈیٹا کو بڑھاتے ہیں، تو زیادہ تر اضافی قدریں فیلڈ کے پورے سائز کو لے جاتی ہیں، چاہے اصل قدر چھوٹی ہو۔

اسے ٹھیک کرنے کے لیے، ہم اس فیلڈ کو ہر ممکن حد تک چھوٹا بنانا چاہتے ہیں۔ Plonky 2 ہمیں 256-bit نمبروں سے 64-bit نمبروں پر لے گیا، اور پھر Plonky 3 نے اسے مزید 31 بٹس تک گرا دیا۔ لیکن یہ بھی بہترین نہیں ہے۔ بائنری فیلڈز کے ساتھ، ہم سنگل بٹس سے نمٹ سکتے ہیں۔ یہ انکوڈنگ کو گھنا بناتا ہے: اگر آپ کے اصل بنیادی ڈیٹا میں n بٹس ہیں، تو آپ کی انکوڈنگ میں n بٹس ہوں گے، اور توسیع میں 8*n بٹس ہوں گے، بغیر کسی اضافی اوور ہیڈ کے۔

اب، اس چارٹ کو تیسری بار دیکھتے ہیں:

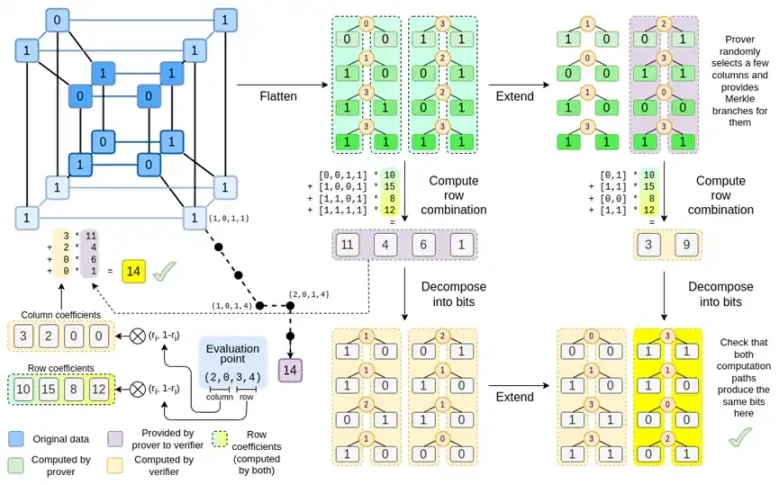
Binius میں، ہم ایک کثیر لکیری کثیر الثانی پر کام کرتے ہیں: ایک ہائپر کیوب P(x0, x1,…xk) جہاں واحد تشخیص P(0, 0, 0, 0), P(0, 0, 0, 1) تک P( 1، 1، 1، 1)، اس ڈیٹا کو تھامے رکھیں جس کا ہمیں خیال ہے۔ کسی خاص مقام پر حساب کو ثابت کرنے کے لیے، ہم اسی ڈیٹا کو مربع کے طور پر دوبارہ تشریح کرتے ہیں۔ اس کے بعد ہم ہر قطار کو بڑھاتے ہیں، Reed-Solomon انکوڈنگ کا استعمال کرتے ہوئے بے ترتیب مرکل برانچ کے سوالات کے خلاف سیکیورٹی کے لیے درکار ڈیٹا فالتو پن فراہم کرتے ہیں۔ اس کے بعد ہم قطاروں کے بے ترتیب لکیری مجموعوں کی گنتی کرتے ہیں، گتانکوں کو ڈیزائن کرتے ہیں تاکہ نئی مشترکہ قطار درحقیقت اس حسابی قدر پر مشتمل ہو جس کا ہمیں خیال ہے۔ یہ نئی بنائی گئی قطار (128 بٹ قطار کے طور پر دوبارہ تشریح کی گئی ہے) اور مرکل برانچز کے ساتھ تصادفی طور پر منتخب کردہ کچھ کالم تصدیق کنندہ کو بھیجے جاتے ہیں۔

تصدیق کنندہ پھر توسیعی قطار کا مجموعہ (یا زیادہ واضح طور پر، توسیعی کالم) اور توسیعی قطار کے امتزاج کو انجام دیتا ہے اور تصدیق کرتا ہے کہ دونوں مماثل ہیں۔ اس کے بعد یہ کالم کے امتزاج کی گنتی کرتا ہے اور چیک کرتا ہے کہ یہ پروور کے ذریعہ دعوی کردہ قدر واپس کرتا ہے۔ یہ ہمارا پروف سسٹم ہے (یا زیادہ واضح طور پر، کثیر الثانی کمٹمنٹ اسکیم، جو کہ پروف سسٹم کا ایک اہم جزو ہے)۔

ہم نے ابھی تک کیا احاطہ نہیں کیا؟

• قطاروں کو وسعت دینے کے لیے ایک موثر الگورتھم درکار ہے تاکہ درست کرنے والے کو کمپیوٹیشنل طور پر موثر بنایا جا سکے۔ ہم فاسٹ فوئیر ٹرانسفارم کو بائنری فیلڈز پر استعمال کرتے ہیں، جو یہاں بیان کیا گیا ہے (حالانکہ اس پر عمل درآمد مختلف ہوگا، کیونکہ یہ پوسٹ ایک کم موثر تعمیر کا استعمال کرتی ہے جو تکراری توسیع پر مبنی نہیں ہے)۔

• ریاضی کے لحاظ سے۔ غیر متغیر کثیر الثانیات آسان ہیں کیونکہ آپ حساب میں ملحقہ مراحل کو جوڑنے کے لیے F(X+2)-F(X+1)-F(X) = Z(X)*H(X) جیسی چیزیں کر سکتے ہیں۔ ہائپر کیوب میں، اگلے مرحلے کی وضاحت X+1 کے مقابلے میں بہت کم ہے۔ آپ X+k، k کے اختیارات کر سکتے ہیں، لیکن یہ جمپنگ رویہ Binius کے بہت سے اہم فوائد کی قربانی دیتا ہے۔ بائنیئس پیپر حل کی وضاحت کرتا ہے۔ سیکشن 4.3 دیکھیں) لیکن یہ اپنے آپ میں ایک گہرا خرگوش سوراخ ہے۔

• مخصوص ویلیو چیک کو محفوظ طریقے سے کیسے کریں۔ فبونیکی مثال کے لیے کلیدی حدود کے حالات کی جانچ پڑتال کی ضرورت ہے: F(0)=F(1)=1 اور F(100) کی قدریں۔ لیکن اصل Binius کے لیے، معلوم کیلکولیشن پوائنٹس پر چیک کرنا غیر محفوظ ہے۔ نام نہاد سم چیکنگ پروٹوکول کا استعمال کرتے ہوئے، معلوم کیلکولیشن چیکس کو نامعلوم کیلکولیشن چیک میں تبدیل کرنے کے کچھ کافی آسان طریقے ہیں۔ لیکن ہم یہاں ان کا احاطہ نہیں کریں گے۔

• لوک اپ پروٹوکول، ایک اور ٹیکنالوجی جو حال ہی میں بڑے پیمانے پر استعمال کی گئی ہے، انتہائی موثر پروف سسٹم بنانے کے لیے استعمال کی جاتی ہے۔ Binius کو کئی ایپلی کیشنز کے لیے تلاش کے پروٹوکول کے ساتھ مل کر استعمال کیا جا سکتا ہے۔

• مربع جڑ کی تصدیق کے وقت سے آگے۔ مربع جڑیں مہنگی ہیں: 2^32 بٹس کا ایک Binius ثبوت تقریباً 11 MB لمبا ہے۔ آپ Binius ثبوتوں کے ثبوت بنانے کے لیے دوسرے پروف سسٹمز کا استعمال کر کے اس کی تلافی کر سکتے ہیں، جس سے آپ کو چھوٹے پروف سائز کے ساتھ Binius پروف کی کارکردگی ملتی ہے۔ دوسرا آپشن زیادہ پیچیدہ FRI-Binius پروٹوکول ہے، جو ملٹی لوگارتھمک سائز کا ثبوت بناتا ہے (بالکل باقاعدہ FRI کی طرح)۔

• Binius کس طرح SNARK دوستی کو متاثر کرتا ہے۔ بنیادی خلاصہ یہ ہے کہ اگر آپ Binius استعمال کرتے ہیں، تو آپ کو حسابات کو ریاضی کے موافق بنانے کے بارے میں مزید پرواہ کرنے کی ضرورت نہیں ہے: باقاعدہ ہیشنگ اب روایتی ریاضی کی ہیشنگ، ضرب ماڈیولو 2 سے 32 کی طاقت یا modulo 2 کی طاقت سے زیادہ موثر نہیں ہے۔ 256 اب ضرب ماڈیولو 2 وغیرہ کی طرح تکلیف دہ نہیں ہے۔ لیکن یہ ایک پیچیدہ موضوع ہے۔ جب سب کچھ بائنری میں کیا جاتا ہے تو بہت سی چیزیں بدل جاتی ہیں۔

میں آنے والے مہینوں میں بائنری فیلڈ پر مبنی پروف ٹیکنالوجی میں مزید بہتری دیکھنے کی توقع کرتا ہوں۔

یہ مضمون انٹرنیٹ سے حاصل کیا گیا ہے: Vitalik: Binius، بائنری فیلڈز کے لیے موثر ثبوت

متعلقہ: بی این بی کوائن بحالی کے نشانات دکھاتا ہے: نیا سالانہ اعلیٰ نظر آتا ہے۔

مختصر میں BNB کی قیمت $550 سے واپس $593 مزاحمت کی خلاف ورزی کے قریب انچ تک پہنچ گئی۔ قیمت کے اشاریوں نے تیزی کی رفتار کو دوبارہ حاصل کر لیا ہے، جو 8% اضافے کو سپورٹ کرتا ہے۔ 4.03 پر تیز تناسب ممکنہ طور پر نئے سرمایہ کاروں کو ایکسچینج ٹوکن کی طرف لے جائے گا۔ مارچ BNB Coin کے لیے ایک سازگار مہینہ تھا، جس میں کرپٹو کرنسی نے تصحیح کا تجربہ کرنے سے چند دنوں کے اندر اندر سال کے لیے دو نئی بلندیاں حاصل کیں۔ بحالی کے تقریباً دو ہفتے کے عرصے کے بعد، BNB Coin 2024 میں ممکنہ طور پر ایک نئی بلندی تک پہنچنے کے آثار دکھا رہا ہے۔ لیکن کیا ایسا سنگ میل حاصل کیا جا سکتا ہے؟ BNB امید افزا لگ رہا ہے $550 سپورٹ لیول سے واپسی کے بعد، BNB Coin کی قدر اس تجزیہ کے وقت بڑھ کر $581 ہو گئی ہے۔ یہ بہتری altcoin کے رسک ریٹرن پروفائل میں بحالی کی عکاسی کرتی ہے،…