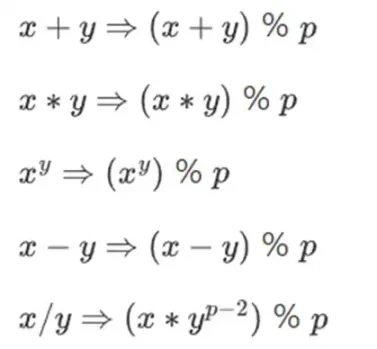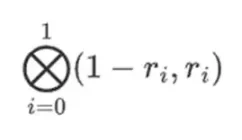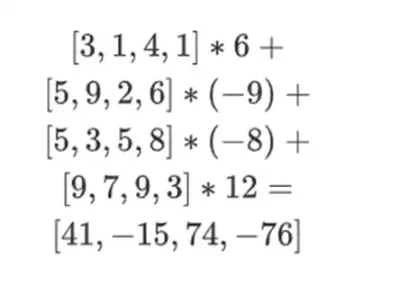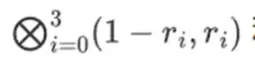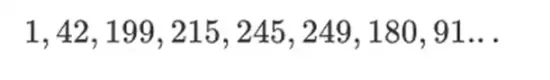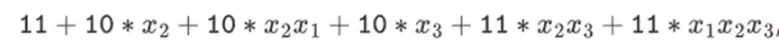Vitalik: Binius, ikili alanlar için etkili kanıtlar

Orijinal makalenin yazarı: Vitalik Buterin

Orijinal çeviri: Kate, MarsBit

Bu yazı öncelikle genel olarak 2019 dönemi kriptografisine ve özellikle SNARK'lara ve STARK'lara aşina olan okuyucular içindir. Eğer değilseniz, önce bunları okumanızı öneririm. Geri bildirimleri ve yorumları için Justin Drake, Jim Posen, Benjamin Diamond ve Radi Cojbasic'e özellikle teşekkür ederiz.

Geçtiğimiz iki yılda STARK'lar, çok karmaşık ifadelerin (örneğin bir Ethereum bloğunun geçerli olduğunu kanıtlamak) kolayca doğrulanabilir kriptografik kanıtları verimli bir şekilde oluşturmak için anahtar ve yeri doldurulamaz bir teknoloji haline geldi. Bunun temel nedenlerinden biri alan boyutunun küçük olmasıdır: Eliptik eğrilere dayanan SNARK'lar, yeterince güvenli olmak için 256 bitlik tamsayılar üzerinde çalışmanızı gerektirirken, STARK'lar çok daha küçük alan boyutlarını daha yüksek verimlilikle kullanmanıza olanak tanır: ilk olarak Goldilocks alanı (64 bit tamsayı), ardından Mersenne 31 ve BabyBear (her ikisi de 31 bit). Bu verimlilik nedeniyle gyapay zekans, Goldilocks'u kullanan Plonky 2, birçok hesaplama türünü kanıtlamada öncekilerden yüzlerce kat daha hızlıdır.

Doğal bir soru şudur: Bu eğilimi mantıksal sonucuna götürebilir ve doğrudan sıfırlar ve birler üzerinde çalışarak daha hızlı çalışan kanıt sistemleri oluşturabilir miyiz? Binius'un onu üç yıl önceki SNARK'lardan ve STARK'lardan çok farklı kılan bir takım matematiksel hileler kullanarak yapmaya çalıştığı şey tam olarak budur. Bu yazı, küçük alanların kanıt oluşturmayı neden daha verimli hale getirdiğini, ikili alanların neden benzersiz derecede güçlü olduğunu ve Binius'un ikili alanlardaki kanıtları bu kadar verimli hale getirmek için kullandığı püf noktalarını açıklamaktadır.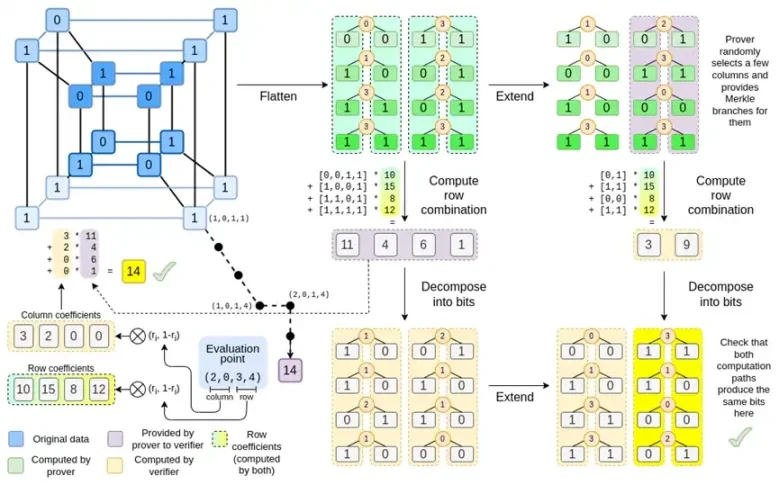

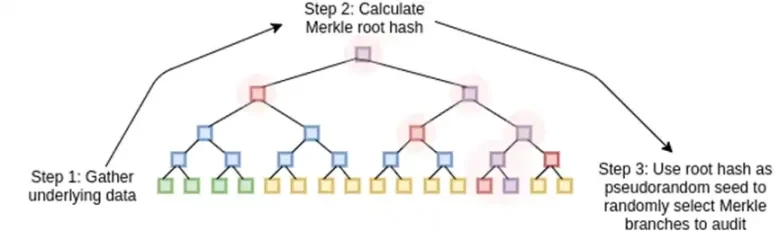
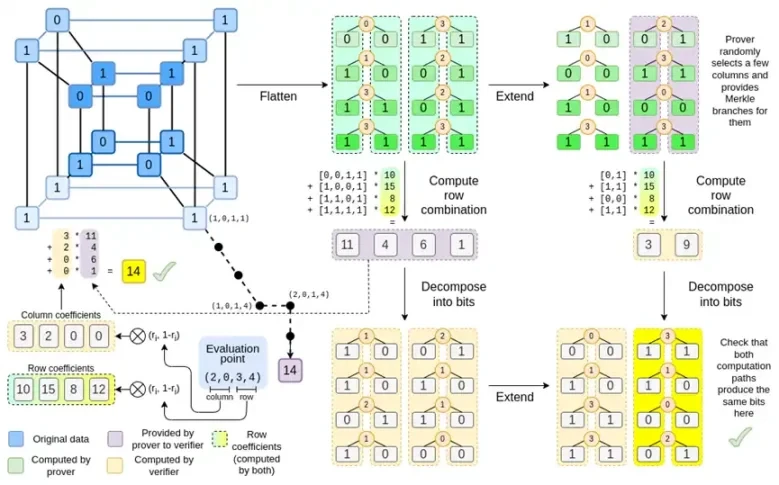
Binius, bu yazının sonunda bu diyagramın her parçasını anlayabilecek durumda olacaksın.

İnceleme: sonlu alanlar

Kriptografik kanıt sistemlerinin temel görevlerinden biri, sayıları küçük tutarken büyük miktarda veri üzerinde çalışmaktır. Büyük bir programla ilgili bir ifadeyi birkaç sayı içeren bir matematik denklemine sıkıştırabilirseniz, ancak bu sayılar orijinal program kadar büyükse, o zaman hiçbir şey kazanmamışsınız demektir.

Sayıları küçük tutarken karmaşık aritmetik yapmak için kriptograflar genellikle modüler aritmetik kullanır. Bir asal sayı modülü p seçiyoruz. % operatörü kalanın alınması anlamına gelir: 15% 7 = 1, 53% 10 = 3, vb. (Cevabın her zaman negatif olmadığını unutmayın; örneğin -1% 10 = 9)

Modüler aritmetiği zaman toplama ve çıkarma bağlamında görmüş olabilirsiniz (örneğin, saat 9'dan 4 saat sonra saat kaç?). Ancak burada sadece bir sayıyı modulo olarak ekleyip çıkarmıyoruz; ayrıca çarpabilir, bölebilir ve üslü sayılar alabiliriz.

Yeniden tanımlıyoruz:

Yukarıdaki kuralların tümü kendi içinde tutarlıdır. Örneğin p = 7 ise:

5 + 3 = 1 (çünkü 8% 7 = 1)

1-3 = 5 (çünkü -2% 7 = 5)

2* 5 = 3

3/5 = 2

Bu tür yapılar için daha genel bir terim sonlu alanlardır. Sonlu alan, aritmetiğin olağan yasalarını izleyen, ancak her değerin sabit bir boyutla temsil edilebilmesi için olası değerlerin sayısının sonlu olduğu matematiksel bir yapıdır.

Modüler aritmetik (veya asal alanlar) sonlu alanın en yaygın türüdür, ancak başka bir türü daha vardır: genişleme alanları. Bir uzantı alanı görmüş olabilirsiniz: karmaşık sayılar. Yeni bir öğe hayal edip onu i olarak etiketliyoruz ve onunla matematik yapıyoruz: (3i+2)*(2i+4)=6i*i+12i+4i+8=16i+2. Aynısını asal alanın genişletilmesiyle de yapabiliriz. Daha küçük alanlarla ilgilenmeye başladıkça, asal alanların genişletilmesi güvenlik açısından giderek daha önemli hale gelir ve ikili alanlar (Binius tarafından kullanılır) pratik faydaya sahip olmak için tamamen genişletmeye dayanır.

İnceleme: Aritmetikleştirme

SNARK'ların ve STARK'ların bilgisayar programlarını kanıtlama yöntemi aritmetikten geçer: kanıtlamak istediğiniz program hakkında bir ifade alırsınız ve bunu bir polinom içeren matematiksel bir denkleme dönüştürürsünüz. Denklemin geçerli bir çözümü, programın geçerli bir şekilde yürütülmesine karşılık gelir.

Basit bir örnek olarak 100'üncü Fibonacci sayısını hesapladığımı ve bunun ne olduğunu size kanıtlamak istediğimi varsayalım. Fibonacci dizisini kodlayan bir F polinomu oluşturuyorum: yani F(0)=F(1)=1, F(2)=2, F(3)=3, F(4)=5 ve bu şekilde 100 adım boyunca devam ediyor . Kanıtlamam gereken koşul, x={0, 1…98} aralığının tamamında F(x+2)=F(x)+F(x+1) olmasıdır. Size şu oranı vererek sizi ikna edebilirim:

burada Z(x) = (x-0) * (x-1) * …(x-98). . Eğer F ve H'nin bu denklemi sağladığını sağlayabilirsem, o zaman F'nin F(x+ 2)-F(x+ 1)-F(x) aralığını sağlaması gerekir. Ek olarak F için F(0)=F(1)=1 olduğunu doğrularsam, o zaman F(100) aslında 100'üncü Fibonacci sayısı olmalıdır.

Daha karmaşık bir şeyi kanıtlamak istiyorsanız, F(x+2) = F(x) + F(x+1) basit ilişkisini, temel olarak F(x+1)'in çıktı olduğunu söyleyen daha karmaşık bir denklemle değiştirirsiniz. F(x) durumuna sahip bir sanal makineyi başlatma ve bir hesaplama adımını çalıştırma. Daha fazla adıma yer açmak için 100 sayısını daha büyük bir sayıyla (örneğin 100000000) değiştirebilirsiniz.

Tüm SNARK'lar ve STARK'lar, bireysel değerler arasındaki çok sayıda ilişkiyi temsil etmek için polinomlar (ve bazen vektörler ve matrisler) üzerinde basit denklemler kullanma fikrine dayanmaktadır. Yukarıdaki gibi bitişik hesaplama adımları arasındaki eşitliği tüm algoritmalar kontrol etmez: örneğin, PLONK bunu yapmaz ve R1CS de bunu yapmaz. Ancak en etkili kontrollerin çoğu bunu yapar çünkü aynı kontrolü (veya aynı birkaç kontrolü) birçok kez gerçekleştirerek ek yükü en aza indirmek daha kolaydır.

Plonky 2: 256 bit SNARK'lardan ve STARK'lardan 64 bit'e… yalnızca STARK'lar

Beş yıl önce, sıfır bilgi kanıtlarının farklı türlerinin makul bir özeti aşağıdaki gibiydi. İki tür kanıt vardır: (eliptik eğri tabanlı) SNARK'lar ve (karma tabanlı) STARK'lar. Teknik olarak STARK'lar bir SNARK türüdür, ancak pratikte eliptik eğri tabanlı varyantı belirtmek için "SNARK" ve karma tabanlı yapıyı belirtmek için "STARK" kullanmak yaygındır. SNARK'lar küçüktür, dolayısıyla onları çok hızlı bir şekilde doğrulayabilir ve zincire kolayca kurabilirsiniz. STARK'lar büyüktür ancak güvenilir bir kurulum gerektirmezler ve kuantum dirençlidirler.

STARK'lar, verileri bir polinom olarak ele alarak, bu polinomun hesaplamasını hesaplayarak ve genişletilmiş verilerin Merkle kökünü bir "polinom bağlılığı" olarak kullanarak çalışır.

Buradaki tarihin önemli bir parçası, eliptik eğri tabanlı SNARK'ların ilk olarak yaygın olarak kullanılmasıdır: STARK'lar, FRI sayesinde 2018 yılına kadar yeterince verimli hale gelemedi ve o zamana kadar Zcash bir yıldan fazla süredir çalışıyordu. Eliptik eğri tabanlı SNARK'ların önemli bir sınırlaması vardır: Eliptik eğri tabanlı bir SNARK kullanmak istiyorsanız bu denklemlerdeki aritmetiğin, eliptik eğri üzerindeki nokta sayısı kadar modülo yapılması gerekir. Bu büyük bir sayıdır, genellikle 2 üssü 256'ya yakındır: örneğin, bn128 eğrisi için 21888242871839275222246405745257275088548364400416034343698204186575808495617'dir. En sevdiğiniz dilde gerçek bir program hakkında, çoğu şey kullanım alanları arasında sayaçlar, for döngülerindeki indeksler, programdaki konumlar, Doğru veya Yanlışı temsil eden tek bitler ve neredeyse her zaman yalnızca birkaç basamak uzunluğunda olan diğer şeyler bulunur.

Orijinal verileriniz küçük sayılardan oluşsa bile, kanıtlama işlemi hesaplama bölümlerini, genişletmeleri, rastgele doğrusal kombinasyonları ve ortalama olarak tam boyutunuz kadar büyük, eşit veya daha fazla sayıda nesneyle sonuçlanacak diğer veri dönüşümlerini gerektirir. alan. Bu önemli bir verimsizlik yaratır: n küçük değer üzerinde bir hesaplamayı kanıtlamak için, n çok daha büyük değerler üzerinde çok daha fazla hesaplama yapmanız gerekir. Başlangıçta STARK'lar, SNARK'ın 256 bitlik alanları kullanma alışkanlığını miras aldılar ve bu nedenle aynı verimsizlikten muzdarip oldular.

Bazı polinom değerlendirmelerinin Reed-Solomon açılımı. Orijinal değer küçük olsa bile ek değerler alanın tam boyutuna genişletilir (bu durumda 2^31 – 1)

2022'de Plonky 2 piyasaya sürüldü. Plonky 2'nin ana yeniliği, aritmetik modulo'yu daha küçük bir asal sayıyla yapmaktır: 2 üssü 64 – 2 üssü 32 + 1 = 18446744067414584321. Artık her toplama veya çarpma, her zaman aşağıdaki birkaç talimatla yapılabilir. CPU ve tüm verilerin bir araya getirilmesi eskisinden 4 kat daha hızlı. Ancak bir sorun var: Bu yöntem yalnızca STARK'larda işe yarıyor. SNARK'ları kullanmaya çalışırsanız, eliptik eğriler bu kadar küçük eliptik eğriler için güvensiz hale gelir.

Güvenliği sağlamak için Plonky 2'nin ayrıca uzantı alanları da tanıtması gerekiyor. Aritmetik denklemleri kontrol etmenin temel tekniklerinden biri rastgele nokta örneklemesidir: H(x) * Z(x)'in F(x+ 2)-F(x+ 1)-F(x)'e eşit olup olmadığını kontrol etmek istiyorsanız rastgele yapabilirsiniz. bir r koordinatı seçin, H(r), Z(r), F(r), F(r+ 1) ve F(r+ 2)'yi kanıtlamak için bir polinom kararlılığı sağlayın ve ardından H(r) * Z(r) olup olmadığını doğrulayın. ) F(r+ 2)-F(r+ 1)- F(r)'ye eşittir. Eğer bir saldırgan koordinatları önceden tahmin edebilirse, o zaman saldırgan kanıt sistemini aldatabilir; bu nedenle kanıt sisteminin rastgele olması gerekir. Ancak bu aynı zamanda koordinatların, saldırganın rastgele tahmin edemeyeceği kadar geniş bir kümeden örneklenmesi gerektiği anlamına da gelir. Modül 2 üzeri 256'ya yakınsa bu kesinlikle doğrudur. Ancak 2^64 – 2^32 + 1 modülü için henüz o noktaya gelmedik ve aşağıdaki seviyeye inersek durum kesinlikle böyle değil. 2^31 – 1. Bir saldırganın şansı yaver gidene kadar iki milyar kez kanıt uydurmaya çalışması oldukça mümkündür.

Bunu önlemek için r'yi genişletilmiş bir alandan örnekliyoruz, böylece örneğin y^3 = 5 olduğunda y'yi tanımlayabilir ve 1, y ve y^2'nin kombinasyonlarını alabilirsiniz. Bu, toplam koordinat sayısını yaklaşık 2^93'e getirir. Kanıtlayıcı tarafından hesaplanan polinomların çoğu bu genişletilmiş alana girmez; bunlar sadece modulo 2^31-1 tam sayılarıdır, dolayısıyla küçük bir alan kullanmanın tüm verimini elde edersiniz. Ancak rastgele nokta kontrolleri ve FRI hesaplamaları, ihtiyaç duydukları güvenliği elde etmek için bu daha geniş alana ulaşıyor.

Küçük asal sayılardan ikili sayılara

Bilgisayarlar, daha büyük sayıları 0'lar ve 1'lerden oluşan diziler halinde temsil ederek ve toplama ve çarpma gibi işlemleri hesaplamak için bu bitlerin üzerine devreler kurarak aritmetik yapar. Bilgisayarlar özellikle 16-, 32- ve 64-bit tamsayılar için optimize edilmiştir. Örneğin, 2^64 – 2^32 + 1 ve 2^31 – 1, yalnızca bu sınırlara uydukları için değil, aynı zamanda bu sınırlara da iyi uydukları için seçildi: çarpma modulo 2^64 – 2^32 + 1 normal bir 32 bitlik çarpma yapılarak ve bit düzeyinde kaydırılarak ve çıktının birkaç yere kopyalanmasıyla gerçekleştirilebilir; Bu makale bazı püf noktalarını güzel bir şekilde açıklıyor.

Ancak hesaplamaları doğrudan ikili olarak yapmak çok daha iyi bir yaklaşım olacaktır. Peki ya 1 + 1'in bir bitten diğerine eklenmesinden kaynaklanan aktarım konusunda endişelenmenize gerek kalmadan, toplama sadece XOR olabilseydi? Peki ya çarpma aynı şekilde daha paralel hale getirilebilseydi? Bu avantajların tümü, doğru/yanlış değerlerinin tek bir bit ile temsil edilebilmesine dayanmaktadır.

İkili hesaplama yapmanın bu avantajlarını doğrudan elde etmek, Binius'un yapmaya çalıştığı şey tam olarak budur. Binius ekibi zkSummit'teki sunumlarında verimlilik kazanımlarını gösterdi:

Yaklaşık olarak aynı boyutta olmasına rağmen, 32 bitlik ikili alanlardaki işlemler, 31 bitlik Mersenne alanlarındaki işlemlere göre 5 kat daha az hesaplama kaynağı gerektirir.

Tek değişkenli polinomlardan hiperküplere

Bu mantığa inandığımızı ve her şeyi bitlerle (0 ve 1) yapmak istediğimizi varsayalım. Bir milyar biti tek bir polinomla nasıl temsil edebiliriz?

Burada iki pratik sorunla karşı karşıyayız:

1. Bir polinomun çok sayıda değeri temsil etmesi için, polinom değerlendirilirken bu değerlerin erişilebilir olması gerekir: yukarıdaki Fibonacci örneğinde F(0), F(1) … F(100) ve daha büyük bir hesaplamada , üsler milyonlarla ifade edilecek. Kullandığımız alanların bu boyutta sayılar içermesi gerekiyor.

2. Bir Merkle ağacında taahhüt ettiğimiz herhangi bir değeri kanıtlamak (tüm STARK'lar gibi) Reed-Solomon'un bunu kodlamasını gerektirir: örneğin, değerleri n'den 8n'ye genişletmek, kötü niyetli kanıtlayıcıların hesaplama sırasında bir değer oluşturarak hile yapmasını önlemek için fazlalık kullanmak. Bu aynı zamanda yeterince geniş bir alana sahip olmayı da gerektirir: Bir milyon değerden 8 milyona çıkarmak için polinomu değerlendirmek için 8 milyon farklı noktaya ihtiyacınız vardır.

Binius'un temel fikri bu iki problemi ayrı ayrı çözmek ve bunu aynı verileri iki farklı şekilde temsil ederek yapmaktır. İlk olarak polinomların kendisi. Eliptik eğri tabanlı SNARK'lar, 2019 dönemi STARK'lar, Plonky 2 ve diğerleri gibi sistemler genellikle tek bir değişken üzerindeki polinomlarla ilgilenir: F(x). Binius ise Sparta protokolünden ilham alıyor ve çok değişkenli polinomlar kullanıyor: F(x 1, x 2,… xk). Aslında, tüm hesaplama yörüngesini, her xi'nin 0 veya 1 olduğu bir hesaplama hiperküpü üzerinde temsil ediyoruz. Örneğin, bir Fibonacci dizisini temsil etmek istiyorsak ve hala bunları temsil edecek kadar büyük bir alan kullanıyorsak, şunları yapabiliriz: ilk 16 sekanslarını şöyle hayal edin: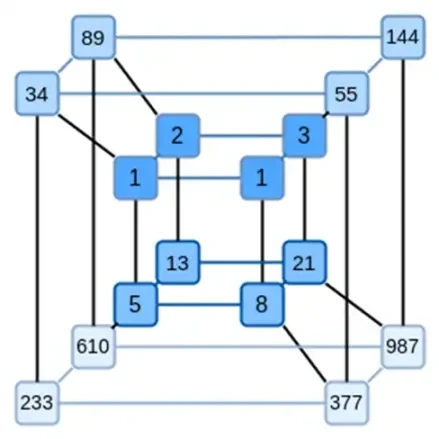

Yani, F(0,0,0,0) 1 olmalıdır, F(1,0,0,0) da 1 olmalıdır, F(0,1,0,0) 2 olmalıdır, vb. F(1,1,1,1) = 987'ye kadar. Böyle bir hiperküp hesaplama göz önüne alındığında, bu hesaplamaları üreten çok değişkenli doğrusal (her değişkende 1 derece) bir polinom vardır. Dolayısıyla bu değerler kümesinin polinomu temsil ettiğini düşünebiliriz; katsayıları hesaplamamıza gerek yok.

Bu örnek elbette sadece örnekleme amaçlıdır: Pratikte hiperkübe girmenin asıl amacı, bireysel parçalarla ilgilenmemize izin vermektir. Fibonacci sayılarını hesaplamanın Binius'a özgü yolu, örneğin 16 bitlik grup başına bir sayı depolayan daha yüksek boyutlu bir küp kullanmaktır. Bu, tamsayı toplamayı bit bazında uygulamak için biraz akıllılık gerektirir, ancak Binius için bu çok zor değil.

Şimdi silme kodlarına bakalım. STARK'ların çalışma şekli, n değer almanız, Reed-Solomon'un bunları daha fazla değere genişletmeniz (genellikle 8n, genellikle 2n ile 32n arasında), ardından genişletmeden rastgele bazı Merkle dallarını seçip bunlar üzerinde bir tür kontrol gerçekleştirmenizdir. Hiperküpün her boyutta uzunluğu 2'dir. Bu nedenle doğrudan genişletmek pratik değildir: Merkle dallarını 16 değerden örneklemek için yeterli alan yoktur. Peki bunu nasıl yapacağız? Hiperküpün bir kare olduğunu varsayalım!

Basit Binius – Bir Örnek

Görmek Burada protokolün python uygulaması için.

Kolaylık olması açısından alanlarımız olarak normal tamsayıları kullanan bir örneğe bakalım (gerçek bir uygulamada ikili alan öğelerini kullanırız). Öncelikle göndermek istediğimiz hiperküpü kare olarak kodluyoruz:

Şimdi kareyi Reed-Solomon yöntemini kullanarak genişletiyoruz. Yani, her satırı x = { 0, 1, 2, 3 }'de değerlendirilen 3. derece polinom olarak ele alırız ve aynı polinomu x = { 4, 5, 6, 7 }'de değerlendiririz: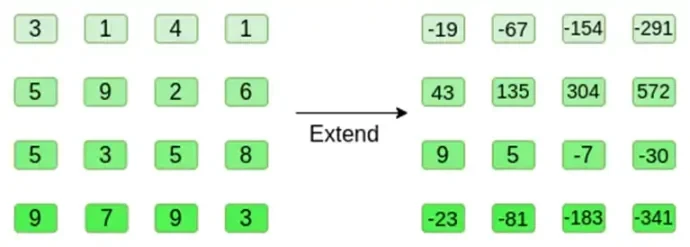

Sayıların gerçekten büyük olabileceğini unutmayın! Pratik uygulamalarda normal tamsayılar yerine her zaman sonlu alanları kullanmamızın nedeni budur: örneğin modulo 11 tamsayılarını kullanırsak, ilk satırın genişlemesi sadece [3, 10, 0, 6] olacaktır.

Uzantıyı denemek ve sayıları kendiniz doğrulamak istiyorsanız buradaki basit Reed-Solomon uzantı kodumu kullanabilirsiniz.

Daha sonra bu uzantıyı bir sütun olarak ele alıyoruz ve sütunun Merkle ağacını oluşturuyoruz. Merkle ağacının kökü bizim bağlılığımızdır.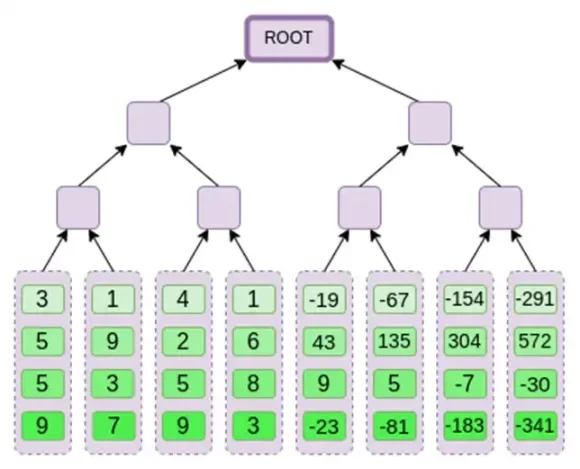

Şimdi, ispatlayıcının bir noktada bu r = {r 0, r 1, r 2, r 3 } polinomunun hesaplamasını kanıtlamak istediğini varsayalım. Binius'ta, onu diğer polinom bağlılık şemalarından daha zayıf kılan ince bir fark vardır: kanıtlayıcı, Merkle köküne bağlı kalmadan önce s'yi bilmemeli veya tahmin edememelidir (başka bir deyişle, r, aşağıdakilere bağlı olan sözde rastgele bir değer olmalıdır: Merkle kökü). Bu, şemayı veritabanı aramaları için kullanışsız hale getirir (örneğin, tamam, bana Merkle kökünü verdin, şimdi bana P(0, 0, 1, 0)'ı kanıtla!). Ancak gerçekte kullandığımız sıfır bilgi kanıt protokolleri genellikle veri tabanı aramaları gerektirmez; sadece polinomun rastgele bir değerlendirme noktasında kontrol edilmesini gerektirirler. Dolayısıyla bu kısıtlama bizim amaçlarımıza iyi hizmet ediyor.

Diyelim ki r = { 1, 2, 3, 4 } seçtiğimizi varsayalım (polinom -137 olarak değerlendirilir; bunu bu kodu kullanarak doğrulayabilirsiniz). Şimdi kanıta geçiyoruz. r'yi iki kısma ayırıyoruz: ilk kısım {1, 2 } satır içindeki sütunların doğrusal birleşimini, ikinci kısım { 3, 4 } ise satırların doğrusal birleşimini temsil ediyor. Bir tensör çarpımı hesaplıyoruz ve sütunlar için:

Satır kısmı için:

Bu şu anlama gelir: her kümedeki bir değerin tüm olası ürünlerinin listesi. Satır durumunda şunu elde ederiz:

[( 1-r 2)*( 1-r 3), ( 1-r 3), ( 1-r 2)*r 3, r 2*r 3 ]

r = { 1, 2, 3, 4 } ile (yani r 2 = 3 ve r 3 = 4):

[( 1-3)*( 1-4), 3*( 1-4),( 1-3)* 4, 3* 4 ] = [ 6, -9 -8 -12 ]

Şimdi mevcut satırların doğrusal birleşimini alarak yeni bir t satırını hesaplıyoruz. Yani şunu alıyoruz:

Burada yaşananları kısmi bir değerlendirme olarak düşünebilirsiniz. Tam tensör çarpımını tüm değerlerin tam vektörüyle çarparsak, P(1, 2, 3, 4) = -137 hesaplamasını elde edersiniz. Burada, değerlendirme koordinatlarının yalnızca yarısını kullanarak kısmi tensör çarpımını çarptık ve N değerlerinin ızgarasını tek bir karekök N değerleri satırına indirdik. Bu satırı başka birine verirseniz, hesaplamanın geri kalanını değerlendirme koordinatlarının diğer yarısının tensör çarpımını kullanarak yapabilir.

Kanıtlayıcı, doğrulayıcıya aşağıdaki yeni satırı sağlar: t ve rastgele örneklenmiş bazı sütunların Merkle kanıtı. Açıklayıcı örneğimizde, kanıtlayıcının yalnızca son sütunu sağlamasını sağlayacağız; gerçek hayatta kanıtlayıcının yeterli güvenliği sağlamak için düzinelerce sütun sağlaması gerekir.

Şimdi Reed-Solomon kodlarının doğrusallığından yararlanıyoruz. Yararlandığımız temel özellik, Reed-Solomon açılımlarının doğrusal bir kombinasyonunu almanın, doğrusal bir birleşimin Reed-Solomon açılımını almakla aynı sonucu vermesidir. Bu sıralı bağımsızlık genellikle her iki işlem de doğrusal olduğunda ortaya çıkar.

Doğrulayıcı tam olarak bunu yapar. T'yi hesaplarlar ve kanıtlayıcının daha önce hesapladığı sütunların (ancak yalnızca kanıtlayıcının sağladığı sütunların) doğrusal kombinasyonlarını hesaplarlar ve iki prosedürün aynı cevabı verdiğini doğrularlar.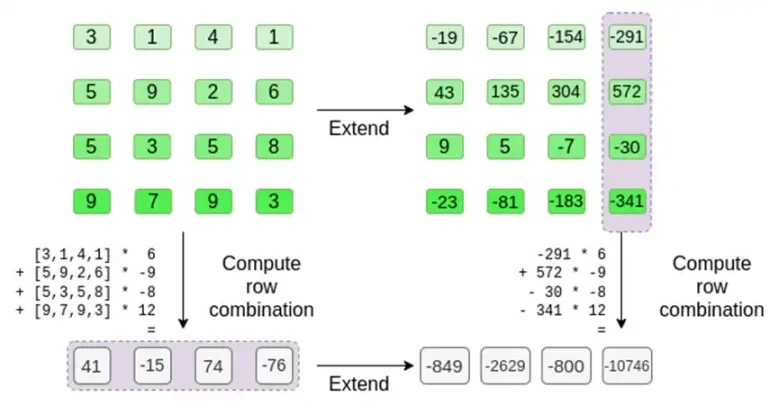

Bu durumda, t'yi genişletiriz ve her ikisi de aynı cevabı veren aynı doğrusal kombinasyonu ([6,-9,-8, 12]) hesaplarız: -10746. Bu, Merkle kökünün iyi niyetle (veya en azından yeterince yakın) inşa edildiğini ve eşleştiğini kanıtlar: en azından sütunların büyük çoğunluğu birbiriyle uyumludur.

Ancak doğrulayıcının kontrol etmesi gereken bir şey daha var: {r 0 …r 3 } polinomunun değerlendirmesini kontrol edin. Doğrulayıcının şu ana kadar attığı tüm adımlar aslında kanıtlayıcının iddia ettiği değere bağlı değildi. İşte bunu nasıl kontrol edeceğiz. Hesaplama noktası olarak işaretlediğimiz “sütun kısmı”nın tensör çarpımını alıyoruz: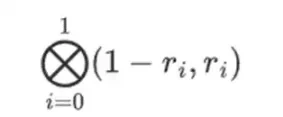

Bizim durumumuzda, r = { 1, 2, 3, 4 } yani seçilen sütunların yarısı { 1, 2 } ise), bu şuna eşdeğerdir:

Şimdi bu doğrusal kombinasyon t'yi alıyoruz:

Bu, polinomun doğrudan çözülmesiyle aynıdır.

Yukarıdakiler basit Binius protokolünün tam açıklamasına çok yakındır. Bunun zaten bazı ilginç avantajları var: örneğin, veriler satırlara ve sütunlara ayrıldığından yalnızca yarısı kadar büyüklükte bir alana ihtiyacınız var. Ancak bu, ikili hesaplamanın tüm faydalarını sağlamaz. Bunun için tam Binius protokolüne ihtiyacımız var. Ama önce ikili alanlara daha derinlemesine bir göz atalım.

İkili Alanlar

Mümkün olan en küçük alan aritmetik modulo 2'dir ve bu alan o kadar küçüktür ki onun için toplama ve çarpım tabloları yazabiliriz:

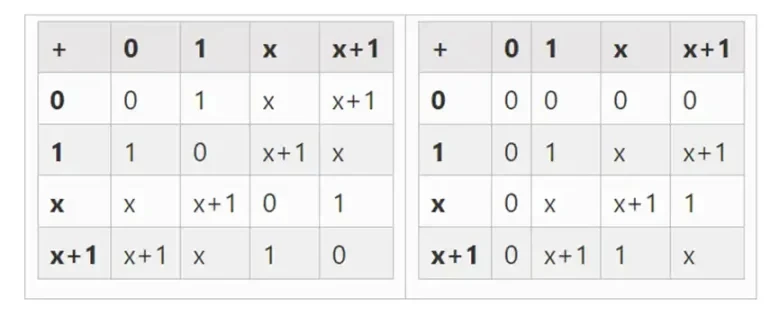
Uzatma yoluyla daha büyük ikili alanlar elde edebiliriz: F 2 (tamsayılar modulo 2) ile başlarsak ve sonra x'i (x kare = x + 1) tanımlarsak, aşağıdaki toplama ve çarpım tablolarını elde ederiz:

Bu yapıyı tekrarlayarak ikili alanları keyfi olarak büyük boyutlara genişletebileceğimiz ortaya çıktı. Yeni bir öğe ekleyebileceğiniz ancak asla daha fazla I öğesi ekleyemeyeceğiniz gerçek sayılar üzerindeki karmaşık sayılardan farklı olarak (dördeyler mevcuttur, ancak bunlar matematiksel olarak tuhaftır, örneğin ab, ba'ya eşit değildir), sonlu alanlarla yeni uzantılar ekleyebilirsiniz. sonsuza kadar. Spesifik olarak, bir elementin tanımı şu şekildedir: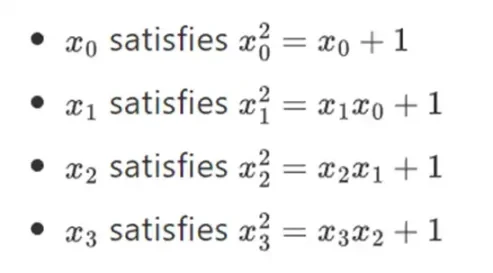

Vesaire... Buna genellikle kule inşaatı denir, çünkü birbirini takip eden her genişletme, kuleye yeni bir katman eklenmesi olarak düşünülebilir. Rasgele büyüklükte ikili alanlar oluşturmanın tek yolu bu değildir, ancak Binius'un yararlandığı bazı benzersiz avantajlara sahiptir.

Bu sayıları bit listeleri olarak temsil edebiliriz. Örneğin, 1100101010001111. İlk bit 1'in katlarını temsil eder, ikinci bit x0'ın katlarını temsil eder ve ardından takip eden bitler x1'in katlarını temsil eder: x1, x1*x0, x2, x2*x0, vb. Bu kodlama güzel çünkü onu parçalara ayırabilirsiniz:

Bu nispeten alışılmadık bir gösterimdir, ancak ikili alan öğelerini, daha verimli bit sağda olacak şekilde tam sayılar olarak temsil etmeyi seviyorum. Yani, 1 = 1, x0 = 01 = 2, 1+x0 = 11 = 3, 1+x0+x2 = 11001000 = 19 vb. Bu gösterimde bu 61779'dur.

İkili alandaki toplama sadece XOR'dur (ve bu arada çıkarma da öyle); bunun herhangi bir x için x+x = 0 anlamına geldiğini unutmayın. İki x*y öğesini birlikte çarpmak için çok basit bir yinelemeli algoritma vardır: her sayıyı ikiye bölün:

Daha sonra çarpımı bölün:

Son kısım biraz zor olan tek kısım çünkü basitleştirme kurallarını uygulamanız gerekiyor. Çarpmayı yapmanın Karatsubas algoritmasına ve Hızlı Fourier Dönüşümlerine benzer daha etkili yolları vardır, ancak bunu ilgilenen okuyucunun anlayacağı bir alıştırma olarak bırakacağım.

İkili alanlarda bölme, çarpma ve tersin birleştirilmesiyle yapılır. Basit ama yavaş ters çevirme yöntemi, genelleştirilmiş Fermats küçük teoreminin bir uygulamasıdır. Burada bulabileceğiniz daha karmaşık ama daha verimli bir ters çevirme algoritması da vardır. İkili alanların toplanması, çarpılması ve bölünmesiyle oynamak için buradaki kodu kullanabilirsiniz.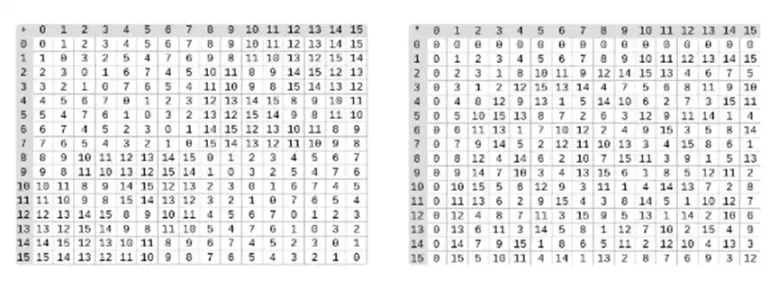

Sol: Dört bitlik ikili alan elemanları için toplama tablosu (yani yalnızca 1, x 0, x 1, x 0x 1). Sağ: Dört bitlik ikili alan elemanları için çarpım tablosu.

Bu tür ikili alanın güzelliği, düzenli tam sayıların ve modüler aritmetiğin en iyi kısımlarından bazılarını birleştirmesidir. Normal tamsayılar gibi ikili alan öğeleri de sınırsızdır: istediğiniz kadar büyüyebilirsiniz. Ancak tıpkı modüler aritmetikte olduğu gibi, belirli bir boyut sınırı dahilindeki değerler üzerinde işlem yaparsanız tüm sonuçlarınız aynı aralıkta kalacaktır. Örneğin, 42'nin ardışık kuvvetlerini alırsanız şunu elde edersiniz:

255 adımdan sonra 42 üssü 255 = 1'e geri dönersiniz ve tıpkı pozitif tamsayılar ve modüler işlemler gibi bunlar da matematiğin olağan yasalarına uyar: a*b=b*a, a*(b+c)= a*b+a*c ve hatta bazı tuhaf yeni yasalar.

Son olarak, ikili alanlar bitleri işlemek için uygundur: 2k'ye sığan sayılarla matematik yaparsanız, o zaman tüm çıktınız da 2k bit'e sığar. Bu, garipliği önler. Ethereum EIP-4844'te, bir blobun bireysel blokları modulo 52435875175126190479447740508185965837690552500527637822603658699938581184513 sayıları olmalıdır, bu nedenle ikili verileri kodlamak, uygulamada biraz alan atmayı ve ekstra kontroller yapmayı gerektirir. her öğede depolanan değerin 2248'den küçük olmasını sağlamak için katman. aynı zamanda bilgisayarlarda ikili alan işlemlerinin (hem CPU'lar hem de teorik olarak optimal FPGA ve ASIC tasarımları) süper hızlı olduğu anlamına gelir.

Bütün bunlar, Reed-Solomon kodlamasını yukarıda yaptığımız gibi, örneğimizde gördüğümüz gibi tamsayı patlamasını tamamen önleyecek şekilde ve bilgisayarların iyi olduğu hesaplama türlerini çok doğal bir şekilde yapabileceğimiz anlamına geliyor. İkili alanların bölünmüş özelliği - 1100101010001111 = 11001010 + 10001111*x 3'ü nasıl yapabiliriz ve sonra bunu ihtiyacımıza göre nasıl bölebiliriz - çok fazla esnekliğe izin vermek için de çok önemlidir.

Binius'u tamamla

Görmek Burada protokolün python uygulaması için.

Artık “basit Binius”u (i) ikili alanlar üzerinde çalışmaya ve (ii) tekli bitleri işlemeye uyarlayan “tam Binius”a geçebiliriz. Bu protokolün anlaşılması zordur çünkü bit matrislerine farklı bakış açıları arasında geçiş yapar; bunu anlamam kesinlikle kriptografik protokolleri anlamamdan daha uzun sürdü. Ancak ikili alanları anladığınızda, iyi haber şu ki Binius'un güvendiği "daha zor matematik" mevcut değil. Bu, gittikçe daha derin cebirsel geometri tavşan deliklerinin aşağı ineceği eliptik eğri eşleşmeleri değil; burada sadece ikili alanlarınız var.

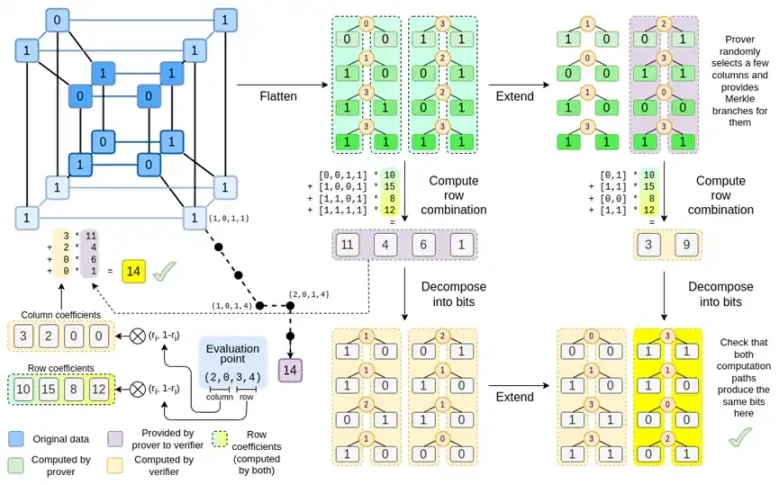
Grafiğin tamamına tekrar bakalım:

Artık bileşenlerin çoğuna aşina olmalısınız. Bir hiperküpü bir ızgaraya düzleştirme fikri, satır ve sütun kombinasyonlarını değerlendirme noktalarının tensör çarpımları olarak hesaplama fikri ve Reed-Solomon genişletmesi arasındaki denkliği kontrol etme, ardından satır kombinasyonlarını hesaplama ve satır kombinasyonlarını hesaplama ve ardından Reed-Solomon genişletmesi fikri hepsi düz Binius'ta uygulanmaktadır.

Complete Binius'taki yenilikler neler? Temel olarak üç şey:

• Hiperküp ve karedeki bireysel değerler bit (0 veya 1) olmalıdır.

• Genişletme işlemi, bitleri sütunlar halinde gruplandırarak ve geçici olarak daha büyük bir alanın öğeleri olduklarını varsayarak daha fazla bit halinde genişletir.

• Satır birleştirme adımından sonra, genişletmeyi tekrar bitlere dönüştüren öğe bazında bitlere ayrıştırma adımı vardır.

Her iki durumu da sırasıyla tartışalım. İlk olarak, yeni uzatma prosedürü. Reed-Solomon kodlarının temel bir sınırlaması vardır; eğer n'yi k*n'ye genişletmek istiyorsanız, koordinat olarak kullanılabilecek k*n farklı değere sahip bir alanda çalışmanız gerekir. F 2 (diğer adıyla bitler) ile bunu yapamazsınız. Yani yaptığımız şey, F2'nin bitişik elemanlarını daha büyük değerler oluşturacak şekilde bir araya getirmek. Buradaki örnekte, { 0 , 1 , 2 , 3 } elemanlarına aynı anda iki bit paketliyoruz, bu bizim için yeterli çünkü uzantımız yalnızca dört hesaplama noktasına sahip. Gerçek bir kanıt olarak, bir seferde 16 bit geriye gidebiliriz. Daha sonra bu paketlenmiş değerler üzerinde Reed-Solomon kodunu çalıştırıyoruz ve bunları tekrar bitlere ayırıyoruz.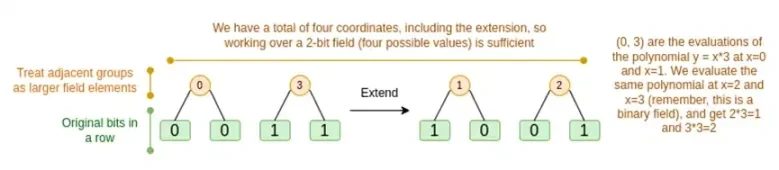

Şimdi satır kombinasyonları. Rastgele bir noktadaki değerlendirmeyi kriptografik olarak güvenli hale getirmek için, bu noktayı oldukça geniş bir alandan (hiperküpün kendisinden çok daha büyük) örneklememiz gerekir. Yani hiperküpün içindeki nokta bit iken, hiperküpün dışında hesaplanan değer çok daha büyük olacaktır. Yukarıdaki örnekte satır kombinasyonu [11, 4, 6, 1] olur.

Bu bir sorun yaratıyor: Bitleri daha büyük bir değere nasıl gruplandıracağımızı ve ardından bu değer üzerinde bir Reed-Solomon genişletmesi gerçekleştireceğimizi biliyoruz, ancak aynı şeyi daha büyük değer çiftleri için nasıl yapacağız?

Binius'un püf noktası, bunu parça parça yapmaktır: her değerin tek bir bitine bakarız (örneğin, 11 olarak etiketlediğimiz şey için, bu [1, 1, 0, 1]) ve sonra onu satır satır genişletiriz. Yani, onu her elemanın 1. satırına, sonra x0 satırına, sonra x1 satırına, sonra x0x1 satırına vb. genişletiyoruz (oyuncak örneğimizde burada duruyoruz, ancak gerçek anlamda uygulama 128 satıra kadar çıkabilir (sonuncusu x6*…*x0'dır))

gözden geçirmek:

• Hiperküpteki bitleri bir ızgaraya dönüştürüyoruz

• Daha sonra her satırdaki bitişik bit gruplarına daha büyük bir alanın elemanları olarak davranırız ve Reed-Solomon'un satırı genişletmesi için bunlar üzerinde aritmetik işlemler gerçekleştiririz.

• Daha sonra her bir bit sütununun satır kombinasyonunu alırız ve her satır için bit sütununu çıktı olarak alırız (4 x 4'ten büyük kareler için çok daha küçük).

• Daha sonra çıktıyı bir matris, bitlerini ise satırlar olarak kabul ederiz.

Bu neden oluyor? Normal matematikte, bir sayıyı parça parça dilimlemeye başlarsanız, doğrusal işlemleri herhangi bir sırayla yapma ve aynı sonucu alma (normal) yeteneği bozulur. Mesela 345 sayısıyla başlayıp önce 8 ile sonra 3 ile çarparsam 8280, bu iki işlemi tersten yaparsam yine 8280 elde ederim. iki adım arasında bozulur: 8x, ardından 3x yaparsanız şunu elde edersiniz: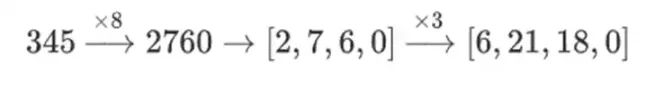

Ancak önce 3x sonra 8x yaparsanız şunu elde edersiniz:

Ancak kule yapılarıyla inşa edilen ikili alanlarda bu yaklaşım işe yarıyor. Bunun nedeni ayrılabilir olmalarıdır: Büyük bir değeri küçük bir değerle çarparsanız, her bir segmentte olup bitenler her bir segmentte kalır. 1100101010001111'i 11 ile çarparsak bu, 1100101010001111'in ilk ayrışımıyla aynı olur;

Daha sonra her bileşeni 11 ile çarpın.

Hepsini bir araya koy

Genel olarak sıfır bilgi kanıt sistemleri, aynı anda temel değerlendirmeye ilişkin ifadeleri temsil eden bir polinom hakkında ifadeler yaparak çalışır: tıpkı Fibonacci örneğinde gördüğümüz gibi, F(X+ 2)-F(X+ 1)-F( Fibonacci hesaplamasının tüm adımlarını kontrol ederken X) = Z(X)*H(X). Değerlendirmeyi rastgele noktalarda kanıtlayarak polinomla ilgili ifadeleri kontrol ediyoruz. Rastgele noktaların bu kontrolü, polinomun tamamının kontrolünü temsil eder: eğer polinom denklemi eşleşmezse, belirli bir rastgele koordinatta eşleşmesi için küçük bir şans vardır.

Pratikte verimsizliğin ana kaynaklarından biri, gerçek programlarda uğraştığımız sayıların çoğunun küçük olmasıdır: for döngülerindeki indeksler, Doğru/Yanlış değerleri, sayaçlar ve bunun gibi şeyler. Bununla birlikte, Merkle-kanıt tabanlı kontrolleri güvenli hale getirmek için gereken fazlalığı sağlamak amacıyla verileri Reed-Solomon kodlamasıyla genişlettiğimizde, orijinal değer küçük olsa bile ekstra değerlerin çoğu, alanın tüm boyutunu kaplıyor.

Bunu düzeltmek için bu alanı mümkün olduğunca küçük yapmak istiyoruz. Plonky 2 bizi 256 bitlik sayılardan 64 bitlik sayılara götürdü, ardından Plonky 3 bunu 31 bitlik sayılara düşürdü. Ancak bu bile optimal değil. İkili alanlarla tek bitlerle ilgilenebiliriz. Bu, kodlamayı yoğun hale getirir: Eğer gerçek temel verileriniz n bit içeriyorsa, kodlamanız n bit içerecek ve genişletme 8*n bit içerecek ve hiçbir ek yük olmayacaktır.

Şimdi bu grafiğe üçüncü kez bakalım:

Binius'ta çok doğrusal bir polinom üzerinde çalışıyoruz: bir hiperküp P(x0, x1,…xk) burada P(0, 0, 0, 0), P(0, 0, 0, 1)'den P('ye kadar tek değerlendirmeler 1, 1, 1, 1), önemsediğimiz verileri tutun. Belirli bir noktada bir hesaplamayı kanıtlamak için aynı verileri kare olarak yeniden yorumluyoruz. Daha sonra rastgele Merkle şube sorgularına karşı güvenlik için gerekli veri yedekliliğini sağlamak amacıyla Reed-Solomon kodlamasını kullanarak her satırı genişletiyoruz. Daha sonra satırların rastgele doğrusal kombinasyonlarını hesaplıyoruz ve katsayıları, yeni birleştirilmiş satırın aslında önemsediğimiz hesaplanan değeri içerecek şekilde tasarlıyoruz. Bu yeni oluşturulan satır (128 bitlik bir satır olarak yeniden yorumlanmıştır) ve Merkle dallarına sahip rastgele seçilen bazı sütunlar doğrulayıcıya iletilir.

Doğrulayıcı daha sonra genişletilmiş satır kombinasyonunu (veya daha doğrusu genişletilmiş sütunları) ve genişletilmiş satır kombinasyonunu gerçekleştirir ve ikisinin eşleştiğini doğrular. Daha sonra bir sütun kombinasyonunu hesaplar ve kanıtlayıcı tarafından talep edilen değeri döndürüp döndürmediğini kontrol eder. Bu bizim kanıt sistemimizdir (veya daha doğrusu, kanıt sisteminin önemli bir bileşeni olan polinom taahhüt şeması).

Henüz neyi ele almadık?

• Doğrulayıcıyı gerçekten hesaplama açısından verimli kılmak için satırları genişletecek etkili bir algoritma gereklidir. Burada açıklanan ikili alanlar üzerinde Hızlı Fourier Dönüşümü'nü kullanıyoruz (her ne kadar bu yazı özyinelemeli genişlemeye dayalı olmayan daha az verimli bir yapı kullandığından tam uygulama farklı olsa da).

• Aritmetik olarak. Tek değişkenli polinomlar kullanışlıdır çünkü hesaplamadaki bitişik adımları birbirine bağlamak için F(X+2)-F(X+1)-F(X) = Z(X)*H(X) gibi şeyler yapabilirsiniz. Hiperküpte bir sonraki adım X+1'e göre çok daha az iyi açıklanmıştır. X+k, k'nin kuvvetleri yapabilirsiniz, ancak bu atlama davranışı Binius'un birçok önemli avantajını feda eder. Binius makalesi çözümü açıklıyor. Bölüm 4.3'e bakın), ancak bu başlı başına derin bir tavşan deliğidir.

• Belirli değer kontrolleri güvenli bir şekilde nasıl yapılır? Fibonacci örneği temel sınır koşullarının kontrol edilmesini gerektiriyordu: F(0)=F(1)=1 ve F(100) değerleri. Ancak orijinal Binius için bilinen hesaplama noktalarında kontrol yapılması güvenli değildir. Bilinen hesaplama kontrollerini bilinmeyen hesaplama kontrollerine dönüştürmenin, toplam kontrol protokolleri adı verilen protokolleri kullanarak oldukça basit bazı yolları vardır; ama bunları burada ele almayacağız.

• Son dönemde yaygın olarak kullanılan bir diğer teknoloji olan arama protokolleri ise süper verimli kanıt sistemleri oluşturmak için kullanılıyor. Binius birçok uygulama için arama protokolleriyle birlikte kullanılabilir.

• Karekök doğrulama süresinin ötesinde. Karekökler pahalıdır: 2^32 bitlik bir Binius kanıtı yaklaşık 11 MB uzunluğundadır. Bunu, Binius provalarının provalarını yapmak için diğer prova sistemlerini kullanarak telafi edebilirsiniz, bu da size daha küçük prova boyutuna sahip bir Binius provasının verimliliğini sağlar. Diğer bir seçenek ise çoklu logaritmik boyutun kanıtını oluşturan (tıpkı normal FRI gibi) daha karmaşık FRI-Binius protokolüdür.

• Binius, SNARK dostu olmayı nasıl etkiler? Temel özet şu ki, Binius kullanırsanız, artık hesaplamaları aritmetik dostu hale getirmeyi umursamanıza gerek kalmaz: düzenli karma işlemi artık geleneksel aritmetik karma işleminden, modulo 2 üzeri 32'den veya modulo 2 üzeri 32'den daha verimli değildir. 256 artık çarpma modulo 2 vb. kadar acı verici değil. Ancak bu karmaşık bir konudur. Her şey ikili olarak yapıldığında birçok şey değişir.

Önümüzdeki aylarda ikili alan tabanlı kanıt teknolojisinde daha fazla gelişme görmeyi bekliyorum.

Bu makale internetten alınmıştır: Vitalik: Binius, ikili alanlar için etkili kanıtlar

İlgili: BNB Coin İyileşme İşaretleri Gösteriyor: Yeni Yılın Zirvesi Görünürde

Kısaca BNB fiyatı $550'den toparlanarak $593 direncini aşmaya yaklaştı. Fiyat göstergeleri yükseliş momentumunu yeniden kazandı ve bu da 8% yükselişini destekliyor. 4,03'teki Sharpe Oranı muhtemelen yeni yatırımcıları borsa tokenına yönlendirecek. Mart, BNB Coin için olumlu bir aydı; kripto para birimi, bir düzeltme yaşamadan sadece birkaç gün içinde yılın iki yeni zirvesine ulaştı. Yaklaşık iki haftalık bir toparlanma sürecinin ardından BNB Coin, 2024'te potansiyel olarak yeni bir zirveye ulaşacağına dair işaretler gösteriyor. Peki böyle bir dönüm noktasına ulaşılabilir mi? BNB Umut Verici Görünüyor $550 destek seviyesinden toparlanmanın ardından BNB Coin'in değeri, bu analiz sırasında $581'e yükseldi. Bu iyileşme, altcoin'in risk-getiri profilindeki iyileşmeyi yansıtıyor.