Bitcoin ve Layer2 varlık çapraz zincir teknolojisinin analizi

Orijinal başlık: Adaptör İmzaları ve Zincirler Arası Atomik Takaslara Uygulanması

Orijinal bağlantı: https://blog.bitlayer.org/Adaptor_Signatures_and_Its_Application_to_Cross-Chain_Atomic_Swaps/

Orijinal yazar: mutourend, lynndell

1 Giriş

Bitcoin'in 2. Katman ölçekleme çözümünün hızla gelişmesiyle, Bitcoin ile 2. Katman muadili arasındaki zincirler arası varlık transferlerinin sıklığı önemli ölçüde arttı. Bu eğilim, Bitlayer gibi 2. Katman teknolojilerinin sağladığı daha yüksek ölçeklenebilirlik, daha düşük işlem ücretleri ve yüksek verimlilik tarafından yönlendiriliyor. Bu ilerlemeler daha verimli ve ekonomik işlemleri kolaylaştırarak Bitcoin'in çeşitli uygulamalarda daha geniş bir şekilde benimsenmesini ve entegre edilmesini teşvik ediyor. Sonuç olarak, Bitcoin ile 2. Katman ağları arasındaki birlikte çalışabilirlik, kripto para ekosisteminin önemli bir bileşeni haline geliyor, inovasyonu teşvik ediyor ve kullanıcılara daha çeşitli ve güçlü finansal araçlar sağlıyor.

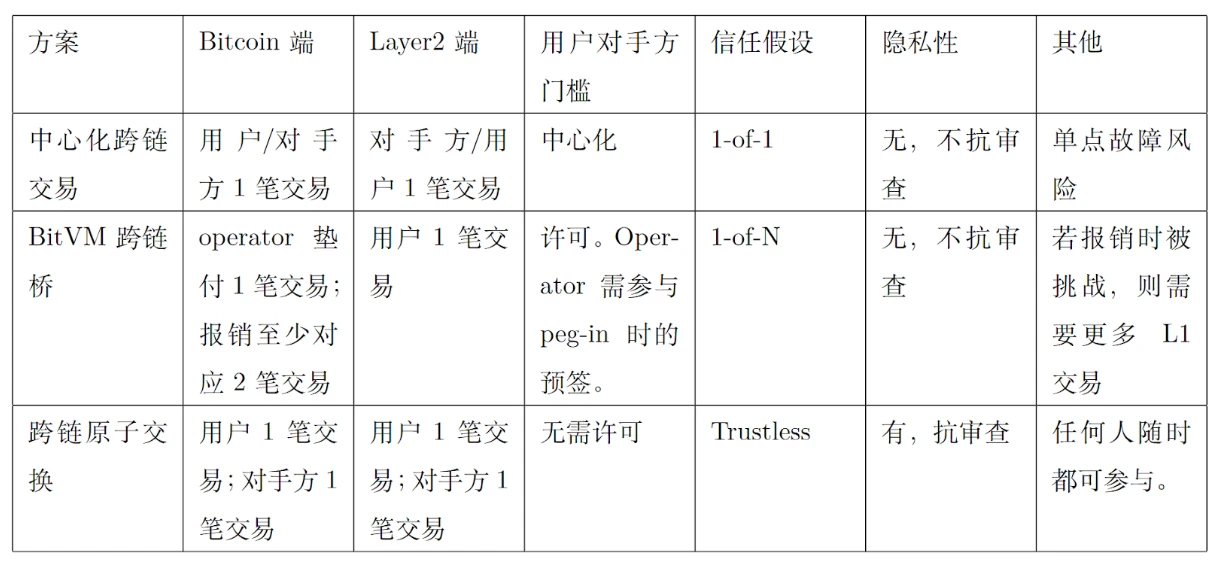
Tablo 1'de gösterildiği gibi, Bitcoin ve Katman 2 arasındaki çapraz zincir işlemleri için üç tipik çözüm vardır: merkezi çapraz zincir işlemleri, BitVM çapraz zincir köprüsü ve çapraz zincir atomik takasları. Bu üç teknoloji, güven varsayımları, güvenlik, kolaylık, işlem miktarları vb. açısından farklılık gösterir ve farklı uygulama gereksinimlerini karşılayabilir.

Tablo 1. Zincirler arası işlem teknolojilerinin karşılaştırılması

Merkezileştirilmiş zincirler arası işlemler: Kullanıcılar önce Bitcoin'i merkezi bir kuruma (örneğin bir proje partisi veya borsası) öder ve merkezi kurum eşdeğer varlıkları 2. Katman ağında kullanıcı tarafından belirtilen adrese öder, böylece zincirler arası varlık transferi tamamlanır. Bu teknolojinin avantajı hızlı olması ve eşleştirme sürecinin nispeten kolay olmasıdır çünkü merkezi kurum işlemi hızla onaylayabilir ve işleyebilir. Ancak, bu yöntemin güvenliği tamamen merkezi kurumun güvenilirliğine ve itibarına bağlıdır. Merkezi kurum teknik arızalarla, kötü niyetli saldırılarla veya temerrütlerle karşılaşırsa, kullanıcıların fonları yüksek risk altındadır. Ayrıca, merkezi zincirler arası işlemler kullanıcı gizliliğini de sızdırabilir ve kullanıcılar bu yöntemi seçerken dikkatli olmalıdır. Bu nedenle, kolaylığı ve verimliliği kullanıcılara büyük kolaylık sağlasa da, güvenlik ve güven, merkezi zincirler arası işlemlerin karşılaştığı temel zorluklardır.

BitVM çapraz zincir köprüsü: Bu teknoloji nispeten karmaşıktır. İlk olarak, Peg-in aşamasında, kullanıcılar Bitcoin'i kilitlemek için BitVM Alliance tarafından kontrol edilen çoklu imza adresine Bitcoin öderler. Karşılık gelen sayıda token Katman 2'de basılır ve token Katman 2 işlemlerini ve uygulamalarını uygulamak için kullanılır. Kullanıcı Katman 2 tokenini imha ettiğinde, Operatör ödemeyi ilerletir. Daha sonra, Operatör BitVM Alliance tarafından kontrol edilen çoklu imza havuzuna karşılık gelen sayıda Bitcoin'i geri öder. Operatörün kötü şeyler yapmasını önlemek için, geri ödeme süreci iyimser bir meydan okuma mekanizması benimser, yani herhangi bir üçüncü taraf kötü niyetli geri ödeme davranışına itiraz edebilir ve kötü davranışı engelleyebilir. Bu teknoloji iyimser bir meydan okuma mekanizması sunar, bu nedenle teknoloji nispeten karmaşıktır. Ek olarak, iyimser meydan okuma mekanizması çok sayıda meydan okuma ve yanıt işlemi içerir ve işlem ücreti yüksektir. Dolayısıyla BitVM zincirler arası köprüsü, U ihracına benzer şekilde yalnızca ultra büyük işlemler için uygundur ve dolayısıyla düşük bir kullanım sıklığına sahiptir.

Zincirler arası atomik takas: Atomik takas, merkezi olmayan kripto para birimi işlemlerini mümkün kılan bir sözleşmedir. Bu bağlamda, atomik, bir varlığın mülkiyetindeki değişikliğin aslında başka bir varlığın mülkiyetindeki değişiklik anlamına geldiği anlamına gelir. Kavram ilk olarak 2013 yılında Bitcointalk forumunda TierNolan tarafından önerildi. 4 yıl boyunca, atomik takaslar teorik alanda kaldı. Decred ve Litecoin, atomik takasları başarıyla tamamlayan ilk blok zinciri sistemleri olana kadar 2017'ye kadar değildi. Bir atomik takas iki tarafı içermelidir ve hiçbir üçüncü taraf değişim sürecini kesintiye uğratamaz veya müdahale edemez. Bu, teknolojinin merkezi olmayan, sansürsüz, iyi gizlilik korumasına sahip olduğu ve merkezi olmayan borsalarda yaygın olarak kullanılan yüksek frekanslı zincirler arası işlemleri gerçekleştirebileceği anlamına gelir. Şu anda, zincirler arası atomik takaslar 4 işlem gerektirir ve bazı planlar işlem sayısını 2'ye sıkıştırmaya çalışın, ancak bu, değişimin her iki tarafı için gerçek zamanlı çevrimiçi gereksinimleri artıracaktır. Son olarak, zincirler arası atomik takas teknolojisi esas olarak karma zaman kilitlerini ve adaptör imzalarını içerir.

Karma zaman kilitlerine (HTLC) dayalı zincirler arası atomik takaslar: Zincirler arası atomik takasları başarıyla uygulayan ilk proje, TierNolan tarafından önerilen atomik takası zincir üstü betikler (veya akıllı sözleşmeler) yardımıyla uygulamak için karma kilitler ve zaman kilitleri kullanan Decred'dir. HTLC, iki kullanıcının zamanla sınırlı kripto para birimi işlemleri yapmasına olanak tanır, yani alıcının sözleşmeye belirli bir süre içinde (blok sayısı veya blok yüksekliği tarafından belirlenir) kriptografik bir kanıt (sır) sunması gerekir, aksi takdirde fonlar göndericiye iade edilir. Alıcı ödemeyi onaylarsa, işlem başarılı olur. Bu nedenle, katılan her iki blok zincirinin de karma kilit ve zaman kilidi işlevlerine sahip olması gerekir.

HTLC atomik takasları merkezi olmayan değişim teknolojisi alanında büyük bir atılım olsa da, şu sorunlar vardır. Bu atomik takas işlemleri ve bunlarla ilişkili veriler, zincir üzerinde yürütülür ve bu da kullanıcı gizliliğinin sızmasına neden olur. Başka bir deyişle, her takas gerçekleştiğinde, aynı karma değeri her iki blok zincirinde de yalnızca birkaç blok arayla görünür. Bu, bir gözlemcinin takasa dahil olan para birimlerini, birbirine yakın bloklarda (Zaman Damgası açısından) aynı karma değerini bularak birbirine bağlayabileceği anlamına gelir. Zincirler arasında para birimlerini izlerken, kaynağı belirlemek kolaydır. Bu analiz herhangi bir ilgili kimlik verisini ortaya çıkarmasa da, üçüncü taraflar dahil olan katılımcıların kimliklerini kolayca çıkarabilir.

Adaptör imzalarına dayalı zincirler arası atomik takaslar: BasicSwap tarafından sunulan ikinci takas türü, Monero geliştiricisi Joël Gugger'ın 2020 tarihli bir makalesine dayanan adaptör imzalı atomik takas olarak adlandırılır. Bitcoin–Monero Zincirler Arası Atomik Takas Makalenin Lloyd Fourniers 2019 makalesinin bir uygulaması olduğu söylenebilir Tek Seferlik Doğrulanabilir Şifrelenmiş İmzalar, Diğer Adaptör İmzaları Bağdaştırıcı imzası, gizli verileri açığa çıkarmak için ilk imzayla birleştirilen ek bir imzadır ve iki tarafın aynı anda birbirlerine iki veri parçasını açığa çıkarmasına olanak tanır ve Monero atomik takas çiftlerini mümkün kılan komut dosyası gerektirmeyen protokolün temel bir bileşenidir.

HTLC atomik takaslarıyla karşılaştırıldığında, adaptör-imza tabanlı atomik takasların üç avantajı vardır: Birincisi, adaptör-imza takas şeması, zaman kilitleri ve karma kilitleri dahil olmak üzere gizli karma takasının dayandığı zincir üstü betikleri değiştirir. Başka bir deyişle, HTLC takasındaki gizli ve gizli karma, adaptör-imza takasında doğrudan bir ilişkiye sahip değildir. Bu nedenle, Bitcoin araştırma topluluğunda betiksiz betikler olarak adlandırılır. Ayrıca, bu tür betikler dahil olmadığından, zincirde işgal edilen alan azalır ve adaptör-imza tabanlı atomik takaslar daha hafif ve daha ucuz hale gelir. Son olarak, HTLC her zincirin aynı karma değerini kullanmasını gerektirirken, adaptör-imza atomik takasında yer alan işlemler gizlilik koruması elde etmek için birbirine bağlanamaz.

Bu makale öncelikle Schnorr/ECDSA adaptör imzasını ve zincirler arası atomik takas ilkesini tanıtmaktadır. Ardından, adaptör imzasındaki rastgele sayı güvenlik sorunlarını ve zincirler arası senaryodaki sistem heterojenliği ve algoritma heterojenliği sorunlarını analiz eder ve çözümler sunar. Son olarak, adaptör imzası genişletilir ve etkileşimsiz dijital varlık saklamayı gerçekleştirmek için uygulanır.

2. Adaptör İmzaları ve Zincirler Arası Atomik Takaslar

2.1 Schnorr Adaptör İmzaları ve Atomik Takaslar

2.2 ECDSA Adaptör İmzası ve Atomik Takas

2.2.1 Sıfır bilgi kanıtı zk{v | Ṽ = v ᐧ G, V = v ᐧ Y}

3. Güvenlik sorunları ve çözümleri

3.1 Rastgele Sayı Problemleri ve Çözümleri

3.1.1 Rastgele sayı sızıntısı sorunu

Schnorr/ECDSA bağdaştırıcı imzasının ön imzası, $r$Ȓ = r ᐧ G rastgele sayısına bağlıdır. Ek olarak, sıfır bilgi kanıtı $v$ rastgele sayısına $Ṽ=v ᐧ G, V=v ᐧ Y$ olarak bağlıdır. Rastgele sayı sızdırılırsa, özel anahtar sızdırılacaktır.

Özellikle Schnorr protokolünde, $r$ rastgele sayısı sızdırılırsa, denkleme göre kurtarılabilir.

$ŝ = r + c x.$

Özel anahtarı $x$ olarak hesaplayın.

Benzer şekilde, ECDSA protokolünde, $r$ rastgele sayısı sızdırılırsa, denkleme göre elde edilebilir.

$ŝ = r^{-1 }(karma(m)+R_x x).$

Özel anahtarı $x$ olarak hesaplayın.

Son olarak, sıfır bilgi kanıtı protokolünde, $v$ rastgele sayısı sızdırılırsa, denkleme göre elde edilebilir.

$z := v + c r.$

Rastgele sayı $r$'yi hesaplayın ve ardından rastgele sayı $r$'ye dayalı özel anahtar $x$'yi hesaplayın. Bu nedenle, rastgele sayı kullanımdan hemen sonra silinmelidir.

3.1.2 Rastgele sayı yeniden kullanım problemi

Herhangi iki çapraz zincir işlemi için, adaptör imza protokolü aynı rastgele sayıyı kullanıyorsa, bu özel anahtar sızıntısına yol açacaktır. Özellikle, Schnorr protokolünde, aynı rastgele sayı $r$ kullanılırsa, aşağıdaki denklem sisteminde yalnızca $r$ ve $x$ bilinmemektedir:

$ŝ_ 1 =r + c_ 1 x, $

$ ŝ_ 2 = r + c_ 2 x. $

Dolayısıyla denklem sistemi çözülerek $x$ özel anahtarı elde edilebilir.

Benzer şekilde, ECDSA bağdaştırıcı imza protokolünde, aynı rastgele sayı $r$ kullanılırsa, aşağıdaki denklem sisteminde yalnızca $r$ ve $x$ bilinmemektedir:

$ ŝ_ 1 = r^{-1 }(karma(m_ 1)+R_x x),$

$ ŝ_ 2 = r^{-1 }(karma(m_ 2)+R_x x).$

Dolayısıyla denklem sistemi çözülerek $x$ özel anahtarı elde edilebilir.

Son olarak, sıfır bilgi ispat protokolünde, aynı rasgele sayı $v$ kullanılırsa, aşağıdaki denklem sisteminde yalnızca $v$ ve $r$ bilinmiyor:

$z_ 1 = v+c_ 1 r, $

$ z_ 2 = v+c_ 2 r. $

Dolayısıyla denklem sistemi çözülerek $r$ rastgele sayısı elde edilebilir ve daha sonra denklem sistemi çözülerek $x$ özel anahtarı elde edilebilir.

Benzer şekilde, farklı kullanıcılar aynı rastgele sayıyı kullanırsa, özel anahtar da sızdırılır. Başka bir deyişle, aynı rastgele sayıyı kullanan iki kullanıcı denklemleri çözebilir ve birbirlerinin özel anahtarını elde edebilir. Bu nedenle, rastgele sayı yeniden kullanım sorununu çözmek için RFC 6979 kullanılmalıdır.

3.1.3 Çözüm: RFC 6979

RFC 6979, DSA ve ECDSA kullanarak deterministik dijital imzalar üretmek için bir yöntem belirtir ve bu yöntem, rastgele bir değer k üretmeyle ilişkili güvenlik sorunlarını ele alır. Geleneksel DSA ve ECDSA imzaları, her imzalama işlemi için rasgele üretilen bir rasgele sayı k'ya dayanır. Bu rasgele sayı yeniden kullanılırsa veya uygunsuz şekilde üretilirse, özel anahtarın güvenliği tehlikeye girer. RFC 6979, özel anahtardan ve imzalanacak mesajdan $k$'yi deterministik olarak türeterek rastgele bir sayı üretme ihtiyacını ortadan kaldırır. Bu, aynı özel anahtar aynı mesajı imzalamak için kullanıldığında imzanın her zaman aynı olmasını sağlar ve böylece yeniden üretilebilirlik ve öngörülebilirlik artar. Özellikle, deterministik $k$, HMAC tarafından üretilir. İşlem, özel anahtar, mesaj ve bir sayaç üzerinde bir karma değeri hesaplayan bir karma işlevi (örneğin SHA 256) içerir.

$k = SHA 256(sk, msg, sayaç).$

Yukarıdaki denklemde, basitlik adına, yalnızca özel anahtar sk, mesaj msg ve sayaç sayacı karıştırılmıştır. RFC 6979'daki gerçek hesaplama süreci daha fazla karıştırma hesaplaması içerir. Bu denklem, k'nin her mesaj için benzersiz olmasını sağlarken aynı girdi için yeniden üretilebilir olmasını ve zayıf veya tehlikeye atılmış rastgele sayı üreteçleriyle ilişkili özel anahtar ifşa riskini azaltır. Bu nedenle, RFC 6979, DSA ve ECDSA kullanarak kesin dijital imzalar için güçlü bir çerçeve sağlar, rastgele sayı üretimiyle ilgili önemli güvenlik sorunlarını çözer ve dijital imzaların güvenilirliğini ve öngörülebilirliğini artırır. Bu, onu yüksek güvenlik gerektiren ve sıkı operasyonel gereksinimleri karşılayan uygulamalar için değerli bir standart haline getirir. Schnorr/ECDSA imzalarında, RFC 6979 kullanılarak önlenmesi gereken rastgele sayı kusurları vardır. Bu nedenle, Schnorr/ECDSA tabanlı bağdaştırıcı imzalarında da bu sorunlar vardır ve bu sorunları çözmek için RFC 6979 spesifikasyonuna da ihtiyaç vardır.

3.2 Zincirler arası senaryo sorunları ve çözümleri

3.2.1 UTXO ve Hesap Modeli Sistem Heterojenliği Sorunları ve Çözümleri

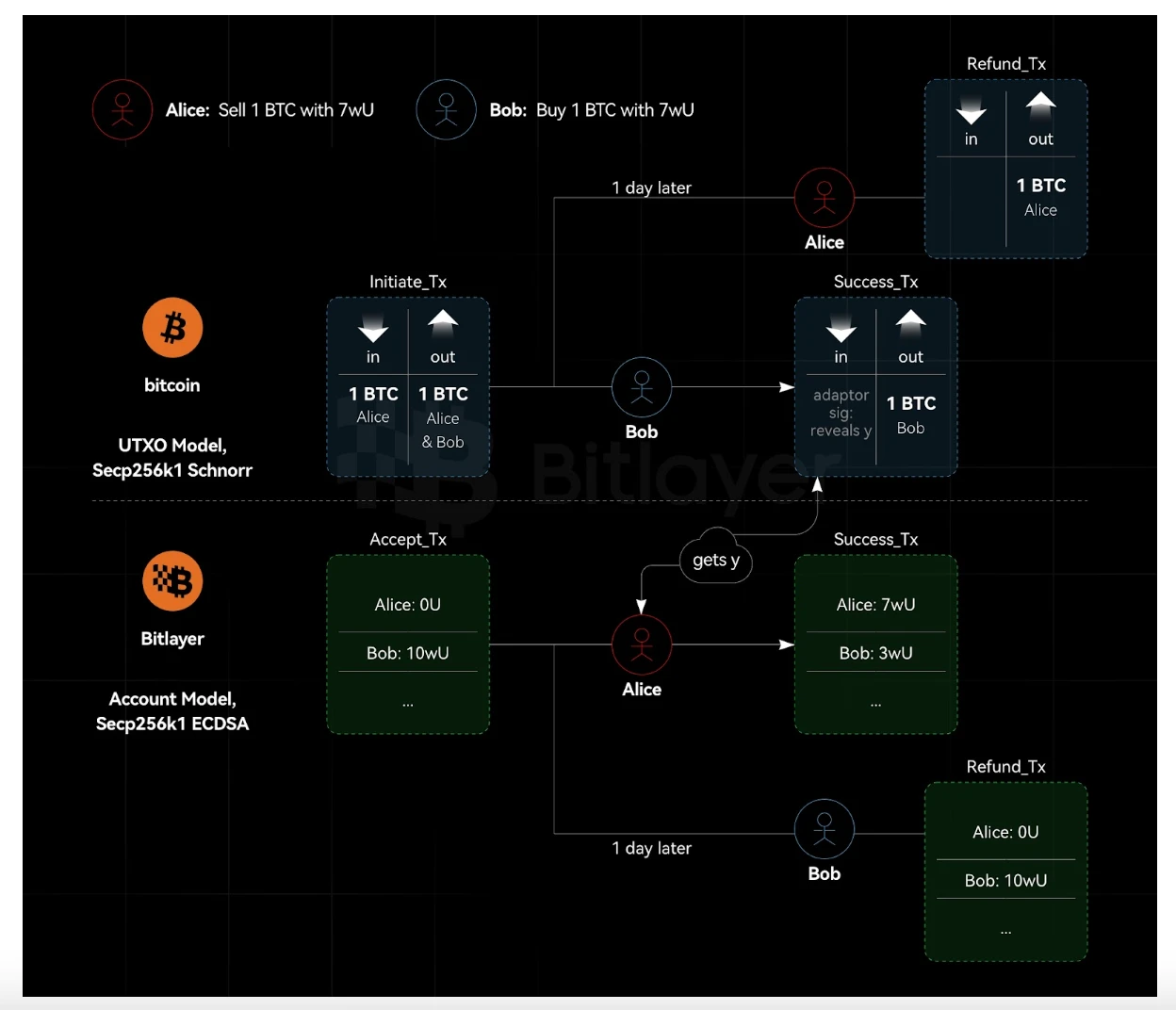
Şekil 1'de gösterildiği gibi, Bitcoin UTXO modelini kullanır ve Secp 256k1 eğrisine dayalı yerel ECDSA imzalarını uygular. Bitlayer, Secp 256k1 eğrisini kullanan ve yerel ECDSA imzalarını destekleyen EVM uyumlu bir Bitcoin L2 zinciridir. Bağdaştırıcı imzası, BTC değişimi için gereken mantığı uygularken, Bitlayer değişim karşılığı, Ethereum akıllı sözleşmelerinin güçlü işlevleri tarafından desteklenir.

Adaptör imzalarına dayalı çapraz zincir atomik takaslar veya en azından ECDSA eğrileri için tasarlanmış yarı-betiksiz adaptör imza şemaları Ethereum ile uyumsuzdur. Bunun nedeni Ethereum'un bir UTXO modeli değil, bir hesap modeli olmasıdır. Özellikle, adaptör imza tabanlı atomik takaslar geri ödeme işlemlerinin önceden imzalanmasını gerektirir. Ancak, Ethereum sisteminde, işlemler nonce bilinmeden önceden imzalanamaz. Bu nedenle, bir taraf ön imzanın tamamlanması ile işlemin yürütülmesi arasında bir işlem gönderebilir - bu da önceden imzalanmış işlemi geçersiz kılar (çünkü nonce kullanılmıştır ve yeniden kullanılamaz).

Ek olarak, gizlilik açısından bu, Bitlayer takaslarının HTLC'lerden daha anonim olduğu anlamına gelir (sözleşme takastaki her iki taraf için de mevcuttur). Ancak, bir tarafın genel bir sözleşmeye sahip olması gerekliliği, Bitlayer takaslarını adaptör imzalarından daha az anonim hale getirir. Sözleşme olmadan, takas işlemi diğer işlemler gibi görünür. Ancak, EVM sözleşmesi olan tarafta, işlem açıkça bir varlık takası içindir. Bir tarafın genel bir sözleşmesi olmasına rağmen, karmaşık zincir analiz araçlarıyla bile bunu başka bir zincire kadar izlemek imkansızdır.

Şekil 1. UTXO ve hesap modeli heterojen sistem çapraz zincir atomik takası

Bitlayer şu anda yerel ECDSA imzalarını destekliyor ve akıllı sözleşmeler aracılığıyla Schnorr imza doğrulamasını da uygulayabiliyor. Yerel Bitlayer işlemleri kullanılıyorsa, atomik takaslardaki iade işlemleri önceden imzalanamaz; atomik takasları uygulamak için Bitlayer akıllı sözleşme işlemleri gereklidir. Ancak bu süreç gizliliği feda eder, yani Bitlayer sisteminde atomik takaslara katılan işlemler izlenebilir, ancak BTC sistemindeki işlemlere kadar izlenemez. Tornado Cash gibi Dapp uygulamaları, BTC ve Bitlayer arasındaki atomik takaslarda Bitlayer tarafındaki işlemler için gizlilik hizmetleri sağlamak üzere Bitlayer tarafında tasarlanabilir.

3.2.2 Aynı eğri, farklı algoritma, adaptör imza güvenliği

Şekil 2'de gösterildiği gibi, hem Bitcoin'in hem de Bitlayer'ın Secp 256 k 1 eğrisini kullandığını, ancak Bitcoin'in Schnorr imzalarını, Bitlayer'ın ise ECDSA kullandığını varsayalım. Bu durumda, Schnorr ve ECDSA'ya dayalı adaptör imzası kanıtlanabilir şekilde güvenlidir. ECDSA ve Schnorr imza kahinleri verildiğinde, ECDSA'yı kırmak için bir simülatör S oluşturulabileceğini, ardından yalnızca ECDSA imza kahinleri verildiğinde, ECDSA'yı kırmak için bir simülatör S oluşturulabileceğini varsayalım. Ancak, ECDSA güvenlidir. Benzer şekilde, ECDSA ve Schnorr imza kahinleri verildiğinde, Schnorr imzalarını kırmak için bir simülatör S oluşturulabileceğini, ardından yalnızca ECDSA imza kahinleri verildiğinde, Schnorr imzalarını kırmak için bir simülatör S oluşturulabileceğini varsayalım. Ancak, Schnorr imzaları güvenlidir. Bu nedenle, zincirler arası senaryoda, adaptör imzası aynı eğriyi kullanır, ancak imza algoritması farklıdır ve bu da güvenlidir. Başka bir deyişle, adaptör imzası bir ucun ECDSA'yı, diğer ucun ise Schnorr imzalarını kullanmasına olanak tanır.

Şekil 2. Aynı eğri, farklı algoritma, adaptör imzası

3.2.3 Farklı eğriler, güvenli olmayan bağdaştırıcı imzaları

Bitcoin'in Secp 256 k 1 eğrisi ve ECDSA imzasını, Bitlayer'ın ise ed 25519 eğrisi ve Schnorr imzasını kullandığını varsayalım. Bu durumda adaptör imzası kullanılamaz. Farklı eğriler nedeniyle eliptik eğri grubunun sırası farklıdır, yani modüler katsayı farklıdır. Bob, $y$'yi Bitcoin sistemindeki ECDSA imzasına uyarladığında $s:= ŝ+y$'yi hesaplar. Bu sırada $y$'nin değer alanı Secp 256 k 1 eliptik eğri grubunun skaler alanıdır. Daha sonra Alice'in ed 25519 eliptik eğri grubunda Schnorr imzasını gerçekleştirmek için $y$'yi kullanması gerekir. Ancak, ed 25519 eğrisinin kofaktörü 8'dir ve modüler katsayı Secp 256 k 1 eliptik eğri grubunun modüler katsayısına eşit değildir. Bu nedenle, ed 25519 eğrisinde Schnorr imzası gerçekleştirmek için $y$ kullanmak güvenli değildir.

4. Dijital varlık saklama uygulaması

Dijital varlık saklamada üç taraf vardır: Alıcı Alice, satıcı Bob ve muhafaza eden. Bağdaştırıcı imzalarını kullanmak, etkileşimsiz eşik dijital varlık saklamayı etkinleştirir ve etkileşim olmadan eşik harcama stratejilerinin bir alt kümesini örnekleştirir. Bu alt küme iki tür katılımcıdan oluşur: başlatmaya katılan katılımcılar ve başlatmaya katılmayan katılımcılar, ikincisine muhafaza eden denir. Muhafaza eden keyfi işlemleri imzalayamaz, ancak sırları yalnızca desteklenen taraflardan birine gönderir.

Bir yandan, muhafaza eden kişi yalnızca birkaç sabit yerleşim işlemi arasından seçim yapabilir ve diğer taraflardan biriyle yeni bir işlem imzalayamaz. Bu nedenle, bu gizli serbest bırakma mekanizması etkileşimsiz eşik muhafazasını eşik Schnorr imzasından daha az esnek hale getirir. Öte yandan, 3'te 2 harcama stratejisi eşik Schnorr imzası kullanılarak ayarlanabilir. Ancak, eşik Schnorr imza protokolü, merkezi olmayan bir anahtar üretim protokolünü çalıştırmak için üç taraf gerektirir. Bu nedenle, adaptör imzasına dayalı varlık muhafaza protokolünün etkileşimsiz olma avantajı vardır.

4.1 Bağdaştırıcı imzasına dayalı etkileşimsiz varlık saklama

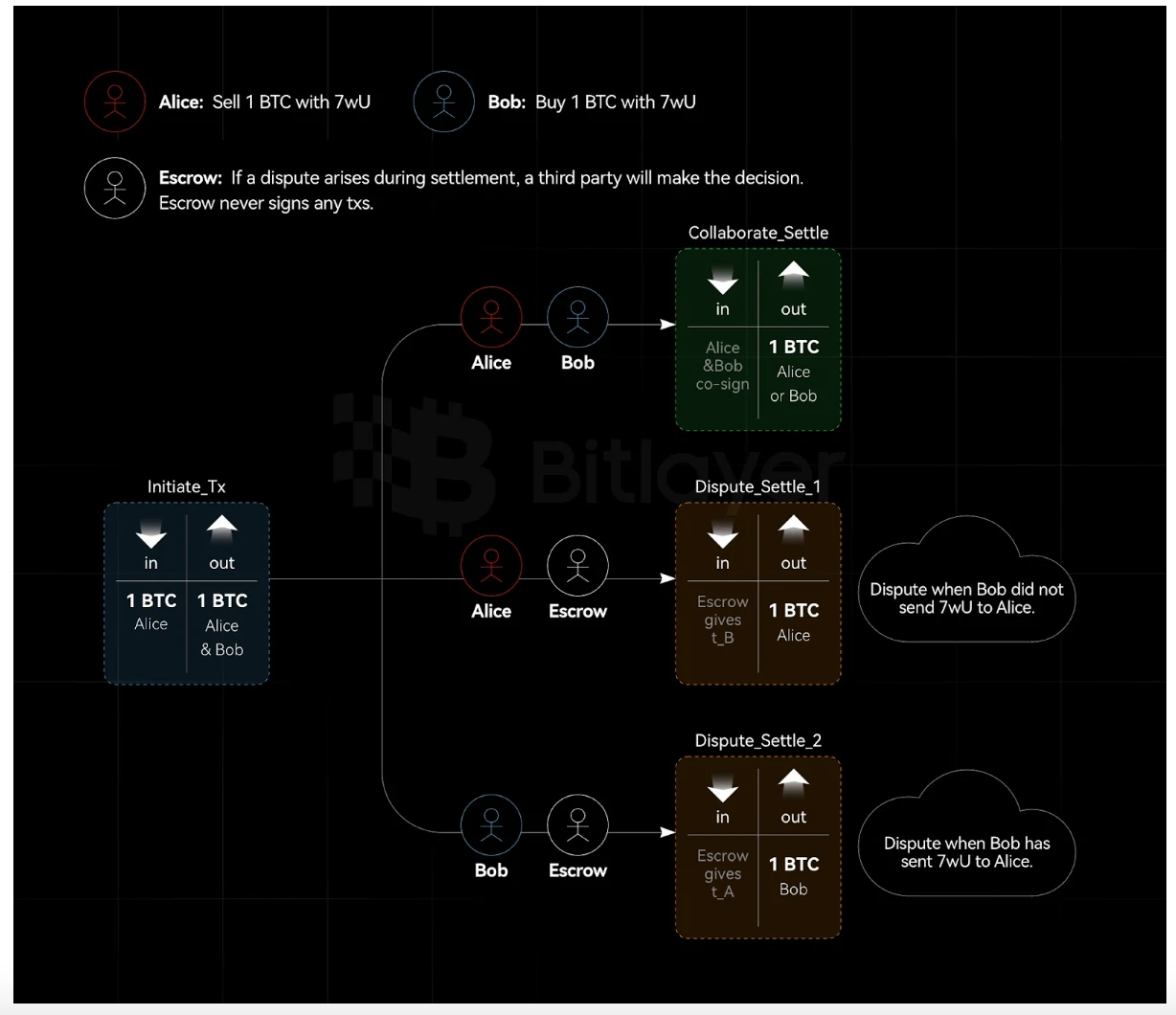
Şekil 3. Bağdaştırıcı imzasına dayalı etkileşimsiz varlık saklama

Şekil 3'te gösterildiği gibi, Alice ve Bob bir saklayıcı içeren gizli bir politika ile 2/3 işlem çıktısı oluşturmak ister. $c$ koşuluna bağlı olarak, Alice veya Bob işlem çıktısını harcayabilir. Alice ve Bob arasında bir anlaşmazlık varsa, saklayıcı (genel anahtar $E$, özel anahtar $e$'dir) Alice'in mi yoksa Bob'un mu varlığı alacağına karar verir.

• Alice ve Bob arasında 2'den 2'ye MuSig çıktısına BTC göndermek için imzasız bir fonlama işlemi oluşturun.

• Alice rastgele bir değer $t_A$ seçer ve $t_A ᐧ G$ bağdaştırıcısına sahip bir işlemin Schnorr ön imzası $(hat{R}_A,hat{s}_A)$'yi Bob'a gönderir. Bu işlem fonlama çıktısını Bob'a gönderir. Alice ayrıca Bob'a gizli $t_A$'nin doğrulanabilir şekilde şifrelenmiş $C = Enc(E_c, t_A)$'sini içeren bir şifreli metin gönderir ve emanet genel anahtarı $E$'yi $E_c = E + hash(E, c)G$ olarak ayarlar. Bu işlem sırasında, Bob Alice'in ön imzasını aldıktan sonra, 2-of-2 MuSig'i karşılamayan ve fonlama çıktısını harcayamayan kendi imzasını ekler. Finansman çıktısı yalnızca Bob'un $t_A$'yi (emanet tarafı tarafından sağlanan) bilmesi veya Alice'in tam bir imza atıp bunu Bob'a göndermesi durumunda harcanabilir.

• Buna uygun olarak, Bob, $t_B$ bağdaştırıcı sırrına dayanarak (2) adımını tekrarlar. Bu sırada, Bob tarafından imzalanan işlem, finansman çıktısını Alice'e gönderir.

• Alice ve Bob, alınan şifreli metnin geçerliliğini doğrular, şifreli metnin $E_c$ sırrının bir şifrelemesi olduğunu teyit eder ve ardından fonlama işlemini imzalar ve yayınlar. Doğrulanabilir şifreleme, bir saklayıcının kurulum aşamasına katılması ihtiyacını ortadan kaldırır ve $c$ genel sözleşmesi gerektirmez.

• Bir anlaşmazlık olduğunda, Alice ve Bob şifreli metni ve c koşulunu muhafaza eden kişiye gönderebilir, muhafaza eden kişi de gerçek duruma göre bir karar verebilir ve ayarlanmış özel anahtar $e+hash(E, c)$'yi kullanarak şifreyi çözebilir ve $t_A/t_B$'yi Bob/Alice'e gönderebilir.

Anlaşmazlık yoksa, Alice ve Bob 2'nin 2'sinin MuSig çıktısını istedikleri gibi harcayabilirler. Anlaşmazlık varsa, taraflardan biri muhafaza edenle iletişime geçip adaptör sırrı $t_A$ veya $t_B$'yi isteyebilir. Daha sonra, taraflardan biri muhafaza edenin yardımıyla adaptör imzasını tamamlayabilir ve yerleşim işlemini yayınlayabilir.

4.2 Doğrulanabilir Şifreleme

Ayrık Logaritmaların Pratik Doğrulanabilir Şifrelenmesi ve Şifresinin Çözülmesi Secp 256 k 1 adaptörleriyle kullanılamaz çünkü bunlar yalnızca özel olarak yapılandırılmış grupların doğrulanmasını destekler.

Şu anda, Secp 256k1 ayrık logaritmasına dayalı doğrulanabilir şifreleme yapmanın iki umut verici yolu vardır: Arındırmak Ve Jonglörlük .

Arındırmak başlangıçta, her imzalayanın, ortak anahtara ve mesaja bir sözde rastgele işlevi (PRF) doğru şekilde uygulamanın sonucu olan kendi nonce'larının sıfır bilgi kanıtı kullanmasını gerektiren, kesin bir nonce (DN) ile bir MuSig protokolü oluşturmak önerildi. Purify PRF, Bulletproofs sıfır bilgi protokolünün aritmetik devresinde Secp 256 k 1'de ayrı logaritmalar için doğrulanabilir bir şifreleme şeması oluşturmak için verimli bir şekilde uygulanabilir. Başka bir deyişle, doğrulanabilir şifreleme zkSnark kullanılarak elde edilir.

Jonglörlük Şifreleme dört adımdan oluşur: (1) Ayrık logaritmayı $x$, uzunluğu $l$ olan birden fazla $x_k$ segmentine bölün, böylece $x = sum _k 2 ^{(k-1)l} x_k$; (2) $x_k ᐧ G$ segmentinde ElGamal şifrelemesini gerçekleştirmek için $Y$ genel anahtarını kullanın; (3) $D_k$'nin bir Pedersen taahhüdü $x_k ᐧ G + r_k ᐧ Y$ olduğunu ve değerinin $ 2 ^l$'den küçük olduğunu kanıtlamak için her $x_k ᐧ G$ için bir aralık kanıtı oluşturun; (4) ${toplam D_k, toplam E_k}$'nin $x_k ᐧ G$'nin doğru şifrelemesi olduğunu kanıtlamak için sigma protokolünü kullanın.

Şifre çözme işlemi sırasında, her $x_k ᐧ G$'yi elde etmek için ${D_k, E_k}$ şifresi çözülür ve ardından $x_k$ ($[ 0, 2 ^l)$ değer aralığıyla) ayrıntılı olarak aranır.

Purify'ın Bulletproofs'ta bir PRF yürütmesi gerekir, bu da nispeten karmaşıktır, Juggling ise teorik olarak daha basittir. Ayrıca, ikisi arasındaki kanıt boyutu, kanıt süresi ve doğrulama süresi farkı çok küçüktür.

5. Sonuç

Bu makale Schnorr/ECDSA adaptör imzalarının ve zincirler arası atomik takasların prensiplerini ayrıntılı olarak açıklar. Adaptör imzalarının rastgele sayı sızıntısı ve çoğaltma sorunlarını derinlemesine analiz eder ve bu sorunları çözmek için RFC 6979'u kullanmayı önerir. Ayrıca, blok zincirinin UTXO modeli ile zincirler arası uygulama senaryolarındaki hesap modeli arasındaki farkları ayrıntılı olarak analiz eder ve adaptör imzasının farklı algoritmaları ve eğrileri destekleyip desteklemediğini de ele alır. Son olarak, adaptör imzası etkileşimsiz dijital varlık saklamayı gerçekleştirmek için genişletilir ve ilgili kriptografik ilkel - doğrulanabilir şifreleme kısaca tanıtılır.

referanslar

• Gugger J. Bitcoin-monero zincirler arası atomik takas[J]. Kriptoloji eBaskı Arşivi, 2020.

• Fournier L. Tek seferlik doğrulanabilir şifrelenmiş imzalar, diğer adıyla bağdaştırıcı imzaları[J]. 2019, 2019.

• https://crypto-in-action.github.io/ecdsa-blockchain-dangers/190816-secp256k1-ecdsa-dangers.pdf

• Pornin T. Dijital imza algoritması (DSA) ve eliptik eğri dijital imza algoritmasının (ECDSA)[R] deterministik kullanımı. 2013.

• Komlo C, Goldberg I. FROST: esnek tur optimize edilmiş Schnorr eşik imzaları[C]//Kriptografide Seçilmiş Alanlar: 27. Uluslararası Konferans, Halifax, NS, Kanada (Sanal Etkinlik), 21-23 Ekim 2020, Gözden Geçirilmiş Seçilmiş Makaleler 27. Springer International Publishing, 2021: 34-65.

• https://github.com/BlockstreamResearch/scriptless-scripts/blob/master/md/NITE.md

• https://particl.news/the-dex-revolution-basicswap-and-private-ethereum-swaps/

• Camenisch J, Shoup V. Ayrık logaritmaların pratik olarak doğrulanabilir şifrelenmesi ve şifresinin çözülmesi[C]//Yıllık Uluslararası Kriptoloji Konferansı. Berlin, Heidelberg: Springer Berlin Heidelberg, 2003: 126-144.

• Nick J, Ruffing T, Seurin Y, ve diğerleri. MuSig-DN: Doğrulanabilir kesin rastgele sayılara sahip Schnorr çoklu imzaları[C]//2020 ACM SIGSAC Bilgisayar ve İletişim Güvenliği Konferansı Bildirileri. 2020: 1717-1731.

• Shlomovits O, Leiba O. Jugglingswap: komut dosyası olmayan atomik zincirler arası takaslar[J].arXiv ön baskısı arXiv: 2007.14423, 2020.

Bu makale internetten alınmıştır: Bitcoin ve Layer2 varlık çapraz zincir teknolojisinin analizi

İlgili: Nakit dolu, Kaçış Ustası Warren Buffett'ın son 20 yıldaki parlak başarılarını değerlendirin

Orijinal başlık: Buffett'ın yine muhteşem hamlesi! Berkshire'ın nakit parası Ethereum'un piyasa değerini aştı, zirveden kaçışının 20 yıllık parlak sicilini gözden geçiriyor Orijinal yazar: James, BlockTempo Warren Buffett'a ait bir yatırım şirketi olan Berkshire Hathaway, geçen cumartesi günü 2024'ün ikinci çeyrek mali raporunu yayınladı ve şirketin 2. çeyrekte Apple hissesini yaklaşık 50% azalttığını ve nakit pozisyonunun $276,9 milyar ABD doları artarak yeni bir tarihi zirveye ulaştığını gösterdi. O zamanlar, bazı analistler Buffett'ın Apple hisselerindeki büyük satışının muhtemelen borsa ve ekonomik beklentiler hakkındaki karamsarlığından kaynaklandığına inanıyordu, bu yüzden nakitle her şeyi riske atmayı seçti. Şimdi, son günlerde ABD ve Asya borsalarının çökmesiyle birlikte, topluluk bir kez daha Buffett'ın zirveden başarıyla kaçışındaki zekasına hayranlık duyuyor. İlginçtir ki,…