Vitalik: Binius การพิสูจน์ประสิทธิภาพสำหรับเขตข้อมูลไบนารี

บทความต้นฉบับโดย: Vitalik Buterin

ต้นฉบับแปล: Kate, MarsBit

โพสต์นี้มีไว้สำหรับผู้อ่านที่โดยทั่วไปคุ้นเคยกับการเข้ารหัสในยุค 2019 และโดยเฉพาะ SNARK และ STARK หากคุณไม่ใช่ฉันขอแนะนำให้อ่านสิ่งเหล่านั้นก่อน ขอขอบคุณเป็นพิเศษสำหรับ Justin Drake, Jim Posen, Benjamin Diamond และ Radi Cojbasic สำหรับคำติชมและความคิดเห็น

Over the past two years, STARKs have become a key and irreplaceable technology for efficiently making easily verifiable cryptographic proofs of very complex statements (e.g. proving that an Ethereum block is valid). One of the key reasons for this is the small field size: SNARKs based on elliptic curves require you to work on 256-bit integers to be secure enough, while STARKs allow you to use much smaller field sizes with greater efficiency: first the Goldilocks field (64-bit integer), then Mersenne 31 and BabyBear (both 31 bits). Due to these efficiency gains, Plonky 2 using Goldilocks is hundreds of times faster than its predecessors at proving many kinds of computations.

คำถามทั่วไปก็คือ เราจะนำแนวโน้มนี้ไปสู่ข้อสรุปเชิงตรรกะและสร้างระบบพิสูจน์ที่ทำงานเร็วขึ้นโดยดำเนินการโดยตรงกับศูนย์และค่าศูนย์ได้หรือไม่ นี่คือสิ่งที่ Binius พยายามทำจริงๆ โดยใช้เทคนิคทางคณิตศาสตร์หลายอย่างที่ทำให้แตกต่างจาก SNARK และ STARK เมื่อสามปีที่แล้วอย่างมาก โพสต์นี้จะอธิบายว่าเหตุใดฟิลด์ขนาดเล็กจึงทำให้การสร้างการพิสูจน์มีประสิทธิภาพมากขึ้น เหตุใดฟิลด์ไบนารีจึงทรงพลังอย่างมีเอกลักษณ์ และเทคนิคที่ Binius ใช้เพื่อสร้างการพิสูจน์ในฟิลด์ไบนารีที่มีประสิทธิภาพมาก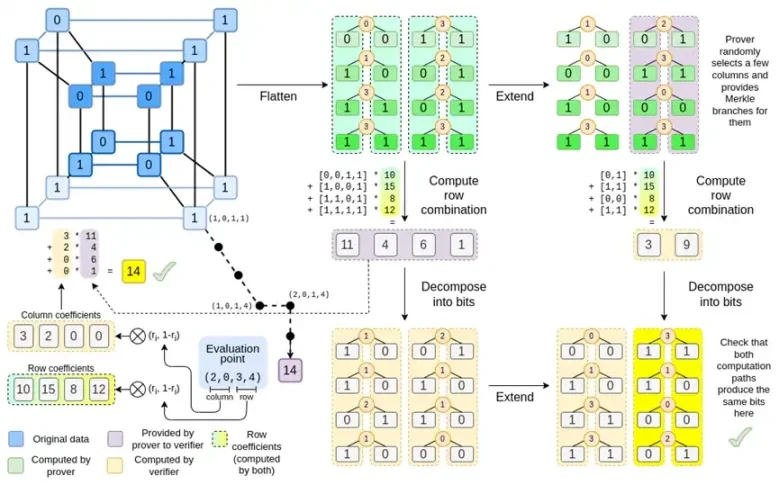

Binius ในตอนท้ายของโพสต์นี้ คุณควรจะสามารถเข้าใจทุกส่วนของแผนภาพนี้ได้

ทบทวน: เขตข้อมูลจำกัด

งานหลักประการหนึ่งของระบบพิสูจน์การเข้ารหัสคือการดำเนินการกับข้อมูลจำนวนมากโดยรักษาตัวเลขให้น้อย หากคุณสามารถบีบอัดคำสั่งเกี่ยวกับโปรแกรมขนาดใหญ่ให้เป็นสมการทางคณิตศาสตร์ที่มีตัวเลขไม่กี่ตัวได้ แต่ตัวเลขเหล่านั้นมีขนาดใหญ่เท่ากับโปรแกรมดั้งเดิม คุณจะไม่ได้อะไรเลย

ในการทำเลขคณิตที่ซับซ้อนในขณะที่รักษาตัวเลขให้เล็ก นักเข้ารหัสมักใช้เลขคณิตแบบโมดูลาร์ เราเลือกโมดูลัส p ของจำนวนเฉพาะ ตัวดำเนินการ % หมายถึงหาเศษ: 15% 7 = 1, 53% 10 = 3 และอื่นๆ (โปรดทราบว่าคำตอบนั้นไม่เป็นลบเสมอ เช่น -1% 10 = 9)

คุณอาจเคยเห็นเลขคณิตแบบโมดูลาร์ในบริบทของการบวกและการลบเวลา (เช่น เวลา 4 ชั่วโมงหลัง 9 โมง?) แต่ที่นี่ เราไม่เพียงแค่บวกและลบตัวเลขแบบโมดูโลเท่านั้น เรายังสามารถคูณ หาร และหาเลขยกกำลังได้ด้วย

เรากำหนดใหม่: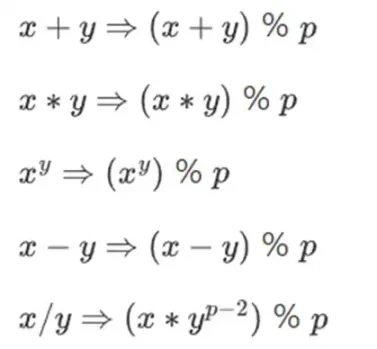

กฎข้างต้นทั้งหมดสอดคล้องกันในตัวเอง ตัวอย่างเช่น ถ้า p = 7 แล้ว:

5 + 3 = 1 (เพราะ 8% 7 = 1)

1-3 = 5 (เพราะ -2% 7 = 5)

2* 5 = 3

3/5 = 2

คำที่กว้างกว่าสำหรับโครงสร้างดังกล่าวคือเขตข้อมูลจำกัด สนามจำกัดคือโครงสร้างทางคณิตศาสตร์ที่เป็นไปตามกฎทางคณิตศาสตร์ตามปกติ แต่จำนวนค่าที่เป็นไปได้มีจำกัด เพื่อให้แต่ละค่าสามารถแสดงด้วยขนาดคงที่ได้

เลขคณิตแบบโมดูลาร์ (หรือเขตข้อมูลเฉพาะ) เป็นประเภทที่พบบ่อยที่สุดของเขตข้อมูลจำกัด แต่มีอีกประเภทหนึ่ง: เขตข้อมูลส่วนขยาย คุณอาจเคยเห็นฟิลด์ส่วนขยายหนึ่งฟิลด์: จำนวนเชิงซ้อน เราจินตนาการถึงองค์ประกอบใหม่และตั้งชื่อมันว่า i และคำนวณองค์ประกอบนั้น: (3i+2)*(2i+4)=6i*i+12i+4i+8=16i+2 เราก็ทำเช่นเดียวกันกับการขยายสนามเฉพาะได้ เมื่อเราเริ่มจัดการกับฟิลด์ที่มีขนาดเล็กลง ส่วนขยายของฟิลด์หลักมีความสำคัญมากขึ้นในด้านความปลอดภัย และฟิลด์ไบนารี (ใช้โดย Binius) อาศัยส่วนขยายทั้งหมดเพื่อให้มีประโยชน์ในทางปฏิบัติ

ทบทวน: การคำนวณทางคณิตศาสตร์

วิธีที่ SNARK และ STARK พิสูจน์ว่าโปรแกรมคอมพิวเตอร์นั้นใช้วิธีทางคณิตศาสตร์: คุณใช้คำสั่งเกี่ยวกับโปรแกรมที่คุณต้องการพิสูจน์ แล้วแปลงให้เป็นสมการทางคณิตศาสตร์ที่เกี่ยวข้องกับพหุนาม วิธีแก้สมการที่ถูกต้องสอดคล้องกับการทำงานของโปรแกรมที่ถูกต้อง

ตัวอย่างง่ายๆ สมมติว่าฉันคำนวณเลขฟีโบนัชชีลำดับที่ 100 และฉันต้องการพิสูจน์ให้คุณเห็นว่ามันคืออะไร ฉันสร้างพหุนาม F ที่เข้ารหัสลำดับฟีโบนักชี: ดังนั้น F(0)=F(1)=1, F(2)=2, F(3)=3, F(4)=5 และต่อๆ ไปเป็นเวลา 100 ขั้นตอน . เงื่อนไขที่ฉันต้องพิสูจน์คือ F(x+2)=F(x)+F(x+1) ตลอดช่วง x={0, 1…98} ฉันสามารถโน้มน้าวคุณได้โดยให้ผลหารแก่คุณ:

โดยที่ Z(x) = (x-0) * (x-1) * …(x-98) - หากฉันสามารถระบุได้ว่า F และ H เป็นไปตามสมการนี้ F จะต้องเป็นไปตาม F(x+ 2)-F(x+ 1)-F(x) ในช่วง หากฉันตรวจสอบเพิ่มเติมว่าสำหรับ F, F(0)=F(1)=1 แล้ว F(100) จะต้องเป็นเลขฟีโบนัชชีตัวที่ 100

หากคุณต้องการพิสูจน์บางสิ่งที่ซับซ้อนกว่านี้ ให้แทนที่ความสัมพันธ์แบบง่าย F(x+2) = F(x) + F(x+1) ด้วยสมการที่ซับซ้อนกว่าที่โดยพื้นฐานแล้วบอกว่า F(x+1) คือผลลัพธ์ ในการเริ่มต้นเครื่องเสมือนด้วยสถานะ F(x) และรันขั้นตอนการคำนวณหนึ่งขั้นตอน คุณยังสามารถแทนที่ตัวเลข 100 ด้วยตัวเลขที่มากกว่าได้ เช่น 100000000 เพื่อรองรับขั้นตอนที่มากขึ้น

SNARK และ STARK ทั้งหมดมีพื้นฐานมาจากแนวคิดในการใช้สมการง่ายๆ เหนือพหุนาม (และบางครั้งเวกเตอร์และเมทริกซ์) เพื่อแสดงความสัมพันธ์จำนวนมากระหว่างค่าแต่ละค่า อัลกอริธึมบางประเภทไม่ได้ตรวจสอบความเท่าเทียมกันระหว่างขั้นตอนการคำนวณที่อยู่ติดกันดังที่กล่าวมาข้างต้น ตัวอย่างเช่น PLONK จะไม่ตรวจสอบ และ R1CS ก็เช่นกัน แต่การตรวจสอบที่มีประสิทธิภาพมากที่สุดหลายๆ รายการก็ทำเช่นนั้น เนื่องจากเป็นการง่ายกว่าที่จะลดค่าใช้จ่ายให้เหลือน้อยที่สุดโดยดำเนินการตรวจสอบเดียวกัน (หรือตรวจสอบสองสามครั้งเหมือนกัน) หลายๆ ครั้ง

Plonky 2: จาก SNARK และ STARK 256 บิต ไปจนถึง 64 บิต... มีเพียง STARK เท่านั้น

เมื่อห้าปีที่แล้ว บทสรุปที่สมเหตุสมผลของการพิสูจน์ความรู้เป็นศูนย์ประเภทต่างๆ มีดังนี้ การพิสูจน์มีสองประเภท: (ตามเส้นโค้งรูปไข่) SNARK และ (ตามแฮช) STARK ในทางเทคนิค STARK เป็น SNARK ประเภทหนึ่ง แต่ในทางปฏิบัติ เป็นเรื่องปกติที่จะใช้ “SNARK” เพื่ออ้างถึงตัวแปรที่อิงตามเส้นโค้งวงรี และใช้ “STARK” เพื่ออ้างถึงโครงสร้างที่อิงแฮช SNARK มีขนาดเล็ก ดังนั้นคุณสามารถตรวจสอบได้อย่างรวดเร็วและติดตั้งออนไลน์ได้อย่างง่ายดาย STARK มีขนาดใหญ่ แต่ไม่ต้องการการตั้งค่าที่เชื่อถือได้ และทนทานต่อควอนตัม

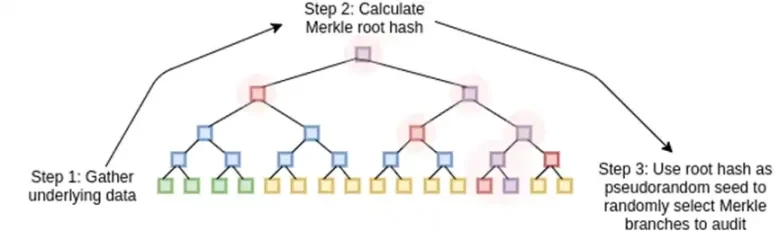
STARK ทำงานโดยถือว่าข้อมูลเป็นแบบพหุนาม คำนวณการคำนวณของพหุนามนั้น และใช้ราก Merkle ของข้อมูลที่ขยายเป็น "ความมุ่งมั่นแบบพหุนาม"

ประวัติความเป็นมาที่สำคัญที่นี่คือ SNARK ที่ใช้เส้นโค้งรูปไข่ถูกนำมาใช้อย่างกว้างขวางก่อน: STARK ไม่ได้มีประสิทธิภาพเพียงพอจนกระทั่งประมาณปี 2018 ต้องขอบคุณ FRI และเมื่อถึงเวลานั้น Zcash ก็เปิดใช้งานมานานกว่าหนึ่งปี SNARK ที่ใช้เส้นโค้งวงรีมีข้อจำกัดที่สำคัญ: หากคุณต้องการใช้ SNARK ที่ใช้เส้นโค้งวงรี เลขคณิตในสมการเหล่านี้จะต้องทำแบบโมดูโลกับจำนวนจุดบนเส้นโค้งวงรี นี่เป็นตัวเลขจำนวนมาก ซึ่งมักจะใกล้กับ 2 ยกกำลัง 256 เช่น สำหรับเส้นโค้ง bn128 มันคือ 21888242871839275222246405745257275088548364400416034343698204186575808495617 แต่การคำนวณจริงจะใช้จำนวนน้อย ถ้าคุณคิด เกี่ยวกับโปรแกรมจริงในภาษาที่คุณชื่นชอบ เกือบทุกอย่าง การใช้งานเป็นตัวนับ ดัชนีในลูป ตำแหน่งในโปรแกรม บิตเดี่ยวที่แสดงถึง True หรือ False และสิ่งอื่นๆ ที่มักจะมีความยาวเพียงไม่กี่หลักเท่านั้น

แม้ว่าข้อมูลต้นฉบับของคุณจะประกอบด้วยจำนวนน้อย แต่กระบวนการพิสูจน์ต้องใช้ผลหารในการคำนวณ การขยาย การรวมกันเชิงเส้นแบบสุ่ม และการแปลงข้อมูลอื่นๆ ที่จะส่งผลให้มีออบเจ็กต์จำนวนเท่ากันหรือมากขึ้น ซึ่งโดยเฉลี่ยมีขนาดใหญ่เท่ากับขนาดเต็มของออบเจ็กต์ของคุณ สนาม. สิ่งนี้ทำให้เกิดความไร้ประสิทธิภาพที่สำคัญ: เพื่อพิสูจน์การคำนวณด้วยค่าที่น้อย คุณจะต้องทำการคำนวณอีกหลายครั้งด้วยค่าที่มากกว่า n ค่าที่มากกว่ามาก ในตอนแรก STARK สืบทอดนิสัย SNARK ในการใช้ฟิลด์ 256 บิต และด้วยเหตุนี้จึงประสบปัญหาจากความไร้ประสิทธิภาพเช่นเดียวกัน

การขยายตัวของรีด-โซโลมอนของการประเมินพหุนามบางส่วน แม้ว่าค่าเดิมจะมีน้อย ค่าเพิ่มเติมจะถูกขยายจนเต็มขนาดฟิลด์ (ในกรณีนี้ 2^31 – 1)

ในปี 2022 Plonky 2 ได้รับการปล่อยตัว นวัตกรรมหลักของ Plonky 2 คือการใช้เลขคณิตแบบโมดูโลกับจำนวนเฉพาะที่น้อยกว่า: 2 ยกกำลัง 64 – 2 ยกกำลัง 32 + 1 = 18446744067414584321 ในตอนนี้ การบวกหรือการคูณแต่ละครั้งสามารถทำได้โดยใช้คำแนะนำเพียงไม่กี่ข้อบน CPU และการแฮชข้อมูลทั้งหมดเข้าด้วยกันเร็วกว่าเดิมถึง 4 เท่า แต่มีปัญหาอยู่: วิธีนี้ใช้ได้กับ STARK เท่านั้น หากคุณพยายามใช้ SNARK เส้นโค้งวงรีจะไม่ปลอดภัยสำหรับเส้นโค้งวงรีขนาดเล็กดังกล่าว

เพื่อความมั่นใจในความปลอดภัย Plonky 2 จำเป็นต้องแนะนำฟิลด์ส่วนขยายด้วย เทคนิคสำคัญในการตรวจสอบสมการทางคณิตศาสตร์คือการสุ่มตัวอย่างจุด: หากคุณต้องการตรวจสอบว่า H(x) * Z(x) เท่ากับ F(x+ 2)-F(x+ 1)-F(x) คุณสามารถสุ่มได้ เลือกพิกัด r จัดให้มีความมุ่งมั่นพหุนามเพื่อพิสูจน์ H(r), Z(r), F(r), F(r+ 1) และ F(r+ 2) จากนั้นตรวจสอบว่า H(r) * Z(r ) เท่ากับ F(r+ 2)-F(r+ 1)- F(r) หากผู้โจมตีสามารถเดาพิกัดล่วงหน้าได้ ผู้โจมตีก็สามารถหลอกลวงระบบพิสูจน์อักษรได้ ด้วยเหตุนี้ระบบพิสูจน์จึงต้องสุ่ม แต่นี่ก็หมายความว่าพิกัดจะต้องสุ่มตัวอย่างจากชุดที่มีขนาดใหญ่เพียงพอที่ผู้โจมตีไม่สามารถคาดเดาแบบสุ่มได้ สิ่งนี้จะเป็นจริงอย่างเห็นได้ชัดหากโมดูลัสใกล้กับ 2 ยกกำลัง 256 อย่างไรก็ตาม สำหรับโมดูลัส 2^64 - 2^32 + 1 เรายังไปไม่ถึง และจะไม่เป็นเช่นนั้นอย่างแน่นอนหากเราลงไปถึง 2^31 – 1. ผู้โจมตีสามารถปลอมแปลงหลักฐานสองพันล้านครั้งจนกว่าจะโชคดี

เพื่อป้องกันสิ่งนี้ เราสุ่มตัวอย่าง r จากช่องขยาย ตัวอย่างเช่น คุณสามารถกำหนด y โดยที่ y^3 = 5 และนำ 1, y และ y^2 มารวมกัน ทำให้จำนวนพิกัดทั้งหมดอยู่ที่ประมาณ 2^93 พหุนามส่วนใหญ่ที่คำนวณโดยสุภาษิตไม่ได้อยู่ในสาขาขยายนี้ พวกมันเป็นเพียงจำนวนเต็มโมดูโล 2^31-1 ดังนั้นคุณยังคงได้รับประสิทธิภาพทั้งหมดจากการใช้สนามขนาดเล็ก แต่การตรวจสอบจุดสุ่มและการคำนวณ FRI จะเข้าถึงฟิลด์ที่ใหญ่กว่านี้เพื่อรับความปลอดภัยที่ต้องการ

จากจำนวนเฉพาะน้อยไปจนถึงเลขฐานสอง

คอมพิวเตอร์คำนวณเลขคณิตโดยแสดงตัวเลขที่มากขึ้นเป็นลำดับของ 0 และ 1 และสร้างวงจรไว้บนบิตเหล่านั้นเพื่อคำนวณการดำเนินการ เช่น การบวกและการคูณ คอมพิวเตอร์ได้รับการปรับให้เหมาะสมเป็นพิเศษสำหรับจำนวนเต็ม 16-, 32- และ 64 บิต ตัวอย่างเช่น 2^64 – 2^32 + 1 และ 2^31 – 1 ถูกเลือกไม่เพียงเพราะมันพอดีกับขอบเขตเหล่านั้น แต่ยังเพราะมันเข้ากันได้ดีภายในขอบเขตเหล่านั้นด้วย: การคูณแบบโมดูโล 2^64 – 2^32 + 1 สามารถทำได้โดยการคูณแบบ 32 บิตปกติ และเลื่อนระดับบิตและคัดลอกเอาต์พุตในบางแห่ง บทความนี้จะอธิบายเทคนิคบางอย่างอย่างดี

อย่างไรก็ตาม วิธีที่ดีกว่ามากคือการคำนวณโดยตรงในรูปแบบไบนารี จะเกิดอะไรขึ้นถ้าการบวกอาจเป็นเพียง XOR โดยไม่ต้องกังวลกับการบวก 1 + 1 จากบิตหนึ่งไปยังบิตถัดไป จะเกิดอะไรขึ้นถ้าการคูณสามารถขนานกันมากขึ้นในลักษณะเดียวกันได้? ข้อดีเหล่านี้ทั้งหมดขึ้นอยู่กับความสามารถในการแสดงค่าจริง/เท็จด้วยบิตเดียว

การได้รับข้อดีเหล่านี้จากการคำนวณไบนารี่โดยตรงคือสิ่งที่ Binius พยายามทำ ทีม Binius สาธิตประสิทธิภาพที่เพิ่มขึ้นในการนำเสนอที่ zkSummit:

แม้ว่าจะมีขนาดใกล้เคียงกัน แต่การดำเนินการบนฟิลด์ไบนารี 32 บิตต้องใช้ทรัพยากรในการคำนวณน้อยกว่าการดำเนินการบนฟิลด์ Mersenne 31 บิตถึง 5 เท่า

จากพหุนามที่ไม่แปรเปลี่ยนไปจนถึงไฮเปอร์คิวบ์

สมมติว่าเราเชื่อเหตุผลนี้ และต้องการทำทุกอย่างด้วยบิต (0 และ 1) เราจะแสดงพันล้านบิตด้วยพหุนามเดียวได้อย่างไร

ที่นี่เราประสบปัญหาในทางปฏิบัติสองประการ:

1. เพื่อให้พหุนามแสดงค่าจำนวนมาก ค่าเหล่านี้จำเป็นต้องสามารถเข้าถึงได้เมื่อประเมินพหุนาม: ในตัวอย่างฟีโบนัชชีด้านบน F(0), F(1) … F(100) และในการคำนวณที่มากขึ้น เลขชี้กำลังจะเป็นหลักล้าน ฟิลด์ที่เราใช้ต้องมีตัวเลขขนาดนี้

2. การพิสูจน์ค่าใดๆ ที่เรากระทำในแผนผัง Merkle (เช่นเดียวกับ STARK ทั้งหมด) จำเป็นต้องมีการเข้ารหัส Reed-Solomon เช่น การขยายค่าจาก n เป็น 8n โดยใช้การซ้ำซ้อนเพื่อป้องกันไม่ให้ผู้พิสูจน์เจตนาร้ายทำการโกงโดยการสร้างค่าระหว่างการคำนวณ นอกจากนี้ยังจำเป็นต้องมีฟิลด์ที่ใหญ่เพียงพอ: ในการขยายจากค่าล้านค่าเป็น 8 ล้าน คุณต้องมีจุดที่แตกต่างกัน 8 ล้านจุดเพื่อประเมินพหุนาม

แนวคิดหลักของ Binius คือการแก้ปัญหาทั้งสองนี้แยกกัน และดำเนินการดังกล่าวด้วยการแสดงข้อมูลเดียวกันในสองวิธีที่แตกต่างกัน ประการแรก พหุนามนั้นเอง ระบบต่างๆ เช่น SNARK ที่ใช้เส้นโค้งรูปไข่, STARK ในยุค 2019, Plonky 2 และอื่นๆ โดยทั่วไปจะจัดการกับพหุนามในตัวแปรตัวเดียว: F(x) ในทางกลับกัน Binius ได้รับแรงบันดาลใจจากโปรโตคอล Spartan และใช้พหุนามหลายตัวแปร: F(x 1, x 2,… xk) โดยพื้นฐานแล้ว เราแสดงวิถีการคำนวณทั้งหมดบนไฮเปอร์คิวบ์ของการคำนวณ โดยที่ xi แต่ละตัวเป็น 0 หรือ 1 ตัวอย่างเช่น หากเราต้องการแสดงลำดับฟีโบนัชชี และเรายังคงใช้ช่องที่ใหญ่พอที่จะแสดงลำดับฟีโบนัชชี เราก็สามารถ ลองนึกภาพ 16 ลำดับแรกของพวกเขาดังนี้: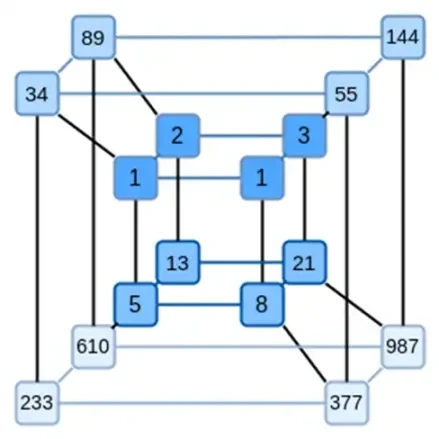

นั่นคือ F(0,0,0,0) ควรเป็น 1, F(1,0,0,0) เท่ากับ 1, F(0,1,0,0) คือ 2 และต่อๆ ไป จนถึง F(1,1,1,1) = 987 เมื่อพิจารณาถึงไฮเปอร์คิวบ์ของการคำนวณดังกล่าว จะมีพหุนามเชิงเส้นหลายตัวแปร (ระดับ 1 ในแต่ละตัวแปร) ที่สร้างการคำนวณเหล่านี้ ดังนั้นเราจึงคิดว่าชุดค่านี้เป็นตัวแทนของพหุนามได้ เราไม่จำเป็นต้องคำนวณสัมประสิทธิ์

แน่นอนว่าตัวอย่างนี้เป็นเพียงภาพประกอบเท่านั้น ในทางปฏิบัติ จุดรวมของการเข้าสู่ไฮเปอร์คิวบ์คือให้เราจัดการกับแต่ละบิต วิธีคำนวณเลขฟีโบนัชชีแบบพื้นเมืองของ Binius คือการใช้คิวบ์ที่มีมิติสูงกว่า โดยจัดเก็บหนึ่งหมายเลขต่อกลุ่ม เช่น 16 บิต สิ่งนี้ต้องใช้ความฉลาดบางประการในการบวกจำนวนเต็มเพียงเล็กน้อย แต่สำหรับ Binius มันไม่ยากเกินไป

ตอนนี้เรามาดูรหัสการลบ วิธีการทำงานของ STARK คือคุณรับค่า n ค่า รีด-โซโลมอนจะขยายค่าเหล่านั้นเป็นค่าที่มากขึ้น (ปกติจะเป็น 8n ซึ่งโดยปกติจะอยู่ระหว่าง 2n ถึง 32n) จากนั้นสุ่มเลือกสาขา Merkle บางสาขาจากส่วนขยาย และทำการตรวจสอบบางอย่างกับค่าเหล่านั้น ไฮเปอร์คิวบ์มีความยาว 2 ในแต่ละมิติ ดังนั้นจึงไม่เหมาะสมที่จะขยายโดยตรง: ไม่มีพื้นที่เพียงพอที่จะสุ่มตัวอย่างสาขา Merkle จาก 16 ค่า แล้วเราจะทำอย่างไร? สมมติว่าไฮเปอร์คิวบ์เป็นสี่เหลี่ยมจัตุรัส!

Simple Binius – ตัวอย่าง

ดู ที่นี่ สำหรับการนำโปรโตคอลไปใช้หลาม

ลองดูตัวอย่าง โดยใช้จำนวนเต็มปกติเป็นฟิลด์ของเราเพื่อความสะดวก (ในการใช้งานจริง เว้นส์เดย์ใช้องค์ประกอบฟิลด์ไบนารี) ขั้นแรก เราเข้ารหัสไฮเปอร์คิวบ์ที่เราต้องการส่งเป็นสี่เหลี่ยมจัตุรัส:

ตอนนี้เราขยายกำลังสองโดยใช้วิธีรีด-โซโลมอน นั่นคือ เราถือว่าแต่ละแถวเป็นพหุนามระดับ 3 ที่ x = { 0, 1, 2, 3 } และประเมินพหุนามเดียวกันที่ x = { 4, 5, 6, 7 }: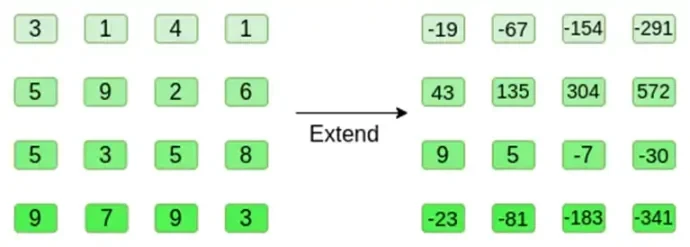

โปรดทราบว่าตัวเลขอาจมีขนาดใหญ่มาก! นี่คือเหตุผลว่าทำไมในการใช้งานจริง เรามักจะใช้ฟิลด์จำกัด แทนที่จะเป็นจำนวนเต็มปกติ เช่น หากเราใช้จำนวนเต็มโมดูโล 11 การขยายตัวของแถวแรกจะเป็น [3, 10, 0, 6]

หากคุณต้องการลองใช้ส่วนขยายและยืนยันตัวเลขด้วยตนเอง คุณสามารถใช้โค้ดส่วนขยาย Reed-Solomon แบบง่ายๆ ของฉันได้ที่นี่

ต่อไป เราจะถือว่าส่วนขยายนี้เป็นคอลัมน์และสร้างแผนผัง Merkle ของคอลัมน์ รากฐานของต้น Merkle คือความมุ่งมั่นของเรา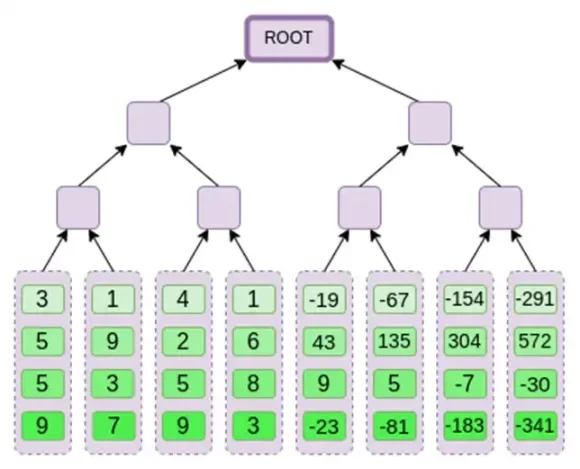

ทีนี้ สมมติว่าผู้พิสูจน์ต้องการพิสูจน์การคำนวณของพหุนาม r = {r 0, r 1, r 2, r 3 } ณ จุดใดจุดหนึ่ง มีความแตกต่างเล็กน้อยใน Binius ซึ่งทำให้อ่อนแอกว่าแผนการผูกมัดพหุนามอื่นๆ: ผู้พิสูจน์ไม่ควรรู้หรือไม่สามารถเดา s ก่อนที่จะตัดสินใจใช้ราก Merkle (กล่าวอีกนัยหนึ่ง r ควรเป็นค่าสุ่มหลอกที่ขึ้นอยู่กับ รากเมิร์เคิล) สิ่งนี้ทำให้รูปแบบไม่มีประโยชน์สำหรับการค้นหาฐานข้อมูล (เช่น ตกลง คุณให้ราก Merkle แก่ฉัน ตอนนี้พิสูจน์ให้ฉัน P(0, 0, 1, 0)!) แต่โปรโตคอลการพิสูจน์ความรู้เป็นศูนย์ที่เราใช้จริงมักไม่ต้องการการค้นหาฐานข้อมูล พวกเขาต้องการเพียงการตรวจสอบพหุนามที่จุดประเมินแบบสุ่มเท่านั้น ดังนั้นข้อจำกัดนี้จึงตอบสนองวัตถุประสงค์ของเราได้เป็นอย่างดี

สมมติว่าเราเลือก r = { 1, 2, 3, 4 } (ค่าพหุนามมีค่าเป็น -137 คุณสามารถยืนยันได้โดยใช้โค้ดนี้) ตอนนี้เรามาถึงการพิสูจน์ เราแบ่ง r ออกเป็นสองส่วน ส่วนแรก { 1, 2 } แสดงถึงผลรวมเชิงเส้นของคอลัมน์ภายในแถว และส่วนที่สอง { 3, 4 } แสดงถึงผลรวมเชิงเส้นของแถว เราคำนวณผลิตภัณฑ์เทนเซอร์และสำหรับคอลัมน์:

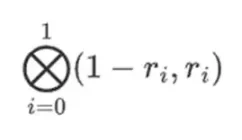
สำหรับส่วนของแถว:

ซึ่งหมายความว่า: รายการของผลิตภัณฑ์ที่เป็นไปได้ทั้งหมดของค่าในแต่ละชุด ในกรณีแถวเราได้รับ:

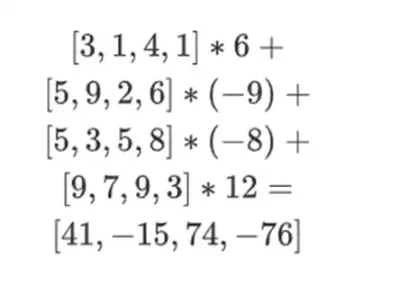
[( 1-r 2)*( 1-r 3), ( 1-r 3), ( 1-r 2)*r 3, R 2*r 3 ]

ด้วย r = { 1, 2, 3, 4 } (ดังนั้น r 2 = 3 และ r 3 = 4):

[( 1-3)*( 1-4), 3*( 1-4),( 1-3)* 4, 3* 4 ] = [ 6, -9 -8 -12 ]

ตอนนี้ เราคำนวณแถวใหม่ t โดยหาผลรวมเชิงเส้นของแถวที่มีอยู่ นั่นคือเราใช้:

คุณสามารถนึกถึงสิ่งที่เกิดขึ้นที่นี่เป็นการประเมินเพียงบางส่วนได้ หากเราคูณผลคูณเทนเซอร์เต็มด้วยเวกเตอร์เต็มของค่าทั้งหมด คุณจะได้ผลการคำนวณ P(1, 2, 3, 4) = -137 ที่นี่ เราได้คูณผลิตภัณฑ์เทนเซอร์บางส่วนโดยใช้เพียงครึ่งหนึ่งของพิกัดการประเมิน และลดตารางของค่า N เหลือแถวเดียวของค่ารากที่สองของค่า N หากคุณให้แถวนี้แก่ผู้อื่น พวกเขาสามารถคำนวณส่วนที่เหลือได้โดยใช้ผลคูณเทนเซอร์ของอีกครึ่งหนึ่งของพิกัดการประเมิน

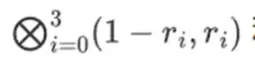
เครื่องพิสูจน์จัดเตรียมแถวใหม่ต่อไปนี้ให้ผู้ตรวจสอบ: t และการพิสูจน์ Merkle ของคอลัมน์สุ่มตัวอย่างบางคอลัมน์ ในตัวอย่างภาพประกอบของเรา เราจะให้สุภาษิตระบุเฉพาะคอลัมน์สุดท้ายเท่านั้น ในชีวิตจริง ผู้พิสูจน์จะต้องจัดเตรียมคอลัมน์หลายสิบคอลัมน์เพื่อให้เกิดความปลอดภัยที่เพียงพอ

ตอนนี้เราใช้ประโยชน์จากความเป็นเส้นตรงของรหัสรีด-โซโลมอน คุณสมบัติหลักที่เราใช้ประโยชน์คือการรวมเชิงเส้นของส่วนขยายรีด-โซโลมอน ให้ผลลัพธ์เช่นเดียวกับการขยายการขยายรีด-โซโลมอนของการรวมเชิงเส้น ความเป็นอิสระตามลำดับนี้มักเกิดขึ้นเมื่อการดำเนินการทั้งสองเป็นแบบเส้นตรง

ผู้ตรวจสอบทำสิ่งนั้นทุกประการ พวกเขาคำนวณ t และคำนวณชุดค่าผสมเชิงเส้นของคอลัมน์เดียวกันกับที่ผู้พิสูจน์อักษรเคยคำนวณไว้ก่อนหน้านี้ (แต่เฉพาะคอลัมน์ที่จัดเตรียมโดยผู้พิสูจน์อักษรเท่านั้น) และตรวจสอบว่าทั้งสองขั้นตอนให้คำตอบเดียวกัน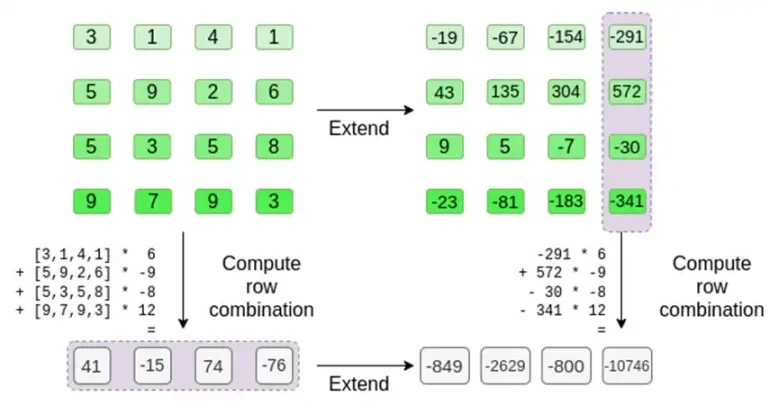

ในกรณีนี้ เราขยาย t และคำนวณผลรวมเชิงเส้นเดียวกัน ([6,-9,-8, 12]) ซึ่งทั้งคู่ให้คำตอบเดียวกัน: -10746 นี่เป็นการพิสูจน์ว่ารากของ Merkle ถูกสร้างขึ้นโดยสุจริต (หรืออย่างน้อยก็ใกล้เคียงเพียงพอ) และตรงกับ t: อย่างน้อยคอลัมน์ส่วนใหญ่ก็เข้ากันได้

แต่มีอีกสิ่งหนึ่งที่ผู้ตรวจสอบจำเป็นต้องตรวจสอบ: ตรวจสอบการประเมินของพหุนาม {r 0 …r 3 } ขั้นตอนทั้งหมดของผู้ตรวจสอบจนถึงขณะนี้ไม่ได้ขึ้นอยู่กับมูลค่าที่ผู้พิสูจน์อ้างสิทธิ์ นี่คือวิธีที่เราตรวจสอบ เราใช้ผลิตภัณฑ์เทนเซอร์ของ "ส่วนคอลัมน์" ที่เราทำเครื่องหมายว่าเป็นจุดคำนวณ: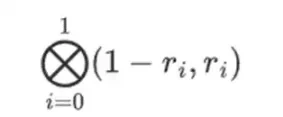

ในกรณีของเรา โดยที่ r = { 1, 2, 3, 4 } ดังนั้นครึ่งหนึ่งของคอลัมน์ที่เลือกคือ { 1, 2 }) นี่จะเท่ากับ:

ตอนนี้เราใช้ผลรวมเชิงเส้นนี้ t:

นี่เหมือนกับการแก้พหุนามโดยตรง

ข้อมูลข้างต้นใกล้เคียงกับคำอธิบายที่สมบูรณ์ของโปรโตคอล Binius แบบง่ายมาก สิ่งนี้มีข้อดีที่น่าสนใจอยู่แล้ว เช่น เนื่องจากข้อมูลถูกแยกออกเป็นแถวและคอลัมน์ คุณจึงต้องใช้ฟิลด์ที่มีขนาดเพียงครึ่งหนึ่งเท่านั้น อย่างไรก็ตาม สิ่งนี้ไม่ได้ให้ประโยชน์เต็มที่จากการคำนวณในรูปแบบไบนารี เพื่อสิ่งนั้น เราจำเป็นต้องมีโปรโตคอล Binius แบบเต็ม แต่ก่อนอื่น เรามาดูเขตข้อมูลไบนารีให้ลึกซึ้งยิ่งขึ้น

ฟิลด์ไบนารี

ฟิลด์ที่เล็กที่สุดเท่าที่จะเป็นไปได้คือโมดูโลเลขคณิต 2 ซึ่งมีขนาดเล็กมากจนเราสามารถเขียนตารางการบวกและสูตรคูณได้:

เราสามารถได้รับเขตข้อมูลไบนารีที่ใหญ่ขึ้นโดยการขยาย: ถ้าเราเริ่มต้นด้วย F 2 (จำนวนเต็มโมดูโล 2) แล้วกำหนด x โดยที่ x กำลังสอง = x + 1 เราจะได้ตารางการบวกและสูตรคูณต่อไปนี้:

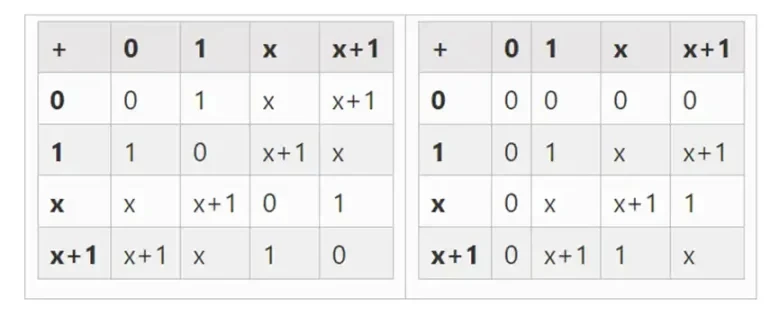
ปรากฎว่าเราสามารถขยายเขตข้อมูลไบนารี่ให้มีขนาดใหญ่ได้ตามใจชอบโดยการทำซ้ำโครงสร้างนี้ ต่างจากจำนวนเชิงซ้อนเหนือจำนวนจริง โดยที่คุณสามารถเพิ่มองค์ประกอบใหม่ได้แต่ไม่ต้องเพิ่มองค์ประกอบใดๆ อีกต่อไป I (ควอเทอร์เนียนมีอยู่จริง แต่พวกมันแปลกในทางคณิตศาสตร์ เช่น ab ไม่เท่ากับ ba) ด้วยช่องจำกัดที่คุณสามารถเพิ่มส่วนขยายใหม่ได้ ตลอดไป. โดยเฉพาะอย่างยิ่ง คำจำกัดความขององค์ประกอบของเรามีดังนี้: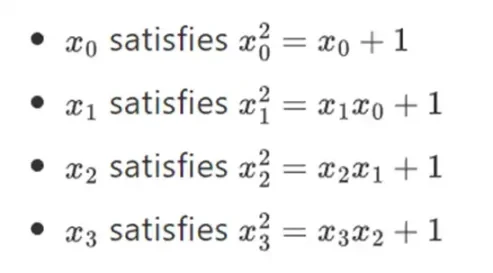

และอื่นๆ... สิ่งนี้มักเรียกว่าการก่อสร้างหอคอย เนื่องจากการขยายตัวต่อเนื่องแต่ละครั้งอาจถือเป็นการเพิ่มเลเยอร์ใหม่ให้กับหอคอย นี่ไม่ใช่วิธีเดียวที่จะสร้างเขตข้อมูลไบนารี่ที่มีขนาดตามใจชอบ แต่ก็มีข้อดีเฉพาะบางประการที่ Binius หาประโยชน์

เราสามารถแสดงตัวเลขเหล่านี้เป็นรายการบิตได้ ตัวอย่างเช่น 1100101010001111 บิตแรกแทนค่าทวีคูณของ 1 บิตที่สองแทนค่าทวีคูณของ x0 จากนั้นบิตต่อไปนี้แทนค่าทวีคูณของ x1: x1, x1*x0, x2, x2*x0 และอื่นๆ การเข้ารหัสนี้ดีเพราะคุณสามารถแยกย่อยได้:

นี่เป็นสัญลักษณ์ที่ค่อนข้างไม่ธรรมดา แต่ฉันชอบแสดงองค์ประกอบของสนามไบนารี่เป็นจำนวนเต็ม โดยมีบิตที่มีประสิทธิภาพมากกว่าทางด้านขวา นั่นคือ 1 = 1, x0 = 01 = 2, 1+x0 = 11 = 3, 1+x0+x2 = 11001000 = 19 และอื่นๆ ในการเป็นตัวแทนนี้ นั่นคือ 61779

การบวกในฟิลด์ไบนารีเป็นเพียง XOR (และการลบก็เช่นกัน) โปรดทราบว่านี่หมายถึง x+x = 0 สำหรับ x ใดๆ ในการคูณสององค์ประกอบ x*y เข้าด้วยกัน มีอัลกอริธึมการเรียกซ้ำที่ง่ายมาก: แบ่งแต่ละตัวเลขออกครึ่งหนึ่ง:

จากนั้นแยกการคูณ:

ส่วนสุดท้ายเป็นส่วนเดียวที่ยุ่งยากเล็กน้อย เนื่องจากคุณต้องใช้กฎการทำให้เข้าใจง่าย มีวิธีที่มีประสิทธิภาพมากกว่าในการคูณ คล้ายกับอัลกอริธึม Karatsubas และ Fast Fourier Transforms แต่ฉันจะปล่อยให้เป็นแบบฝึกหัดให้ผู้อ่านที่สนใจได้คิดออก

การหารในฟิลด์ไบนารีทำได้โดยการรวมการคูณและการผกผัน วิธีการผกผันแบบง่ายๆ แต่ช้าคือการประยุกต์ใช้ทฤษฎีบทเล็กของแฟร์แมตทั่วไป นอกจากนี้ยังมีอัลกอริธึมการผกผันที่ซับซ้อนกว่าแต่มีประสิทธิภาพมากกว่าซึ่งคุณสามารถพบได้ที่นี่ คุณสามารถใช้โค้ดที่นี่เพื่อเล่นกับการบวก การคูณ และการหารของเขตข้อมูลไบนารี่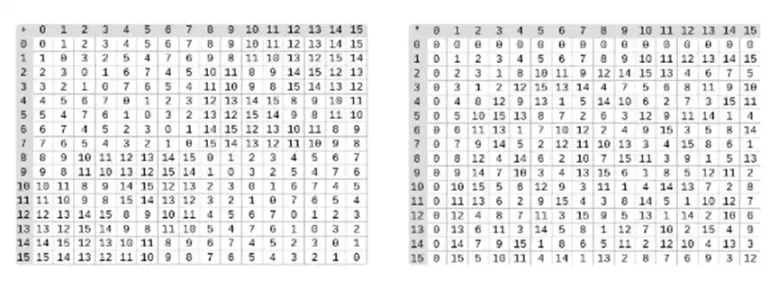

ซ้าย: ตารางเพิ่มเติมสำหรับองค์ประกอบฟิลด์ไบนารีสี่บิต (เช่น เพียง 1, x 0, x 1, x 0x 1) ขวา: ตารางสูตรคูณสำหรับองค์ประกอบฟิลด์ไบนารีสี่บิต

ความงดงามของสนามไบนารีประเภทนี้คือการที่รวมส่วนที่ดีที่สุดของจำนวนเต็มปกติและเลขคณิตแบบโมดูลาร์เข้าด้วยกัน เช่นเดียวกับจำนวนเต็มปกติ องค์ประกอบเขตข้อมูลไบนารี่ไม่มีขอบเขต คุณสามารถขยายให้ใหญ่ได้เท่าที่คุณต้องการ แต่เช่นเดียวกับเลขคณิตแบบโมดูลาร์ หากคุณดำเนินการกับค่าภายในขีดจำกัดขนาดหนึ่ง ผลลัพธ์ทั้งหมดของคุณจะยังคงอยู่ในช่วงเดียวกัน ตัวอย่างเช่น หากคุณนำ 42 ไปสู่พลังต่อเนื่อง คุณจะได้รับ:

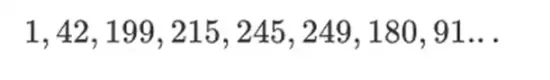
หลังจากผ่านไป 255 ก้าว คุณจะกลับมาที่ 42 ยกกำลัง 255 = 1 และเช่นเดียวกับจำนวนเต็มบวกและการดำเนินการแบบแยกส่วน พวกมันจะเป็นไปตามกฎทางคณิตศาสตร์ตามปกติ: a*b=b*a, a*(b+c)= a*b+a*c และแม้แต่กฎหมายใหม่ๆ แปลกๆ บ้าง

สุดท้ายนี้ เขตข้อมูลไบนารี่สะดวกสำหรับการจัดการบิต: ถ้าคุณคำนวณด้วยตัวเลขที่พอดีใน 2k ผลลัพธ์ทั้งหมดของคุณก็จะพอดีกับ 2,000 บิตเช่นกัน สิ่งนี้จะหลีกเลี่ยงความอึดอัดใจ ใน Ethereums EIP-4844 แต่ละบล็อกของ Blob ต้องเป็นตัวเลขแบบโมดูโล 52435875175126190479447740508185965837690552500527637822603658699938581184513 ดังนั้นการเข้ารหัสข้อมูลไบนารีจึงต้องทิ้งพื้นที่บางส่วนและทำการตรวจสอบเพิ่มเติมที่ ชั้นแอปพลิเคชันเพื่อให้แน่ใจว่าค่าที่เก็บไว้ในแต่ละองค์ประกอบจะน้อยกว่า 2248 นี้ ยังหมายความว่าการดำเนินการภาคสนามแบบไบนารีนั้นรวดเร็วเป็นพิเศษบนคอมพิวเตอร์ ทั้ง CPU และการออกแบบ FPGA และ ASIC ที่เหมาะสมตามหลักทฤษฎี

ทั้งหมดนี้หมายความว่าเราสามารถทำการเข้ารหัสรีด-โซโลมอนได้เหมือนที่เราทำข้างต้น ในลักษณะที่หลีกเลี่ยงการระเบิดจำนวนเต็มอย่างที่เราเห็นในตัวอย่างของเรา และด้วยวิธีการคำนวณแบบพื้นเมืองที่คอมพิวเตอร์ทำได้ดี คุณสมบัติการแยกของเขตข้อมูลไบนารี่ – วิธีที่เราสามารถทำได้ 1100101010001111 = 11001010 + 10001111*x 3 แล้วแยกออกตามที่เราต้องการ – ยังเป็นสิ่งสำคัญเพื่อให้มีความยืดหยุ่นอย่างมาก

ทำบิเนียสให้สมบูรณ์

ดู ที่นี่ สำหรับการนำโปรโตคอลไปใช้หลาม

ตอนนี้เราสามารถไปยัง "Binius แบบเต็ม" ซึ่งจะปรับ "Simple Binius" เป็น (i) ทำงานกับเขตข้อมูลไบนารี่และ (ii) ให้เราส่งบิตเดียว โปรโตคอลนี้เข้าใจยากเพราะมันสลับไปมาระหว่างวิธีการดูเมทริกซ์บิตที่แตกต่างกัน แน่นอนว่าฉันใช้เวลานานกว่าจะเข้าใจมากกว่าปกติในการเข้าใจโปรโตคอลการเข้ารหัส แต่เมื่อคุณเข้าใจเขตข้อมูลไบนารีแล้ว ข่าวดีก็คือว่า "คณิตศาสตร์ที่ยากกว่า" ที่ Binius อาศัยนั้นไม่มีอยู่จริง นี่ไม่ใช่การจับคู่เส้นโค้งรูปไข่ ซึ่งมีรูกระต่ายเรขาคณิตพีชคณิตที่ลึกลงไปอีกเรื่อยๆ ตรงนี้ คุณก็แค่มีเขตข้อมูลไบนารี่

มาดูแผนภูมิฉบับเต็มอีกครั้ง:

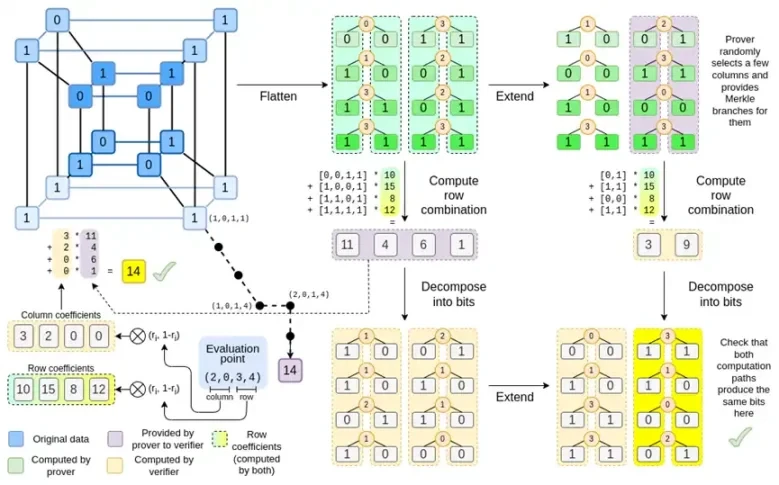
ถึงตอนนี้ คุณน่าจะคุ้นเคยกับส่วนประกอบส่วนใหญ่แล้ว แนวคิดในการทำให้ไฮเปอร์คิวบ์แบนราบเป็นตาราง แนวคิดในการคำนวณการรวมแถวและคอลัมน์เป็นผลคูณเทนเซอร์ของจุดประเมิน และแนวคิดในการตรวจสอบความเท่าเทียมกันระหว่างส่วนขยายรีด-โซโลมอน จากนั้นคำนวณการรวมแถวและการคำนวณการรวมแถว จากนั้นจึงคำนวณการขยายรีด-โซโลมอน ล้วนถูกนำไปใช้ใน Binius ธรรมดา

มีอะไรใหม่ใน Complete Binius? โดยพื้นฐานแล้วสามสิ่ง:

• แต่ละค่าในไฮเปอร์คิวบ์และสี่เหลี่ยมต้องเป็นบิต (0 หรือ 1)

• กระบวนการขยายจะขยายบิตออกเป็นบิตมากขึ้นโดยการจัดกลุ่มออกเป็นคอลัมน์และสมมติว่าเป็นองค์ประกอบของฟิลด์ที่ใหญ่กว่าชั่วคราว

• หลังจากขั้นตอนการรวมแถว จะมีการแบ่งแยกองค์ประกอบเป็นขั้นตอนบิตซึ่งจะแปลงการขยายกลับเป็นบิต

ค่อยหารือกันทั้งสองกรณีตามลำดับ ขั้นแรกให้ขยายขั้นตอนใหม่ รหัสรีด-โซโลมอนมีข้อจำกัดพื้นฐาน หากคุณต้องการขยาย n ถึง k*n คุณต้องทำงานในฟิลด์ที่มีค่าต่างกัน k*n ซึ่งสามารถใช้เป็นพิกัดได้ ด้วย F 2 (หรือที่เรียกว่าบิต) คุณไม่สามารถทำเช่นนั้นได้ สิ่งที่เราทำคือรวมองค์ประกอบที่อยู่ติดกันของ F 2 เข้าด้วยกันเพื่อสร้างค่าที่มากขึ้น ในตัวอย่างนี้ เราบรรจุครั้งละสองบิตลงในองค์ประกอบ { 0 , 1 , 2 , 3 } ซึ่งเพียงพอสำหรับเราเนื่องจากส่วนขยายของเรามีจุดคำนวณเพียงสี่จุดเท่านั้น ในการพิสูจน์จริง เราอาจย้อนกลับไปครั้งละ 16 บิต จากนั้นเราจะรันโค้ด Reed-Solomon กับค่าที่แพ็กเหล่านี้ และแตกแพ็กออกเป็นบิตอีกครั้ง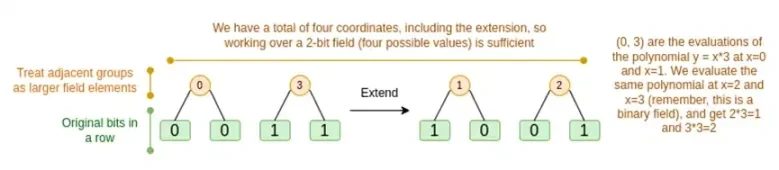

ตอนนี้การรวมแถว เพื่อให้การประเมินที่การตรวจสอบจุดสุ่มมีความปลอดภัยแบบเข้ารหัส เราจำเป็นต้องสุ่มตัวอย่างจุดนั้นจากพื้นที่ที่ค่อนข้างใหญ่ (ใหญ่กว่าไฮเปอร์คิวบ์มาก) ดังนั้นแม้ว่าจุดภายในไฮเปอร์คิวบ์จะเป็นบิต แต่ค่าที่คำนวณได้ภายนอกไฮเปอร์คิวบ์จะมีค่ามากกว่ามาก ในตัวอย่างข้างต้น ชุดค่าผสมของแถวจะกลายเป็น [11, 4, 6, 1]

สิ่งนี้ทำให้เกิดปัญหา: เรารู้วิธีจัดกลุ่มบิตให้เป็นค่าที่มากขึ้น จากนั้นจึงทำการขยาย Reed-Solomon กับค่านั้น แต่เราจะทำสิ่งเดียวกันสำหรับคู่ค่าที่ใหญ่กว่าได้อย่างไร

เคล็ดลับของ Binius คือการทำมันทีละนิด: เราดูทีละบิตของแต่ละค่า (เช่น สำหรับสิ่งที่เราเรียกว่า 11 นั่นคือ [1, 1, 0, 1]) จากนั้นเราจะขยายมันทีละแถว นั่นคือเราขยายมันไปที่ 1 แถวของแต่ละองค์ประกอบ จากนั้นในแถว x0 จากนั้นในแถว x1 จากนั้นในแถว x0x1 และอื่น ๆ (ในตัวอย่างของเล่นของเรา เราหยุดอยู่แค่นั้น แต่ในความเป็นจริง นำไปปฏิบัติสูงสุด 128 แถว (อันสุดท้ายคือ x6*…*x0))

ทบทวน:

• เราแปลงบิตในไฮเปอร์คิวบ์ให้เป็นตาราง

• จากนั้นเราจะถือว่ากลุ่มของบิตที่อยู่ติดกันในแต่ละแถวเป็นองค์ประกอบของฟิลด์ที่ใหญ่กว่า และดำเนินการทางคณิตศาสตร์กับบิตเหล่านั้นเพื่อให้รีด-โซโลมอนขยายแถว

• จากนั้นเราจะนำการรวมแถวของแต่ละคอลัมน์ของบิตและรับคอลัมน์ของบิตสำหรับแต่ละแถวเป็นเอาต์พุต (เล็กกว่ามากสำหรับสี่เหลี่ยมที่มีขนาดใหญ่กว่า 4 x 4)

• จากนั้นเราพิจารณาเอาต์พุตเป็นเมทริกซ์และบิตของมันคือแถว

ทำไมสิ่งนี้ถึงเกิดขึ้น? ในคณิตศาสตร์ปกติ หากคุณเริ่มหั่นตัวเลขทีละนิด ความสามารถ (ปกติ) ในการดำเนินการเชิงเส้นในลำดับใดๆ ก็ได้และได้ผลลัพธ์เดียวกันจะพังทลายลง ตัวอย่างเช่น ถ้าฉันเริ่มต้นด้วยตัวเลข 345 และคูณด้วย 8 แล้วด้วย 3 ฉันจะได้ 8280 และถ้าฉันดำเนินการทั้งสองแบบย้อนกลับ ฉันจะได้ 8280 ด้วย แต่ถ้าฉันแทรกการดำเนินการแบ่งส่วนบิต ระหว่างสองขั้นตอน จะแบ่งย่อย: ถ้าคุณทำ 8x แล้วก็ 3x คุณจะได้รับ: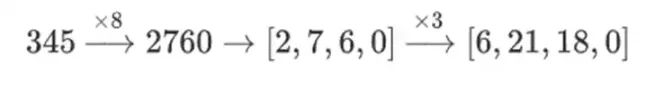

แต่ถ้าคุณทำ 3x แล้วก็ 8x คุณจะได้:

แต่ในสนามไบนารี่ที่สร้างด้วยโครงสร้างหอคอย วิธีนี้ใช้ได้ผล เหตุผลก็คือแยกกันไม่ได้: หากคุณคูณค่ามากด้วยค่าน้อย สิ่งที่เกิดขึ้นในแต่ละเซ็กเมนต์จะยังคงอยู่ในแต่ละเซ็กเมนต์ ถ้าเราคูณ 1100101010001111 ด้วย 11 ก็จะเหมือนกับการสลายตัวครั้งแรกของ 1100101010001111 ซึ่งก็คือ

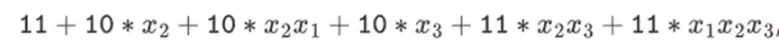
จากนั้นคูณแต่ละองค์ประกอบด้วย 11

วางมันทั้งหมดเข้าด้วยกัน

โดยทั่วไป ระบบพิสูจน์ความรู้เป็นศูนย์ทำงานโดยสร้างข้อความเกี่ยวกับพหุนามที่แสดงถึงข้อความเกี่ยวกับการประเมินที่สำคัญในเวลาเดียวกัน: เช่นเดียวกับที่เราเห็นในตัวอย่างฟีโบนักชี F(X+ 2)-F(X+ 1)-F( X) = Z(X)*H(X) ในขณะที่ตรวจสอบทุกขั้นตอนของการคำนวณ Fibonacci เราตรวจสอบข้อความเกี่ยวกับพหุนามโดยการพิสูจน์การประเมินที่จุดสุ่ม การตรวจสอบจุดสุ่มนี้แสดงถึงการตรวจสอบพหุนามทั้งหมด หากสมการพหุนามไม่ตรงกัน ก็มีโอกาสเล็กน้อยที่สมการจะตรงกันที่พิกัดสุ่มเฉพาะ

ในทางปฏิบัติ สาเหตุหลักประการหนึ่งของความไร้ประสิทธิภาพคือในโปรแกรมจริง ตัวเลขส่วนใหญ่ที่เราจัดการมีขนาดเล็ก เช่น ดัชนีใน for loops ค่า True/False ตัวนับ และอะไรทำนองนั้น อย่างไรก็ตาม เมื่อเราขยายข้อมูลด้วยการเข้ารหัส Reed-Solomon เพื่อให้เกิดความซ้ำซ้อนที่จำเป็นในการทำให้การตรวจสอบแบบ Merkle-proof มีความปลอดภัย ค่าพิเศษส่วนใหญ่จะกินพื้นที่ทั้งขนาดฟิลด์ แม้ว่าค่าเดิมจะน้อยก็ตาม

เพื่อแก้ไขปัญหานี้ เราต้องการทำให้ฟิลด์นี้มีขนาดเล็กที่สุดเท่าที่จะเป็นไปได้ Plonky 2 นำเราจากตัวเลข 256 บิตไปเป็นตัวเลข 64 บิต จากนั้น Plonky 3 ก็ลดลงเหลือ 31 บิต แต่นั่นก็ยังไม่เหมาะสมที่สุด ด้วยฟิลด์ไบนารี เราสามารถจัดการกับบิตเดี่ยวได้ สิ่งนี้ทำให้การเข้ารหัสหนาแน่น: หากข้อมูลที่แท้จริงของคุณมี n บิต การเข้ารหัสของคุณก็จะมี n บิต และส่วนขยายจะมี 8*n บิต โดยไม่มีค่าใช้จ่ายเพิ่มเติม

ตอนนี้เรามาดูแผนภูมินี้เป็นครั้งที่สาม:

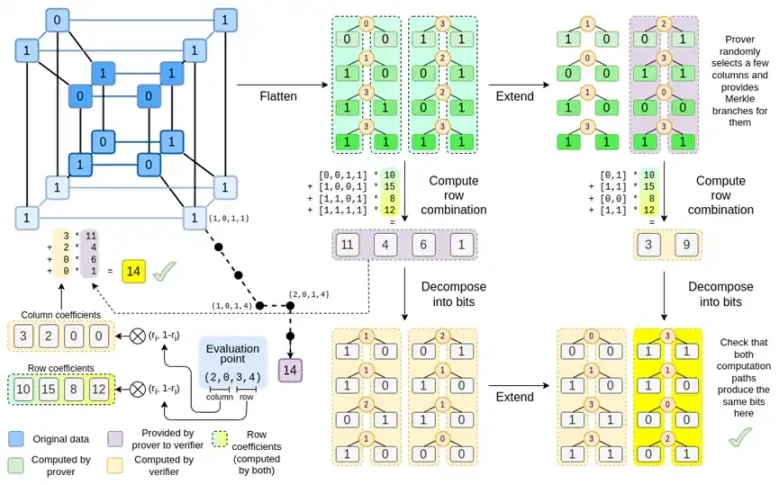
ใน Binius เราทำงานกับพหุนามหลายเส้น: ไฮเปอร์คิวบ์ P(x0, x1,…xk) โดยที่การประเมินเดี่ยว P(0, 0, 0, 0), P(0, 0, 0, 1) จนถึง P( 1, 1, 1, 1) เก็บข้อมูลที่เราสนใจ เพื่อพิสูจน์การคำนวณ ณ จุดใดจุดหนึ่ง เราจะตีความข้อมูลเดียวกันใหม่เป็นสี่เหลี่ยมจัตุรัส จากนั้นเราจะขยายแต่ละแถวโดยใช้การเข้ารหัส Reed-Solomon เพื่อให้ข้อมูลซ้ำซ้อนที่จำเป็นสำหรับการรักษาความปลอดภัยจากการสืบค้นสาขา Merkle แบบสุ่ม จากนั้นเราจะคำนวณผลรวมเชิงเส้นแบบสุ่มของแถว โดยออกแบบค่าสัมประสิทธิ์เพื่อให้แถวที่รวมใหม่มีค่าที่คำนวณได้ที่เราสนใจจริงๆ แถวที่สร้างขึ้นใหม่นี้ (ตีความใหม่เป็นแถว 128 บิต) และคอลัมน์ที่เลือกแบบสุ่มบางส่วนที่มีกิ่งก้านของ Merkle จะถูกส่งผ่านไปยังตัวตรวจสอบ

จากนั้นตัวตรวจสอบจะดำเนินการรวมแถวที่ขยาย (หรือเจาะจงกว่านั้นคือคอลัมน์ที่ขยาย) และการรวมแถวที่ขยาย และตรวจสอบว่าทั้งสองตรงกัน จากนั้นจะคำนวณการรวมคอลัมน์และตรวจสอบว่าส่งคืนค่าที่ผู้พิสูจน์อ้างสิทธิ์หรือไม่ นี่คือระบบการพิสูจน์ของเรา (หรือถ้าให้เจาะจงกว่านั้นคือ โครงการข้อผูกมัดพหุนาม ซึ่งเป็นองค์ประกอบสำคัญของระบบการพิสูจน์)

สิ่งที่เรายังไม่ได้ครอบคลุมยัง?

• จำเป็นต้องมีอัลกอริธึมที่มีประสิทธิภาพในการขยายแถวเพื่อทำให้เครื่องมือตรวจสอบความถูกต้องมีประสิทธิภาพในการคำนวณ เราใช้การแปลงฟูเรียร์แบบรวดเร็วบนฟิลด์ไบนารี ตามที่อธิบายไว้ที่นี่ (แม้ว่าการใช้งานจริงจะแตกต่างออกไป เนื่องจากโพสต์นี้ใช้โครงสร้างที่มีประสิทธิภาพน้อยกว่าซึ่งไม่ได้ขึ้นอยู่กับการขยายแบบเรียกซ้ำ)

• ในทางคณิตศาสตร์ พหุนามตัวแปรเดียวนั้นสะดวกเพราะคุณสามารถทำสิ่งต่างๆ เช่น F(X+2)-F(X+1)-F(X) = Z(X)*H(X) เพื่อเชื่อมโยงขั้นตอนที่อยู่ติดกันในการคำนวณ ในไฮเปอร์คิวบ์ ขั้นตอนถัดไปอธิบายได้น้อยกว่า X+1 มาก คุณสามารถทำ X+k พลังของ k ได้ แต่พฤติกรรมการกระโดดนี้ทำให้ข้อดีที่สำคัญของ Binius หลายประการลดลง เอกสาร Binius อธิบายวิธีแก้ปัญหา ดูหัวข้อ 4.3) แต่นี่เป็นรูกระต่ายที่ลึกในตัวเอง

• วิธีตรวจสอบค่าเฉพาะอย่างปลอดภัย ตัวอย่าง Fibonacci จำเป็นต้องตรวจสอบเงื่อนไขขอบเขตที่สำคัญ: ค่าของ F(0)=F(1)=1 และ F(100) แต่สำหรับ Binius ดั้งเดิม การตรวจสอบ ณ จุดคำนวณที่ทราบนั้นไม่ปลอดภัย มีวิธีที่ค่อนข้างง่ายในการแปลงการตรวจสอบการคำนวณที่ทราบไปเป็นการตรวจสอบการคำนวณที่ไม่รู้จัก โดยใช้สิ่งที่เรียกว่าโปรโตคอลการตรวจสอบผลรวม แต่เราจะไม่ครอบคลุมสิ่งเหล่านั้นที่นี่

• โปรโตคอลการค้นหาซึ่งเป็นอีกเทคโนโลยีหนึ่งที่ใช้กันอย่างแพร่หลายเมื่อเร็ว ๆ นี้ ถูกนำมาใช้เพื่อสร้างระบบพิสูจน์อักษรที่มีประสิทธิภาพสูง Binius สามารถใช้ร่วมกับโปรโตคอลการค้นหาสำหรับแอปพลิเคชันจำนวนมาก

• เกินเวลาการตรวจสอบรากที่สอง รากที่สองมีราคาแพง: การพิสูจน์ Binius ขนาด 2^32 บิตจะมีความยาวประมาณ 11 MB คุณสามารถชดเชยสิ่งนี้ได้โดยใช้ระบบพิสูจน์อื่นๆ เพื่อสร้างข้อพิสูจน์ของการพิสูจน์ Binius ซึ่งจะทำให้คุณได้รับประสิทธิภาพของการพิสูจน์ Binius ด้วยขนาดการพิสูจน์ที่เล็กลง อีกทางเลือกหนึ่งคือโปรโตคอล FRI-Binius ที่ซับซ้อนกว่า ซึ่งสร้างการพิสูจน์ขนาดหลายลอการิทึม (เช่นเดียวกับ FRI ทั่วไป)

• Binius ส่งผลต่อความเป็นมิตรต่อ SNARK อย่างไร บทสรุปพื้นฐานคือ หากคุณใช้ Binius คุณไม่จำเป็นต้องใส่ใจกับการคำนวณที่เป็นมิตรต่อการคำนวณอีกต่อไป การแฮชแบบปกติจะไม่มีประสิทธิภาพมากกว่าการแฮชทางคณิตศาสตร์แบบดั้งเดิมอีกต่อไป การคูณโมดูโล 2 ยกกำลัง 32 หรือโมดูโล 2 ยกกำลัง 256 จะไม่เจ็บปวดเท่ากับการคูณโมดูโล 2 อีกต่อไป ฯลฯ แต่นี่เป็นหัวข้อที่ซับซ้อน มีหลายสิ่งหลายอย่างเปลี่ยนไปเมื่อทุกอย่างเสร็จสิ้นในรูปแบบไบนารี

ฉันคาดว่าจะเห็นการปรับปรุงเพิ่มเติมในเทคโนโลยีการพิสูจน์ภาคสนามแบบไบนารีในอีกไม่กี่เดือนข้างหน้า

บทความนี้มาจากอินเทอร์เน็ต: Vitalik: Binius การพิสูจน์ที่มีประสิทธิภาพสำหรับเขตข้อมูลไบนารี

ที่เกี่ยวข้อง: เหรียญ BNB แสดงสัญญาณการฟื้นตัว: จุดสูงสุดใหม่ประจำปีที่เห็น

โดยสรุป ราคา BNB ดีดตัวกลับจาก $550 เข้าใกล้แนวต้าน $593 อีกนิ้ว ตัวชี้วัดราคาฟื้นโมเมนตัมขาขึ้น ซึ่งสนับสนุนการเพิ่มขึ้น 8% Sharpe Ratio ที่ 4.03 มีแนวโน้มที่จะผลักดันนักลงทุนรายใหม่ให้หันมาใช้โทเค็นการแลกเปลี่ยน เดือนมีนาคมเป็นเดือนที่ดีสำหรับ BNB Coin โดยสกุลเงินดิจิทัลบรรลุจุดสูงสุดใหม่สองครั้งในรอบปีภายในเพียงไม่กี่วันก่อนที่จะมีการปรับฐาน หลังจากการฟื้นตัวเกือบสองสัปดาห์ BNB Coin กำลังแสดงสัญญาณที่อาจถึงระดับสูงสุดใหม่ในปี 2024 แต่เหตุการณ์สำคัญดังกล่าวจะเกิดขึ้นได้หรือไม่ BNB ดูมีแนวโน้มดี หลังจากการดีดตัวจากระดับแนวรับ $550 มูลค่าของ BNB Coin ได้เพิ่มขึ้นเป็น $581 ในขณะที่ทำการวิเคราะห์นี้ การปรับปรุงนี้สะท้อนให้เห็นถึงการฟื้นตัวของโปรไฟล์ผลตอบแทนความเสี่ยงของ altcoin...