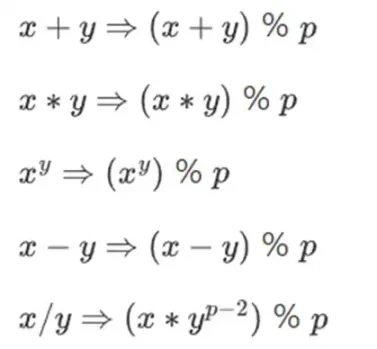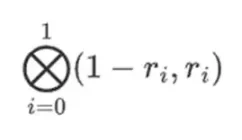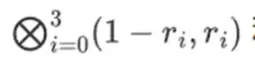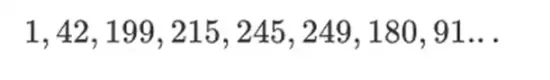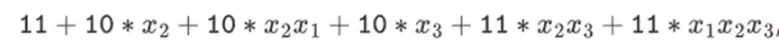Виталик: Биниус, эффективные доказательства для бинарных полей

Оригинал статьи: Виталик Бутерин

Оригинальный перевод: Кейт, MarsBit

Этот пост предназначен в первую очередь для читателей, которые в целом знакомы с криптографией эпохи 2019 года, в частности с SNARK и STARK. Если нет, то я рекомендую сначала прочитать их. Особая благодарность Джастину Дрейку, Джиму Позену, Бенджамину Даймонду и Ради Койбашичу за их отзывы и комментарии.

За последние два года STARK стали ключевой и незаменимой технологией для эффективного создания легко проверяемых криптографических доказательств очень сложных утверждений (например, доказательство того, что блок Ethereum является действительным). Одной из основных причин этого является небольшой размер поля: SNARK, основанные на эллиптических кривых, требуют, чтобы вы работали с 256-битными целыми числами, чтобы быть достаточно безопасными, в то время как STARK позволяют вам использовать гораздо меньшие размеры полей с большей эффективностью: сначала поле Goldilocks (64-битное целое число), затем Mersenne 31 и BabyBear (оба по 31 бит). Благодаря этим повышениям эффективности Plonky 2, использующий Goldilocks, в сотни раз быстрее своих предшественников при доказательстве многих видов вычислений.

Естественный вопрос: можем ли мы довести эту тенденцию до логического завершения и построить системы доказательства, которые будут работать быстрее, оперируя непосредственно нулями и единицами? Это именно то, что пытается сделать Биниус, используя ряд математических уловок, которые сильно отличают его от SNARK и STARK трехлетней давности. В этом посте описывается, почему небольшие поля делают генерацию доказательств более эффективными, почему бинарные поля обладают уникальной мощью, а также приемы, которые использует Биниус, чтобы сделать доказательства для бинарных полей такими эффективными.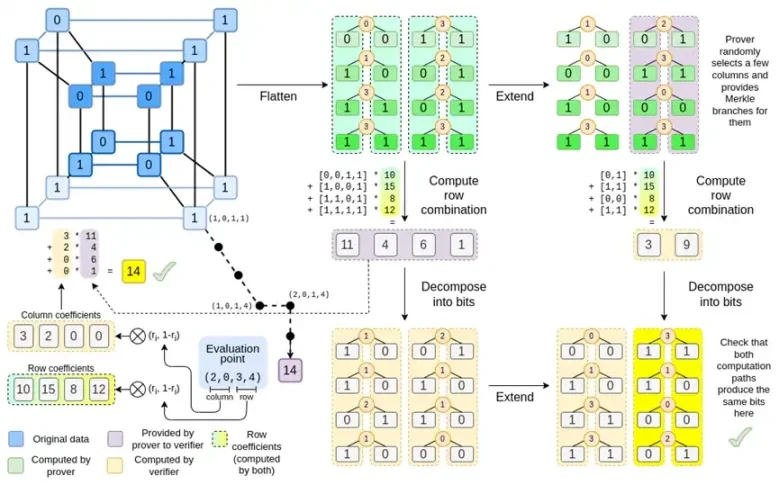

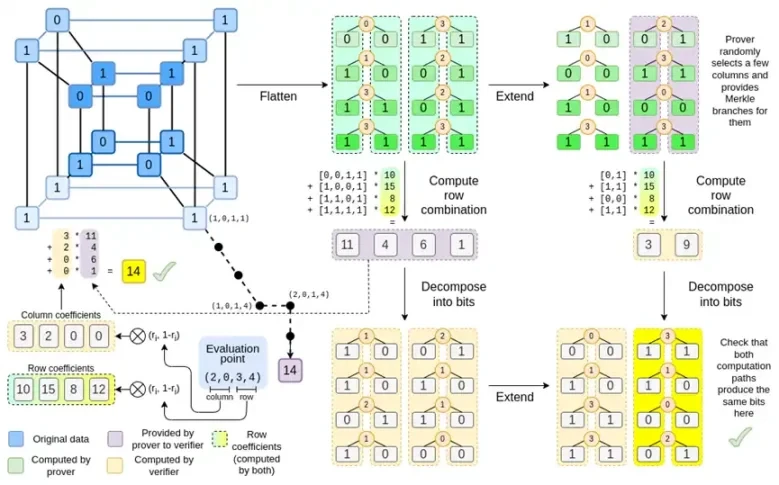
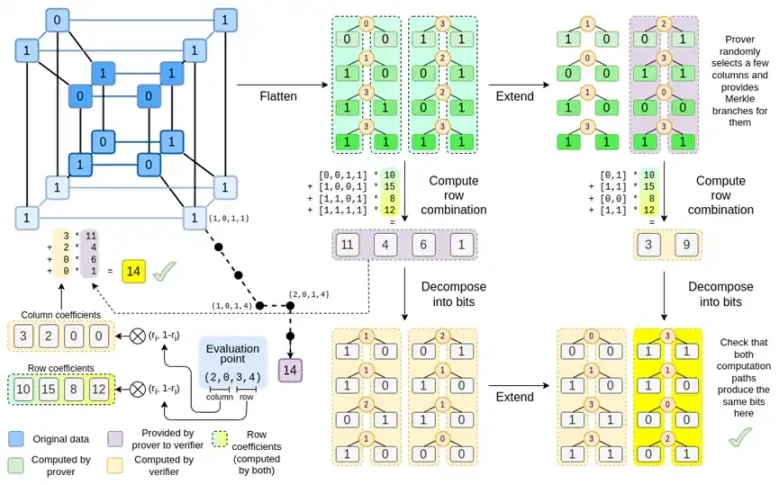
Биниус, к концу этого поста вы сможете понять каждую часть этой диаграммы.

Обзор: конечные поля

Одна из ключевых задач систем криптографических доказательств — работать с большими объемами данных, сохраняя их небольшими. Если вы сможете сжать утверждение о большой программе в математическое уравнение, содержащее несколько чисел, но эти числа будут такими же большими, как исходная программа, то вы ничего не получите.

Чтобы выполнять сложную арифметику, сохраняя при этом небольшие числа, криптографы часто используют модульную арифметику. Выбираем модуль простого числа p. Оператор % означает получение остатка: 15% 7 = 1, 53% 10 = 3 и так далее. (Обратите внимание, что ответ всегда неотрицательный, например -1% 10 = 9)

Возможно, вы видели модульную арифметику в контексте сложения и вычитания времени (например, сколько сейчас времени через 4 часа после 9?). Но здесь мы не просто складываем и вычитаем число по модулю; мы также можем умножать, делить и брать показатели.

Мы переопределяем:

Все вышеперечисленные правила являются самосогласованными. Например, если p = 7, то:

5 + 3 = 1 (потому что 8% 7 = 1)

1-3 = 5 (потому что -2% 7 = 5)

2* 5 = 3

3/5 = 2

Более общий термин для таких структур — конечные поля. Конечное поле — это математическая структура, которая следует обычным законам арифметики, но в которой число возможных значений конечно, так что каждое значение может быть представлено фиксированным размером.

Модульная арифметика (или простые поля) — наиболее распространенный тип конечных полей, но есть и другой тип: поля расширения. Возможно, вы видели одно поле расширения: комплексные числа. Мы представляем новый элемент, обозначаем его i и выполняем с ним математические операции: (3i+2)*(2i+4)=6i*i+12i+4i+8=16i+2. Мы можем сделать то же самое с расширением простого поля. Когда мы начинаем иметь дело с меньшими полями, расширение простых полей становится все более важным для безопасности, а двоичные поля (используемые Биниусом) полностью полагаются на расширение, чтобы иметь практическую полезность.

Обзор: Арифметизация

Методы SNARK и STARK доказывают компьютерные программы с помощью арифметики: вы берете утверждение о программе, которую хотите доказать, и превращаете его в математическое уравнение, включающее полином. Правильное решение уравнения соответствует правильному выполнению программы.

В качестве простого примера предположим, что я вычислил сотое число Фибоначчи и хочу доказать вам, что это такое. Я создаю полином F, который кодирует последовательность Фибоначчи: поэтому F(0)=F(1)=1, F(2)=2, F(3)=3, F(4)=5 и так далее в течение 100 шагов. . Условие, которое мне нужно доказать, заключается в том, что F(x+2)=F(x)+F(x+1) во всем диапазоне x={0, 1…98}. Я могу убедить вас, указав частное:

где Z(x) = (x-0) * (x-1) * …(x-98). . Если я могу обеспечить, чтобы F и H удовлетворяли этому уравнению, тогда F должно удовлетворять F(x+2)-F(x+1)-F(x) в диапазоне. Если я дополнительно проверю, что для F F(0)=F(1)=1, то F(100) на самом деле должно быть 100-м числом Фибоначчи.

Если вы хотите доказать что-то более сложное, то вы заменяете простое соотношение F(x+2) = F(x) + F(x+1) более сложным уравнением, которое по сути утверждает, что F(x+1) — это результат. инициализации виртуальной машины с состоянием F(x) и выполнения одного вычислительного шага. Вы также можете заменить число 100 на большее число, например, 100000000, чтобы вместить больше шагов.

Все SNARK и STARK основаны на идее использования простых уравнений над полиномами (а иногда и векторами и матрицами) для представления большого количества связей между отдельными значениями. Не все алгоритмы проверяют эквивалентность между соседними вычислительными шагами, как указано выше: например, PLONK этого не делает, равно как и R1CS. Но многие из наиболее эффективных проверок так и делают, потому что легче минимизировать накладные расходы, выполняя одну и ту же проверку (или несколько одних и тех же проверок) много раз.

Plonky 2: От 256-битных SNARK и STARK к 64-битным… только STARK

Пять лет назад разумное изложение различных типов доказательств с нулевым разглашением было следующим. Существует два типа доказательств: SNARK (на основе эллиптических кривых) и STARK (на основе хеша). Технически STARK — это разновидность SNARK, но на практике обычно используется «SNARK» для обозначения варианта на основе эллиптической кривой, а «STARK» — для обозначения конструкции на основе хеш-функции. SNARK небольшие, поэтому вы можете очень быстро их проверить и легко установить в цепочку. STARK большие, но они не требуют надежной настройки и квантово-устойчивы.

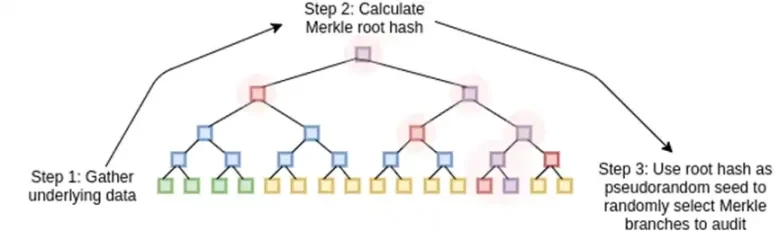
STARK работают, рассматривая данные как полином, вычисляя вычисление этого полинома и используя корень Меркла расширенных данных как «полиномиальное обязательство».

Ключевым моментом истории здесь является то, что сначала широко использовались SNARK на основе эллиптических кривых: STARK не стали достаточно эффективными примерно до 2018 года, благодаря FRI, а к тому времени Zcash работал уже больше года. SNARK на основе эллиптической кривой имеет ключевое ограничение: если вы хотите использовать SNARK на основе эллиптической кривой, то арифметика в этих уравнениях должна выполняться по модулю количества точек на эллиптической кривой. Это большое число, обычно близкое к 2 в степени 256: например, для кривой bn128 это 21888242871839275222246405745257275088548364400416034343698204186575808495617. Но в реальных вычислениях используются небольшие числа: если подумать о реальной программе на вашем любимом языке, большая часть ее используются счетчики, индексы в циклах for, позиции в программе, отдельные биты, представляющие истину или ложь, и другие вещи, длина которых почти всегда составляет всего несколько цифр.

Даже если ваши исходные данные состоят из небольших чисел, процесс доказательства требует вычисления коэффициентов, разложений, случайных линейных комбинаций и других преобразований данных, которые приведут к получению равного или большего количества объектов, размер которых в среднем равен полному размеру вашего файла. поле. Это создает ключевую неэффективность: чтобы доказать вычисление на n малых значениях, вам нужно выполнить гораздо больше вычислений на n гораздо больших значениях. Первоначально STARK унаследовали привычку SNARK использовать 256-битные поля и, таким образом, страдали от той же неэффективности.

Разложение Рида-Соломона некоторой полиномиальной оценки. Несмотря на то, что исходное значение небольшое, дополнительные значения расширяются до полного размера поля (в данном случае 2^31 – 1).

В 2022 году вышел Plonky 2. Основное нововведение Plonky 2 — выполнение арифметических операций по модулю меньшего простого числа: 2 в 64-й степени — 2 в 32-й степени + 1 = 18446744067414584321. Теперь каждое сложение или умножение всегда можно выполнить с помощью нескольких инструкций на компьютере. ЦП, а хеширование всех данных происходит в 4 раза быстрее, чем раньше. Но есть проблема: этот метод работает только для STARK. Если вы попытаетесь использовать SNARK, эллиптические кривые станут небезопасными для таких маленьких эллиптических кривых.

Для обеспечения безопасности Plonky 2 также необходимо ввести поля расширения. Ключевым методом проверки арифметических уравнений является выборка случайных точек: если вы хотите проверить, равно ли H(x) * Z(x) F(x+2)-F(x+1)-F(x), вы можете случайным образом выберите координату r, обеспечьте полиномиальное обязательство, чтобы доказать H(r), Z(r), F(r), F(r+1) и F(r+2), а затем проверьте, соответствует ли H(r) * Z(r ) равно F(r+2)-F(r+1)-F(r). Если злоумышленник сможет заранее угадать координаты, то злоумышленник может обмануть систему доказательств – именно поэтому система доказательств должна быть случайной. Но это также означает, что координаты должны быть выбраны из достаточно большого набора, чтобы злоумышленник не мог угадать их случайным образом. Это, очевидно, верно, если модуль близок к 2 в степени 256. Однако для модуля 2^64 – 2^32 + 1 мы еще не достигли цели, и это определенно не тот случай, если мы приступим к 2^31 – 1. Злоумышленнику вполне по силам попытаться подделать доказательство два миллиарда раз, пока одному не повезет.

Чтобы предотвратить это, мы выбираем r из расширенного поля, чтобы, например, можно было определить y, где y^3 = 5, и взять комбинации 1, y и y^2. Это доводит общее количество координат примерно до 2^93. Большинство полиномов, вычисленных средством доказателя, не попадают в это расширенное поле; это просто целые числа по модулю 2^31-1, так что вы все равно получите всю эффективность от использования небольшого поля. Но выборочные проверки точек и вычисления FRI действительно затрагивают эту более широкую область, чтобы обеспечить необходимую им безопасность.

От маленьких простых чисел к двоичным числам

Компьютеры выполняют арифметические действия, представляя большие числа в виде последовательностей нулей и единиц и создавая схемы поверх этих битов для вычисления таких операций, как сложение и умножение. Компьютеры особенно оптимизированы для 16-, 32- и 64-битных целых чисел. Например, 2^64 – 2^32 + 1 и 2^31 – 1 были выбраны не только потому, что они укладываются в эти границы, но и потому, что они хорошо вписываются в эти границы: умножение по модулю 2^64 – 2^32 + 1. может быть выполнено путем обычного 32-битного умножения, побитового сдвига и копирования вывода в нескольких местах; эта статья хорошо объясняет некоторые трюки.

Однако гораздо лучшим подходом было бы выполнять вычисления непосредственно в двоичном формате. Что, если бы сложение могло быть простым исключающим ИЛИ, без необходимости беспокоиться о переносе при сложении 1 + 1 из одного бита в другой? Что, если бы умножение можно было бы более распараллелить таким же образом? Все эти преимущества основаны на возможности представления значений true/false с помощью одного бита.

Получение этих преимуществ непосредственного выполнения двоичных вычислений — это именно то, что пытается сделать Binius. Команда Binius продемонстрировала повышение эффективности в своей презентации на zkSummit:

Несмотря на примерно одинаковый размер, операции с 32-битными двоичными полями требуют в 5 раз меньше вычислительных ресурсов, чем операции с 31-битными полями Мерсенна.

От одномерных полиномов к гиперкубам

Предположим, мы верим этому рассуждению и хотим делать все с битами (0 и 1). Как мы можем представить миллиард битов одним полиномом?

Здесь мы сталкиваемся с двумя практическими проблемами:

1. Чтобы полином представлял большое количество значений, эти значения должны быть доступны при вычислении полинома: в приведенном выше примере Фибоначчи F(0), F(1)… F(100), а в более крупном вычислении , показатели будут исчисляться миллионами. Поля, которые мы используем, должны содержать числа такого размера.

2. Доказательство любого значения, которое мы фиксируем в дереве Меркла (как и все STARK), требует его кодирования Рида-Соломона: например, расширения значений от n до 8n, использования избыточности, чтобы предотвратить мошенничество злоумышленников путем подделки значения во время расчета. Для этого также требуется наличие достаточно большого поля: чтобы расширить число значений с миллиона до 8 миллионов, вам потребуется 8 миллионов различных точек для оценки полинома.

Ключевая идея Binius состоит в том, чтобы решить эти две проблемы по отдельности, представляя одни и те же данные двумя разными способами. Во-первых, сами полиномы. Такие системы, как SNARK на основе эллиптических кривых, STARK 2019 года, Plonky 2 и другие, обычно имеют дело с полиномами от одной переменной: F(x). Биниус, с другой стороны, черпает вдохновение из спартанского протокола и использует многомерные полиномы: F(x 1, x 2,… xk). По сути, мы представляем всю вычислительную траекторию в гиперкубе вычислений, где каждый xi равен либо 0, либо 1. Например, если мы хотим представить последовательность Фибоначчи и по-прежнему используем поле, достаточно большое для их представления, мы можем представьте себе их первые 16 последовательностей так:

То есть F(0,0,0,0) должно быть 1, F(1,0,0,0) тоже 1, F(0,1,0,0) равно 2 и так далее, все вплоть до F(1,1,1,1) = 987. Учитывая такой гиперкуб вычислений, существует многомерный линейный (степень 1 по каждой переменной) многочлен, который производит эти вычисления. Таким образом, мы можем думать об этом наборе значений как о представлении полинома; нам не нужно вычислять коэффициенты.

Этот пример, конечно, просто для иллюстрации: на практике весь смысл изучения гиперкуба состоит в том, чтобы позволить нам иметь дело с отдельными битами. Родной для Binius способ вычисления чисел Фибоначчи заключается в использовании многомерного куба, хранящего одно число в каждой группе, скажем, из 16 бит. Это требует некоторой смекалки для реализации сложения целых чисел на битовой основе, но для Binius это не слишком сложно.

Теперь давайте посмотрим на коды стирания. Принцип работы STARK заключается в том, что вы берете n значений, Рид-Соломон расширяет их до большего количества значений (обычно 8n, обычно между 2n и 32n), затем случайным образом выбираете некоторые ветви Меркла из расширения и выполняете над ними какую-то проверку. Гиперкуб имеет длину 2 в каждом измерении. Поэтому расширять его напрямую нецелесообразно: недостаточно места для выборки ветвей Меркла из 16 значений. Так как же нам это сделать? Предположим, гиперкуб представляет собой квадрат!

Простой Биниус – пример

Видеть здесь для реализации протокола на Python.

Давайте рассмотрим пример, в котором для удобства в качестве полей используются обычные целые числа (в реальной реализации мы бы использовали элементы двоичных полей). Сначала мы кодируем гиперкуб, который хотим представить, как квадрат:

Теперь расширим квадрат, используя метод Рида-Соломона. То есть мы рассматриваем каждую строку как полином степени 3, оцененный в точке x = { 0, 1, 2, 3 }, и оцениваем тот же полином в точке x = { 4, 5, 6, 7 }: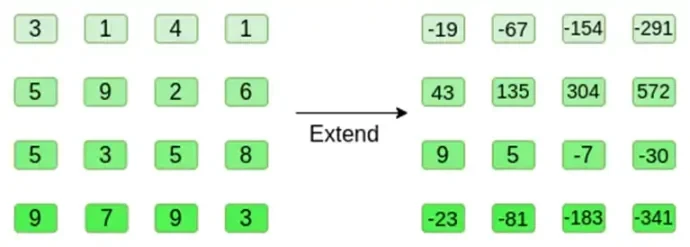

Обратите внимание, что цифры могут быть очень большими! Вот почему в практических реализациях мы всегда используем конечные поля, а не обычные целые числа: например, если мы используем целые числа по модулю 11, расширение первой строки будет просто [3, 10, 0, 6].

Если вы хотите опробовать расширение и проверить номера самостоятельно, вы можете использовать мой простой код расширения Рида-Соломона здесь.

Далее мы рассматриваем это расширение как столбец и создаем дерево Меркла для столбца. Корень дерева Меркла – это наша приверженность.

Теперь предположим, что доказывающая хочет доказать вычисление этого многочлена r = {r 0, r 1, r 2, r 3 } в какой-то момент. В Биниусе есть тонкое отличие, которое делает его более слабым по сравнению с другими схемами полиномиального обязательства: доказывающий не должен знать или быть в состоянии угадать s до перехода к корню Меркла (другими словами, r должно быть псевдослучайным значением, которое зависит от корень Меркла). Это делает схему бесполезной для поиска в базе данных (например, вы дали мне корень Меркла, теперь докажите мне P(0, 0, 1, 0)!). Но протоколы доказательства с нулевым разглашением, которые мы на самом деле используем, обычно не требуют поиска в базе данных; они требуют только проверки полинома в случайной точке оценки. Так что это ограничение хорошо служит нашим целям.

Предположим, мы выбираем r = { 1, 2, 3, 4 } (многочлен оценивается как -137; вы можете подтвердить это с помощью этого кода). Теперь мы подошли к доказательству. Мы разделяем r на две части: первая часть { 1, 2 } представляет линейную комбинацию столбцов внутри строки, а вторая часть { 3, 4 } представляет линейную комбинацию строк. Мы вычисляем тензорное произведение и для столбцов:

Для части строки:

Это означает: список всех возможных продуктов определенного значения в каждом наборе. В случае строки мы получаем:

[( 1-r 2)*( 1-r 3), ( 1-r 3), ( 1-r 2)*r 3, r 2*r 3 ]

При r = { 1, 2, 3, 4 } (поэтому r 2 = 3 и r 3 = 4):

[( 1-3)*( 1-4), 3*( 1-4),( 1-3)* 4, 3* 4 ] = [ 6, -9 -8 -12 ]

Теперь мы вычисляем новую строку t, взяв линейную комбинацию существующих строк. То есть берем:

Вы можете думать о том, что здесь происходит, как о частичной оценке. Если мы умножим полное тензорное произведение на полный вектор всех значений, вы получите вычисление P(1, 2, 3, 4) = -137. Здесь мы умножили частичное тензорное произведение, используя только половину оценочных координат, и сократили сетку N значений до одной строки значений квадратного корня N. Если вы передадите эту строку кому-то другому, он сможет выполнить остальную часть вычислений, используя тензорное произведение другой половины оценочных координат.

Доказывающая сторона предоставляет проверяющему следующую новую строку: t и доказательство Меркла для некоторых случайно выбранных столбцов. В нашем иллюстративном примере средство доказательства предоставит только последний столбец; в реальной жизни проверяющему придется предоставить десятки столбцов для достижения адекватной безопасности.

Теперь мы воспользуемся линейностью кодов Рида-Соломона. Ключевое свойство, которое мы используем, заключается в том, что использование линейной комбинации разложений Рида-Соломона дает тот же результат, что и разложение Рида-Соломона линейной комбинации. Эта последовательная независимость обычно возникает, когда обе операции линейны.

Верификатор делает именно это. Они вычисляют t и вычисляют линейные комбинации тех же столбцов, которые доказыватель вычислил ранее (но только столбцов, предоставленных доказывающим), и проверяют, что две процедуры дают одинаковый ответ.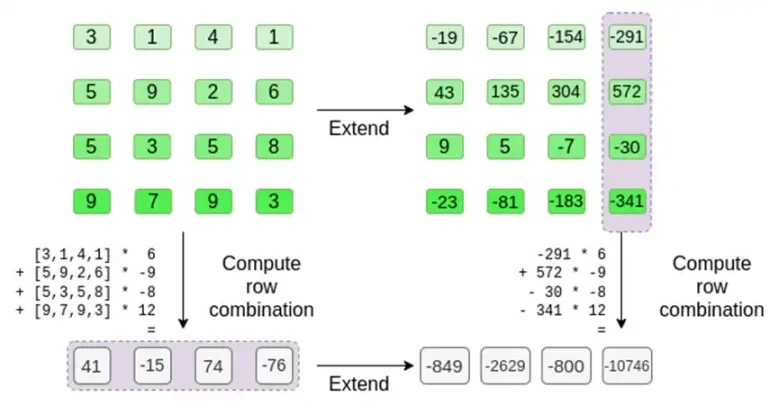

В этом случае мы расширяем t и вычисляем одну и ту же линейную комбинацию ([6,-9,-8, 12]), которые дают один и тот же ответ: -10746. Это доказывает, что корень Меркла был построен добросовестно (или, по крайней мере, достаточно близко) и что он соответствует t: по крайней мере, подавляющее большинство столбцов совместимы друг с другом.

Но есть еще одна вещь, которую проверяющему необходимо проверить: проверить оценку многочлена {r 0 …r 3 }. До сих пор все шаги проверяющего фактически не зависели от значения, заявленного проверяющим. Вот как мы это проверяем. Берем тензорное произведение «части столбца», которое мы отметили как точку расчета: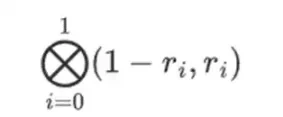

В нашем случае, где r = { 1, 2, 3, 4 }, поэтому половина выбранных столбцов равна { 1, 2 }), это эквивалентно:

Теперь возьмем эту линейную комбинацию t:

Это то же самое, что и непосредственное решение многочлена.

Вышеизложенное очень близко к полному описанию простого протокола Binius. Это уже имеет некоторые интересные преимущества: например, поскольку данные разделены на строки и столбцы, вам нужно только поле вдвое меньшего размера. Однако это не обеспечивает всех преимуществ вычислений в двоичном формате. Для этого нам нужен полный протокол Binius. Но сначала давайте более подробно рассмотрим двоичные поля.

Двоичные поля

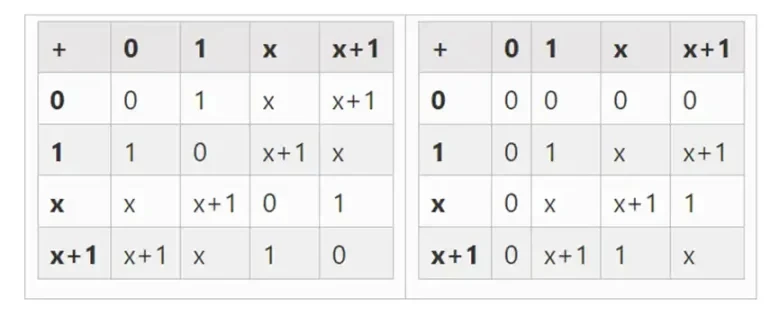
Наименьшее возможное поле — это арифметическое поле по модулю 2, которое настолько мало, что для него можно написать таблицы сложения и умножения:

Мы можем получить более крупные двоичные поля путем расширения: если мы начнем с F 2 (целые числа по модулю 2), а затем определим x, где x в квадрате = x + 1, мы получим следующие таблицы сложения и умножения:

Оказывается, повторив эту конструкцию, мы можем расширить бинарные поля до сколь угодно больших размеров. В отличие от комплексных чисел вместо действительных чисел, где вы можете добавить новый элемент, но никогда не добавлять больше элементов I (кватернионы существуют, но они математически странные, например, ab не равно ba), с конечными полями вы можете добавлять новые расширения навсегда. В частности, наше определение элемента выглядит следующим образом: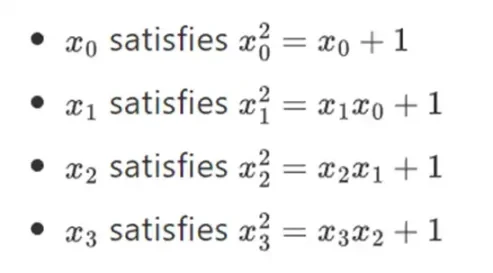

И так далее… Это часто называют башенной конструкцией, потому что каждое последующее расширение можно рассматривать как добавление к башне нового слоя. Это не единственный способ создания двоичных полей произвольного размера, но он имеет некоторые уникальные преимущества, которые использует Binius.

Мы можем представить эти числа в виде списков битов. Например, 1100101010001111. Первый бит представляет кратное 1, второй бит представляет кратное x0, а затем следующие биты представляют кратное x1: x1, x1*x0, x2, x2*x0 и так далее. Эта кодировка удобна тем, что ее можно разбить на части:

Это относительно необычное обозначение, но мне нравится представлять элементы двоичного поля как целые числа, с более эффективным битом справа. То есть 1 = 1, x0 = 01 = 2, 1+x0 = 11 = 3, 1+x0+x2 = 11001000 = 19 и так далее. В этом представлении это 61779.

Сложение в двоичном поле — это просто XOR (как, кстати, и вычитание); обратите внимание, что это означает x+x = 0 для любого x. Чтобы перемножить два элемента x*y, существует очень простой рекурсивный алгоритм: разделите каждое число пополам:

Затем разделите умножение:

Последняя часть — единственная, которая немного сложна, потому что вам придется применять правила упрощения. Существуют более эффективные способы умножения, подобные алгоритму Карацубы и быстрому преобразованию Фурье, но я оставлю это в качестве упражнения, чтобы заинтересованный читатель мог разобраться.

Деление в двоичных полях осуществляется путем совмещения умножения и инверсии. Простой, но медленный метод обращения представляет собой применение обобщенной малой теоремы Ферма. Существует также более сложный, но более эффективный алгоритм инверсии, который вы можете найти здесь. Вы можете использовать этот код для экспериментов со сложением, умножением и делением двоичных полей.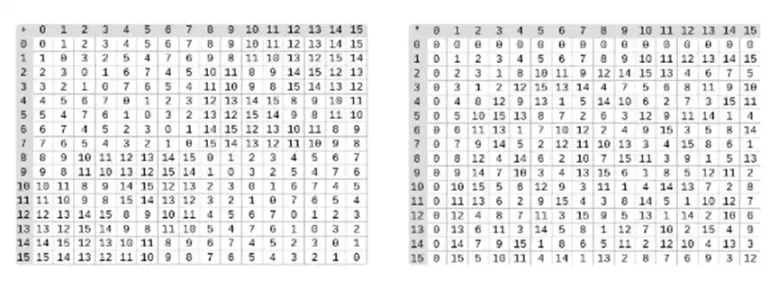

Слева: таблица сложения для четырехбитных элементов двоичного поля (т. е. только 1, x 0, x 1, x 0x 1). Справа: таблица умножения для четырехбитных элементов двоичного поля.

Прелесть этого типа двоичных полей в том, что они сочетают в себе лучшие стороны обычных целых чисел и модульной арифметики. Как и обычные целые числа, элементы двоичного поля не ограничены: вы можете увеличивать их до любого размера. Но, как и в случае с модульной арифметикой, если вы оперируете значениями в пределах определенного размера, все ваши результаты останутся в том же диапазоне. Например, если вы возведете число 42 в последовательные степени, вы получите:

После 255 шагов вы возвращаетесь к числу 42 в степени 255 = 1, и, как положительные целые числа и модульные операции, они подчиняются обычным законам математики: a*b=b*a, a*(b+c)= a*b+a*c и даже некоторые странные новые законы.

Наконец, двоичные поля удобны для манипулирования битами: если вы выполняете математические операции с числами, умещающимися в 2 КБ, то весь ваш вывод также уместится в 2 КБ бит. Это позволяет избежать неловкости. В Ethereums EIP-4844 отдельные блоки BLOB-объекта должны быть числами по модулю 52435875175126190479447740508185965837690552500527637822603658699938581184513, поэтому для кодирования двоичных данных требуется выбросить некоторое пространство и выполнить дополнительные проверки. прикладной уровень, чтобы гарантировать, что значение, хранящееся в каждом элементе, меньше 2248. Это Это также означает, что операции с двоичными полями выполняются на компьютерах очень быстро — как на процессорах, так и на теоретически оптимальных конструкциях FPGA и ASIC.

Все это означает, что мы можем выполнить кодирование Рида-Соломона, как мы это делали выше, таким образом, чтобы полностью избежать целочисленного взрыва, как мы видели в нашем примере, и очень естественным образом выполнять те вычисления, с которыми хорошо справляются компьютеры. Свойство разделения двоичных полей — как мы можем сделать 1100101010001111 = 11001010 + 10001111*x 3 , а затем разделить его по мере необходимости — также имеет решающее значение для обеспечения большей гибкости.

Полный Биниус

Видеть здесь для реализации протокола на Python.

Теперь мы можем перейти к «полному Биниусу», который адаптирует «простой Биниус» для (i) работы с двоичными полями и (ii) позволяет нам фиксировать отдельные биты. Этот протокол трудно понять, поскольку он переключается между разными способами рассмотрения битовых матриц; мне определенно потребовалось больше времени, чтобы понять это, чем обычно требуется для понимания криптографических протоколов. Но как только вы поймете двоичные поля, хорошая новость заключается в том, что «более сложной математики», на которую опирается Биниус, не существует. Это не пары эллиптических кривых, в которых есть все более и более глубокие кроличьи норы алгебраической геометрии, в которые можно проникнуть; здесь у вас просто двоичные поля.

Давайте еще раз посмотрим на полную диаграмму:

К этому моменту вы должны быть знакомы с большинством компонентов. Идея сведения гиперкуба в сетку, идея вычисления комбинаций строк и столбцов как тензорных произведений точек оценки, а также идея проверки эквивалентности между расширением Рида-Соломона, затем вычислением комбинаций строк и вычислением комбинаций строк, а затем расширением Рида-Соломона. все они реализованы в простом Binius.

Что нового в Complete Binius? В основном три вещи:

• Отдельные значения в гиперкубе и квадрате должны быть битами (0 или 1).

• Процесс расширения расширяет биты до большего количества битов, группируя их в столбцы и временно предполагая, что они являются элементами более крупного поля.

• После этапа объединения строк следует этап поэлементного разложения на биты, который преобразует расширение обратно в биты.

Мы обсудим оба случая по очереди. Во-первых, новая процедура продления. Коды Рида-Соломона имеют фундаментальное ограничение: если вы хотите расширить n до k*n, вам нужно работать в поле с k*n различными значениями, которые можно использовать в качестве координат. С F 2 (он же бит) этого сделать невозможно. Итак, что мы делаем, так это упаковываем соседние элементы F 2 вместе, чтобы сформировать более крупные значения. В приведенном здесь примере мы упаковываем по два бита в элементы { 0 , 1 , 2 , 3 } , чего нам достаточно, поскольку наше расширение имеет только четыре вычислительные точки. В реальном доказательстве мы могли бы вернуться на 16 бит за раз. Затем мы выполняем код Рида-Соломона для этих упакованных значений и снова распаковываем их в биты.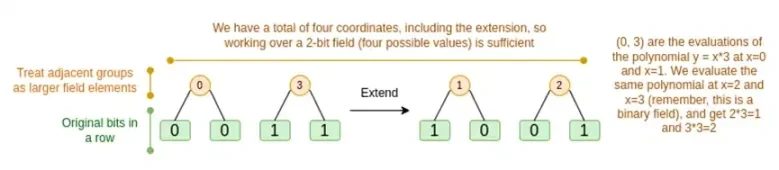

Теперь комбинации строк. Чтобы сделать проверку случайной точки криптографически безопасной, нам нужно выбрать эту точку из довольно большого пространства (намного большего, чем сам гиперкуб). Таким образом, хотя точка внутри гиперкуба является битом, вычисленное значение вне гиперкуба будет намного больше. В приведенном выше примере комбинация строк оказывается [11, 4, 6, 1].

Это представляет собой проблему: мы знаем, как сгруппировать биты в большее значение, а затем выполнить расширение Рида-Соломона для этого значения, но как нам сделать то же самое для больших пар значений?

Хитрость Биниуса заключается в том, чтобы делать это постепенно: мы смотрим на один бит каждого значения (например, для объекта, который мы пометили 11, это [1, 1, 0, 1]), а затем разворачиваем его строка за строкой. То есть мы разворачиваем его на 1 строку каждого элемента, затем на строку х0, затем на строку х1, затем на строку х0х1 и так далее (ну, в нашем игрушечном примере мы на этом останавливаемся, а в реальном реализация может увеличиться до 128 строк (последняя будет x6*…*x0))

обзор:

• Преобразуем биты в гиперкубе в сетку

• Затем мы рассматриваем группы соседних битов в каждой строке как элементы большего поля и выполняем над ними арифметические операции, чтобы расширить строку Рида-Соломона.

• Затем мы берем комбинацию строк каждого столбца битов и получаем на выходе столбец битов для каждой строки (намного меньший для квадратов размером более 4 x 4).

• Затем мы рассматриваем выходные данные как матрицу, а ее биты — как строки.

Почему это происходит? В обычной математике, если вы начнете дробить число побитно, (обычная) способность выполнять линейные операции в любом порядке и получать один и тот же результат нарушается. Например, если я начну с числа 345 и умножу его на 8, затем на 3, я получу 8280, а если я проделаю эти две операции в обратном порядке, я также получу 8280. Но если я вставлю операцию нарезки битов между двумя шагами все ломается: если вы сделаете 8x, затем 3x, вы получите: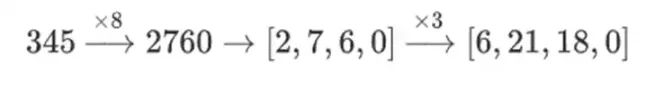

Но если вы сделаете 3 раза, а затем 8 раз, вы получите:

Но в бинарных полях, построенных на основе башенных структур, этот подход действительно работает. Причина в их разделимости: если вы умножите большое значение на маленькое, то, что происходит в каждом сегменте, останется в каждом сегменте. Если мы умножим 1100101010001111 на 11, это будет то же самое, что и первое разложение 1100101010001111, то есть

Затем умножьте каждый компонент на 11.

Собираем все это вместе

В общем, системы доказательства с нулевым разглашением работают, делая утверждения о полиноме, которые одновременно представляют собой утверждения об основной оценке: точно так же, как мы видели в примере Фибоначчи, F(X+ 2)-F(X+ 1)-F( X) = Z(X)*H(X) при проверке всех шагов расчета Фибоначчи. Мы проверяем утверждения о полиноме, доказывая оценку в случайных точках. Эта проверка случайных точек представляет собой проверку всего многочлена: если полиномиальное уравнение не совпадает, существует небольшая вероятность того, что оно совпадает по определенной случайной координате.

На практике одним из основных источников неэффективности является то, что в реальных программах большинство чисел, с которыми мы имеем дело, невелики: индексы в циклах for, значения True/False, счетчики и тому подобное. Однако когда мы расширяем данные с помощью кодировки Рида-Соломона, чтобы обеспечить избыточность, необходимую для обеспечения безопасности проверок на основе Меркла, большинство дополнительных значений в конечном итоге занимают весь размер поля, даже если исходное значение было небольшим.

Чтобы это исправить, мы хотим сделать это поле как можно меньшим. Plonky 2 перевел нас от 256-битных чисел к 64-битным, а затем Plonky 3 еще больше снизил их до 31 бита. Но даже это не оптимально. В двоичных полях мы можем иметь дело с отдельными битами. Это делает кодирование плотным: если ваши фактические базовые данные имеют n бит, тогда ваша кодировка будет иметь n бит, а расширение будет иметь 8*n бит без каких-либо дополнительных затрат.

Теперь давайте посмотрим на этот график в третий раз:

В Биниусе мы работаем с полилинейным полиномом: гиперкубом P(x0, x1,…xk), где отдельные оценки P(0, 0, 0, 0), P(0, 0, 0, 1) до P( 1, 1, 1, 1), хранят данные, которые нас интересуют. Чтобы доказать вычисление в определенной точке, мы интерпретируем те же данные как квадрат. Затем мы расширяем каждую строку, используя кодировку Рида-Соломона, чтобы обеспечить избыточность данных, необходимую для защиты от рандомизированных запросов ветвей Меркла. Затем мы вычисляем случайные линейные комбинации строк, разрабатывая коэффициенты так, чтобы новая объединенная строка фактически содержала нужное нам вычисленное значение. Эта вновь созданная строка (переинтерпретированная как 128-битная строка) и несколько случайно выбранных столбцов с ветвями Меркла передаются верификатору.

Затем верификатор выполняет комбинацию расширенных строк (или, точнее, расширенных столбцов) и комбинацию расширенных строк и проверяет их совпадение. Затем он вычисляет комбинацию столбцов и проверяет, возвращает ли она значение, заявленное доказывающим. Это наша система доказательств (или, точнее, схема полиномиального обязательства, которая является ключевым компонентом системы доказательств).

Что мы еще не рассмотрели?

• Чтобы сделать валидатор эффективным в вычислительном отношении, необходим эффективный алгоритм расширения строк. Мы используем быстрое преобразование Фурье для двоичных полей, описанное здесь (хотя точная реализация будет другой, поскольку в этом посте используется менее эффективная конструкция, не основанная на рекурсивном расширении).

• Арифметически. Одномерные полиномы удобны, поскольку вы можете выполнять такие действия, как F(X+2)-F(X+1)-F(X) = Z(X)*H(X), чтобы связать соседние шаги вычислений. В гиперкубе следующий шаг объяснен гораздо хуже, чем X+1. Вы можете использовать X+k, степени k, но такое поведение прыжков приносит в жертву многие ключевые преимущества Биниуса. В статье Биниуса описано решение. См. раздел 4.3), но это само по себе глубокая кроличья нора.

• Как безопасно выполнять определенные проверки значений. Пример Фибоначчи требовал проверки ключевых граничных условий: значений F(0)=F(1)=1 и F(100). Но для оригинального Биниуса небезопасно проводить проверки в известных точках расчета. Существует несколько довольно простых способов преобразования известных проверок вычислений в неизвестные проверки вычислений, используя так называемые протоколы проверки сумм; но мы не будем рассматривать их здесь.

• Протоколы поиска — еще одна широко используемая в последнее время технология — используются для создания сверхэффективных систем доказательств. Binius можно использовать в сочетании с протоколами поиска для многих приложений.

• За пределами времени проверки квадратного корня. Квадратные корни стоят дорого: доказательство Биниуса из 2^32 бит занимает около 11 МБ. Вы можете компенсировать это, используя другие системы доказательств для доказательства доказательств Биниуса, что дает вам эффективность доказательства Биниуса с меньшим размером доказательства. Другой вариант — более сложный протокол FRI-Binius, который создает доказательство мультилогарифмического размера (как и обычный FRI).

• Как Биниус влияет на дружелюбие к СНАРКу. Основной вывод заключается в том, что если вы используете Binius, вам больше не нужно заботиться о том, чтобы сделать вычисления удобными для арифметики: обычное хеширование больше не более эффективно, чем традиционное арифметическое хэширование, умножение по модулю 2 в степени 32 или по модулю 2 в степени . 256 уже не так мучительно, как умножение по модулю 2 и т. д. Но это сложная тема. Многое меняется, когда все делается в двоичном формате.

Я ожидаю увидеть больше улучшений в технологии доказательства на основе двоичных полей в ближайшие месяцы.

Источником этой статьи является Интернет: Виталик: Биниус, эффективные доказательства для бинарных полей.

Связанный: Монета BNB показывает признаки восстановления: новогодний максимум на площадке

Вкратце, цена BNB отскочила от $550 и приблизилась на дюйм к пробитию сопротивления $593. Ценовые индикаторы вновь обрели бычий импульс, что поддерживает рост 8%. Коэффициент Шарпа на уровне 4,03, вероятно, привлечет новых инвесторов к биржевому токену. Март был благоприятным месяцем для BNB Coin: всего за несколько дней криптовалюта достигла двух новых максимумов за год, прежде чем произошла коррекция. После почти двухнедельного периода восстановления BNB Coin демонстрирует признаки потенциального достижения нового максимума в 2024 году. Но достижима ли такая веха? BNB выглядит многообещающе. После отскока от уровня поддержки $550 стоимость монеты BNB выросла до $581 на момент проведения этого анализа. Это улучшение отражает восстановление профиля риска и доходности альткойна,…