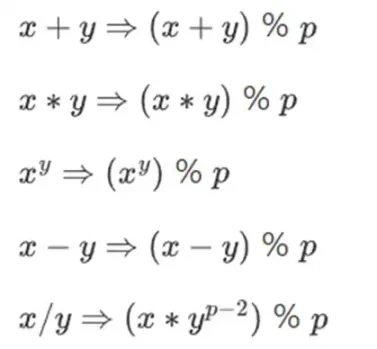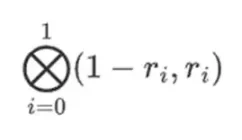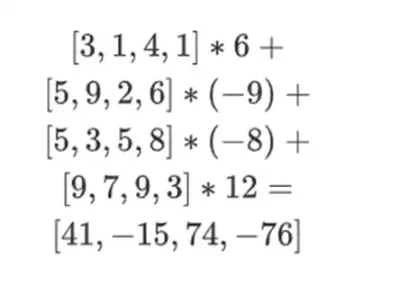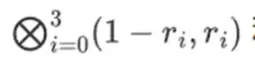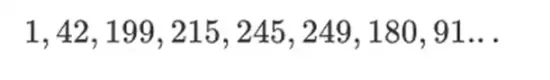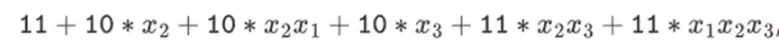Vitalik: Binius, 이진 필드에 대한 효율적인 증명

원본 기사: Vitalik Buterin

원문: Kate, MarsBit

이 게시물은 주로 2019년 암호화, 특히 SNARK 및 STARK에 일반적으로 익숙한 독자를 위한 것입니다. 그렇지 않은 경우 해당 내용을 먼저 읽어 보시기 바랍니다. 피드백과 의견을 주신 Justin Drake, Jim Posen, Benjamin Diamond 및 Radi Cojbasic에게 특별히 감사드립니다.

지난 2년 동안 STARK는 매우 복잡한 진술(예: Ethereum 블록이 유효함을 증명)에 대한 쉽게 검증 가능한 암호화 증명을 효율적으로 만드는 데 핵심적이고 대체할 수 없는 기술이 되었습니다. 이에 대한 주요 이유 중 하나는 작은 필드 크기입니다. 타원 곡선을 기반으로 하는 SNARK는 충분히 안전하기 위해 256비트 정수로 작업해야 하는 반면, STARK를 사용하면 훨씬 더 작은 필드 크기를 더 높은 효율성으로 사용할 수 있습니다. 먼저 Goldilocks 필드(64비트 정수), 그 다음 Mersenne 31 및 BabyBear(둘 다 31비트)입니다. 이러한 효율성 향상으로 인해 Goldilocks를 사용하는 Plonky 2는 여러 종류의 계산을 증명하는 데 이전 버전보다 수백 배 더 빠릅니다.

자연스러운 질문은 다음과 같습니다. 이러한 추세를 논리적 결론으로 끌어내고 0과 1에서 직접 작동하여 더 빠르게 실행되는 증명 시스템을 구축할 수 있습니까? 이것이 바로 Binius가 3년 전의 SNARK 및 STARK와 매우 다른 여러 수학적 트릭을 사용하여 시도하는 것입니다. 이 게시물에서는 작은 필드가 증명 생성을 더 효율적으로 만드는 이유, 이진 필드가 독특하게 강력한 이유, Binius가 이진 필드에 대한 증명을 매우 효율적으로 만들기 위해 사용하는 트릭에 대해 설명합니다.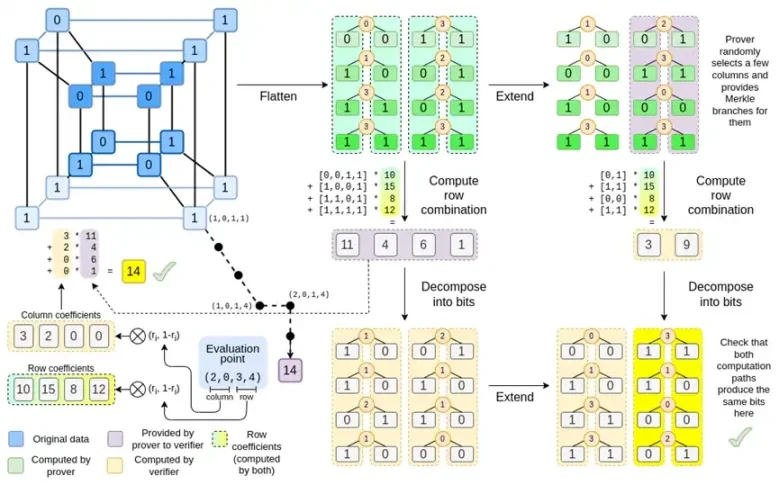

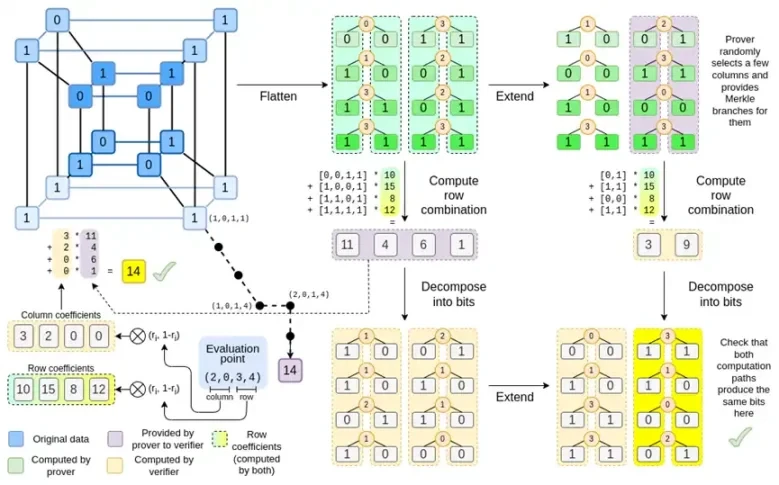
Binius님, 이 게시물이 끝날 때쯤이면 이 다이어그램의 모든 부분을 이해할 수 있을 것입니다.

검토: 유한 필드

암호화 증명 시스템의 주요 작업 중 하나는 숫자를 작게 유지하면서 많은 양의 데이터를 처리하는 것입니다. 큰 프로그램에 대한 설명을 몇 개의 숫자가 포함된 수학 방정식으로 압축할 수 있지만 그 숫자가 원래 프로그램만큼 크다면 아무 것도 얻을 수 없습니다.

숫자를 작게 유지하면서 복잡한 산술을 수행하기 위해 암호 작성자는 모듈러 산술을 사용하는 경우가 많습니다. 우리는 소수 모듈러스 p를 선택합니다. % 연산자는 나머지를 취함을 의미합니다: 15% 7 = 1, 53% 10 = 3 등. (답은 항상 음수가 아닙니다. 예를 들어 -1% 10 = 9입니다.)

시간을 더하고 빼는 맥락에서 모듈러 연산을 본 적이 있을 것입니다(예: 9시 이후 4시간은 몇시입니까?). 하지만 여기서는 모듈로 숫자를 더하고 빼는 것이 아닙니다. 곱셈, 나눗셈, 지수를 취할 수도 있습니다.

우리는 다음을 재정의합니다:

위의 규칙은 모두 일관성이 있습니다. 예를 들어 p = 7이면 다음과 같습니다.

5 + 3 = 1(8% 7 = 1이기 때문에)

1-3 = 5 (-2% 7 = 5이기 때문에)

2* 5 = 3

3/5 = 2

이러한 구조에 대한 보다 일반적인 용어는 유한 필드입니다. 유한체(Finite Field)는 일반적인 산술 법칙을 따르지만 가능한 값의 개수가 유한하여 각 값이 고정된 크기로 표현될 수 있는 수학적 구조입니다.

모듈러 산술(또는 소수 필드)은 가장 일반적인 유형의 유한 필드이지만 확장 필드라는 또 다른 유형도 있습니다. 하나의 확장 필드인 복소수를 본 적이 있을 것입니다. 우리는 새로운 요소를 상상하고 그것에 i라는 라벨을 붙이고 그것으로 수학을 합니다: (3i+2)*(2i+4)=6i*i+12i+4i+8=16i+2. 프라임 필드의 확장으로도 동일한 작업을 수행할 수 있습니다. 더 작은 필드를 다루기 시작하면서 보안을 위해 프라임 필드의 확장이 점점 더 중요해지며 바이너리 필드(Binius에서 사용)는 실용적인 유용성을 위해 전적으로 확장에 의존합니다.

검토: 산술화

SNARK 및 STARK가 컴퓨터 프로그램을 증명하는 방식은 산술을 통해 이루어집니다. 즉, 증명하려는 프로그램에 대한 설명을 취하고 이를 다항식을 포함하는 수학 방정식으로 변환합니다. 방정식에 대한 유효한 해는 프로그램의 유효한 실행에 해당합니다.

간단한 예로, 제가 100번째 피보나치 수를 계산했고 그것이 무엇인지 증명하고 싶다고 가정해 보겠습니다. 나는 피보나치 수열을 인코딩하는 다항식 F를 만듭니다. 따라서 F(0)=F(1)=1, F(2)=2, F(3)=3, F(4)=5 등 100단계 동안 계속됩니다. . 제가 증명해야 할 조건은 전체 범위 x={0, 1…98}에 걸쳐 F(x+2)=F(x)+F(x+1)입니다. 나는 당신에게 다음의 몫을 줌으로써 당신을 설득할 수 있습니다:

여기서 Z(x) = (x-0) * (x-1) * …(x-98)입니다. . F와 H가 이 방정식을 만족한다고 제공할 수 있다면 F는 범위에서 F(x+ 2)-F(x+ 1)-F(x)를 충족해야 합니다. F에 대해 F(0)=F(1)=1임을 추가로 확인하면 F(100)은 실제로 100번째 피보나치 수여야 합니다.

더 복잡한 것을 증명하려면 간단한 관계 F(x+2) = F(x) + F(x+1)를 기본적으로 F(x+1)이 출력이라고 말하는 더 복잡한 방정식으로 바꾸세요. 상태 F(x)로 가상 머신을 초기화하고 하나의 계산 단계를 실행합니다. 더 많은 단계를 수용하기 위해 숫자 100을 더 큰 숫자(예: 100000000)로 바꿀 수도 있습니다.

모든 SNARK 및 STARK는 다항식(때로는 벡터 및 행렬)에 대한 간단한 방정식을 사용하여 개별 값 간의 수많은 관계를 표현한다는 아이디어를 기반으로 합니다. 모든 알고리즘이 위와 같이 인접한 계산 단계 간의 동등성을 확인하는 것은 아닙니다. 예를 들어 PLONK는 그렇지 않으며 R1CS도 마찬가지입니다. 그러나 가장 효과적인 검사 중 다수는 그렇게 합니다. 동일한 검사(또는 동일한 소수의 검사)를 여러 번 수행하면 오버헤드를 최소화하는 것이 더 쉽기 때문입니다.

Plonky 2: 256비트 SNARK 및 STARK에서 64비트까지… STARK만

5년 전, 다양한 유형의 영지식 증명에 대한 합리적인 요약은 다음과 같습니다. 증명에는 (타원 곡선 기반) SNARK와 (해시 기반) STARK의 두 가지 유형이 있습니다. 기술적으로 STARK는 SNARK의 한 유형이지만 실제로는 "SNARK"를 사용하여 타원 곡선 기반 변형을 나타내고 "STARK"를 해시 기반 구성을 나타내는 것이 일반적입니다. SNARK는 크기가 작기 때문에 매우 빠르게 검증하고 온체인에 쉽게 설치할 수 있습니다. STARK는 크기가 크지만 신뢰할 수 있는 설정이 필요하지 않으며 양자 저항성이 있습니다.

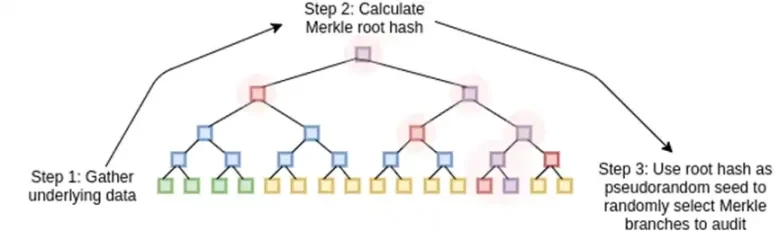
STARK는 데이터를 다항식으로 처리하고 해당 다항식의 계산을 계산하며 확장된 데이터의 머클 루트를 "다항식 약속"으로 사용하여 작동합니다.

여기서 중요한 역사는 타원 곡선 기반 SNARK가 먼저 널리 사용되었다는 것입니다. STARK는 FRI 덕분에 2018년경까지 충분히 효율적이지 않았고 그때까지 Zcash는 1년 넘게 운영되었습니다. 타원 곡선 기반 SNARK에는 주요 제한 사항이 있습니다. 타원 곡선 기반 SNARK를 사용하려는 경우 이러한 방정식의 산술은 타원 곡선의 점 수에 대해 모듈로 수행되어야 합니다. 이는 일반적으로 2의 256제곱에 가까운 큰 숫자입니다. 예를 들어 bn128 곡선의 경우 21888242871839275222246405745257275088548364400416034343698204186575808495617입니다. 그러나 실제 컴퓨팅에서는 작은 숫자를 사용합니다. 당신이 가장 좋아하는 언어로 된 실제 프로그램에 대해, 대부분의 내용은 카운터, for 루프의 인덱스, 프로그램의 위치, True 또는 False를 나타내는 단일 비트 및 거의 항상 몇 자릿수 길이인 기타 항목이 사용됩니다.

원본 데이터가 작은 숫자로 구성되어 있더라도 증명 프로세스에는 평균적으로 전체 크기와 같거나 더 큰 수의 객체를 생성하는 몫, 확장, 무작위 선형 조합 및 기타 데이터 변환 계산이 필요합니다. 필드. 이로 인해 중요한 비효율성이 발생합니다. n개의 작은 값에 대한 계산을 증명하려면 훨씬 더 큰 n개의 값에 대해 더 많은 계산을 수행해야 합니다. 처음에 STARK는 256비트 필드를 사용하는 SNARK 습관을 물려받았으므로 동일한 비효율성을 겪었습니다.

일부 다항식 평가의 리드 솔로몬 확장. 원래 값이 작더라도 추가 값은 필드의 전체 크기(이 경우 2^31 – 1)로 확장됩니다.

2022년에는 Plonky 2가 출시되었습니다. Plonky 2의 주요 혁신은 더 작은 소수(2의 64제곱 – 2의 32제곱 + 1 = 18446744067414584321)로 산술 모듈로 연산을 수행하는 것입니다. 이제 각각의 덧셈이나 곱셈은 항상 몇 가지 명령어로 수행할 수 있습니다. CPU 및 모든 데이터를 함께 해싱하는 속도가 이전보다 4배 빠릅니다. 하지만 문제가 있습니다. 이 방법은 STARK에만 작동합니다. SNARK를 사용하려고 하면 타원 곡선은 이러한 작은 타원 곡선에 대해 안전하지 않게 됩니다.

보안을 보장하기 위해 Plonky 2에는 확장 필드도 도입해야 합니다. 산술 방정식을 확인하는 핵심 기술은 무작위 점 샘플링입니다. H(x) * Z(x)가 F(x+ 2)-F(x+ 1)-F(x)와 같은지 확인하려면 무작위로 다음을 수행할 수 있습니다. 좌표 r을 선택하고, H(r), Z(r), F(r), F(r+ 1) 및 F(r+ 2)를 증명하기 위한 다항식 공약을 제공한 다음 H(r) * Z(r)인지 확인합니다. )는 F(r+ 2)-F(r+ 1)- F(r)과 같습니다. 공격자가 좌표를 미리 추측할 수 있다면 공격자는 증명 시스템을 속일 수 있습니다. 이것이 증명 시스템이 무작위여야 하는 이유입니다. 그러나 이는 또한 공격자가 무작위로 추측할 수 없을 만큼 충분히 큰 세트에서 좌표를 샘플링해야 함을 의미합니다. 이는 모듈러스가 2의 256제곱에 가까우면 분명히 사실입니다. 그러나 모듈러스 2^64 – 2^32 + 1의 경우 아직 거기에 도달하지 않았으며 다음으로 내려가면 확실히 그렇지 않습니다. 2^31 – 1. 운이 좋을 때까지 증명을 20억 번 위조하려고 시도하는 것은 공격자의 능력 내에 있습니다.

이를 방지하기 위해 확장 필드에서 r을 샘플링합니다. 예를 들어 y^3 = 5인 경우 y를 정의하고 1, y 및 y^2의 조합을 사용할 수 있습니다. 이렇게 하면 총 좌표 수가 약 2^93이 됩니다. 증명자가 계산한 대부분의 다항식은 이 확장된 필드에 포함되지 않습니다. 그들은 단지 2^31-1 모듈로의 정수이므로 작은 필드를 사용하여 여전히 모든 효율성을 얻을 수 있습니다. 그러나 무작위 포인트 검사와 FRI 계산은 필요한 보안을 얻기 위해 이 더 큰 필드에 도달합니다.

작은 소수부터 이진수까지

컴퓨터는 더 큰 숫자를 0과 1의 시퀀스로 표현하고 해당 비트 위에 회로를 구축하여 덧셈과 곱셈과 같은 연산을 계산함으로써 산술을 수행합니다. 컴퓨터는 특히 16, 32, 64비트 정수에 최적화되어 있습니다. 예를 들어, 2^64 – 2^32 + 1 및 2^31 – 1은 해당 범위에 맞을 뿐만 아니라 해당 범위 내에 잘 맞기 때문에 선택되었습니다. 곱셈 모듈로 2^64 – 2^32 + 1 일반적인 32비트 곱셈을 수행하고 출력을 몇 군데에서 비트 단위로 이동하고 복사하여 수행할 수 있습니다. 이 기사에서는 몇 가지 요령을 잘 설명합니다.

그러나 훨씬 더 나은 접근 방식은 계산을 이진수로 직접 수행하는 것입니다. 한 비트에서 다음 비트로 1 + 1을 추가할 때 발생하는 이월에 대해 걱정할 필요 없이 추가가 단지 XOR일 수 있다면 어떨까요? 같은 방식으로 곱셈을 더 병렬화할 수 있다면 어떨까요? 이러한 장점은 모두 단일 비트로 참/거짓 값을 표현할 수 있다는 점에 기반합니다.

이진 계산을 직접 수행하여 이러한 이점을 얻는 것이 바로 Binius가 하려는 것입니다. Binius 팀은 zkSummit 프레젠테이션에서 효율성 향상을 입증했습니다.

대략 동일한 크기에도 불구하고 32비트 이진 필드에 대한 작업에는 31비트 메르센 필드에 대한 작업보다 5배 적은 계산 리소스가 필요합니다.

일변량 다항식에서 하이퍼큐브까지

우리가 이 추론을 믿고 비트(0과 1)로 모든 작업을 수행하고 싶다고 가정해 보겠습니다. 단일 다항식으로 어떻게 10억 비트를 표현할 수 있습니까?

여기서 우리는 두 가지 실질적인 문제에 직면합니다.

1. 다항식이 많은 수의 값을 나타내려면 다항식을 평가할 때 이러한 값에 접근할 수 있어야 합니다. 위의 피보나치 예에서는 F(0), F(1) … F(100), 그리고 더 큰 계산에서는 , 지수는 수백만 달러가 될 것입니다. 우리가 사용하는 필드에는 이 크기의 숫자가 포함되어야 합니다.

2. Merkle 트리(모든 STARK와 마찬가지로)에서 커밋한 값을 증명하려면 Reed-Solomon 인코딩이 필요합니다. 예를 들어 중복성을 사용하여 값을 n에서 8n으로 확장하여 악의적인 증명자가 계산 중에 값을 위조하여 부정 행위를 하는 것을 방지합니다. 또한 이를 위해서는 충분히 큰 필드가 필요합니다. 백만 개의 값에서 800만 개의 값으로 확장하려면 다항식을 평가하기 위해 800만 개의 서로 다른 점이 필요합니다.

Binius의 핵심 아이디어는 이 두 가지 문제를 개별적으로 해결하고 동일한 데이터를 두 가지 다른 방식으로 표현함으로써 이를 해결하는 것입니다. 첫째, 다항식 자체입니다. 타원 곡선 기반 SNARK, 2019년 시대 STARK, Plonky 2 등과 같은 시스템은 일반적으로 하나의 변수인 F(x)에 대한 다항식을 처리합니다. 반면 Binius는 스파르탄 프로토콜에서 영감을 얻어 다변량 다항식(F(x 1, x 2,… xk))을 사용합니다. 실제로 우리는 각 xi가 0 또는 1인 계산의 하이퍼큐브에서 전체 계산 궤적을 나타냅니다. 예를 들어, 피보나치 수열을 표현하고 싶지만 여전히 이를 표현하기에 충분히 큰 필드를 사용하는 경우 다음을 수행할 수 있습니다. 처음 16개 시퀀스를 다음과 같이 상상해 보세요.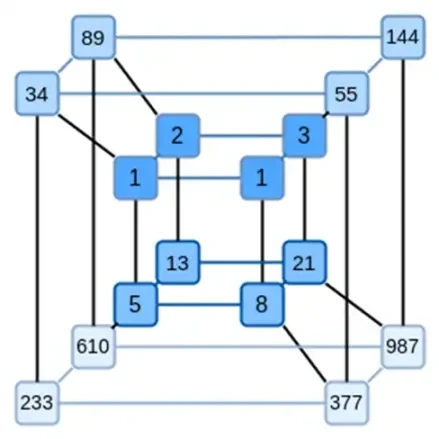

즉, F(0,0,0,0)은 1이어야 하고, F(1,0,0,0)도 1이고, F(0,1,0,0)은 2 등입니다. 최대 F(1,1,1,1) = 987입니다. 이러한 계산의 하이퍼큐브가 주어지면 이러한 계산을 생성하는 다변량 선형(각 변수의 1차) 다항식이 있습니다. 따라서 우리는 이 값 세트를 다항식을 나타내는 것으로 생각할 수 있습니다. 우리는 계수를 계산할 필요가 없습니다.

물론 이 예는 설명을 위한 것일 뿐입니다. 실제로 하이퍼큐브에 들어가는 전체 요점은 개별 비트를 처리하도록 하는 것입니다. 피보나치 수를 계산하는 Binius 기본 방법은 고차원 큐브를 사용하여 16비트 그룹당 하나의 숫자를 저장하는 것입니다. 비트 단위로 정수 추가를 구현하려면 약간의 영리함이 필요하지만 Binius의 경우 그리 어렵지 않습니다.

이제 삭제 코드를 살펴보겠습니다. STARK가 작동하는 방식은 n 값을 취하고 Reed-Solomon이 이를 더 많은 값(보통 8n, 일반적으로 2n에서 32n 사이)으로 확장한 다음 확장에서 일부 Merkle 분기를 무작위로 선택하고 일종의 확인을 수행하는 것입니다. 하이퍼큐브의 각 차원 길이는 2입니다. 따라서 이를 직접 확장하는 것은 실용적이지 않습니다. 16개 값에서 Merkle 분기를 샘플링할 공간이 충분하지 않습니다. 그럼 어떻게 해야 할까요? 하이퍼큐브가 정사각형이라고 가정해 봅시다!

Simple Binius – 예

보다 여기 프로토콜의 Python 구현을 위해.

편의를 위해 일반 정수를 필드로 사용하는 예를 살펴보겠습니다(실제 구현에서는 이진 필드 요소를 사용합니다). 먼저 제출하려는 하이퍼큐브를 정사각형으로 인코딩합니다.

이제 Reed-Solomon 방법을 사용하여 사각형을 확장합니다. 즉, 각 행을 x = { 0, 1, 2, 3 }에서 평가된 3차 다항식으로 처리하고 x = { 4, 5, 6, 7 }에서 동일한 다항식을 평가합니다.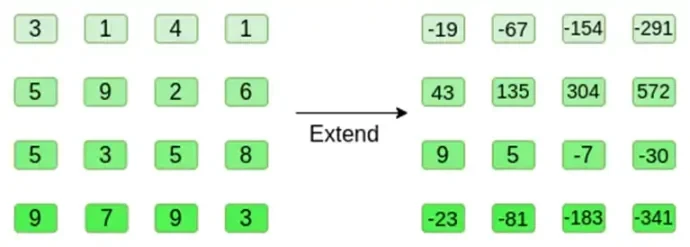

숫자가 정말 커질 수 있다는 점에 유의하세요! 이것이 실제 구현에서 일반 정수 대신 항상 유한 필드를 사용하는 이유입니다. 예를 들어 모듈로 11의 정수를 사용하면 첫 번째 행의 확장은 [3, 10, 0, 6]이 됩니다.

확장 기능을 사용해 보고 숫자를 직접 확인하려면 여기에서 간단한 Reed-Solomon 확장 코드를 사용할 수 있습니다.

다음으로, 이 확장을 열로 처리하고 해당 열의 머클 트리를 만듭니다. 머클 트리의 뿌리는 우리의 약속입니다.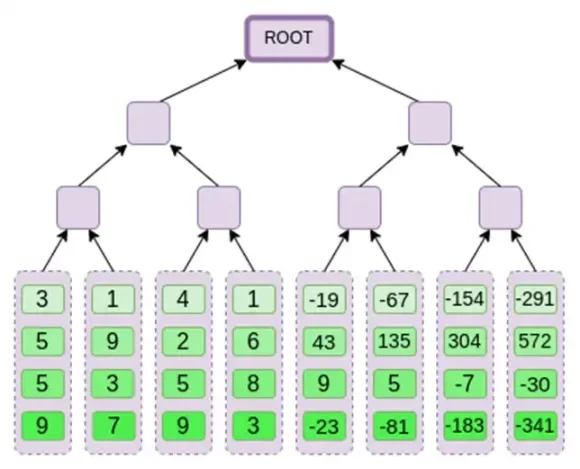

이제 증명자가 어떤 시점에서 이 다항식 r = {r 0, r 1, r 2, r 3 }의 계산을 증명하려고 한다고 가정해 보겠습니다. Binius에는 다른 다항식 확약 방식보다 약한 미묘한 차이가 있습니다. 증명자는 Merkle 루트에 커밋하기 전에 s를 알거나 추측할 수 없어야 합니다. 즉, r은 다음에 의존하는 의사 난수 값이어야 합니다. 머클 루트). 이로 인해 데이터베이스 조회에 이 체계가 쓸모 없게 됩니다(예를 들어, 당신이 나에게 Merkle 루트를 주었으니 이제 P(0, 0, 1, 0)를 증명해 보세요!). 그러나 우리가 실제로 사용하는 영지식 증명 프로토콜은 일반적으로 데이터베이스 조회가 필요하지 않습니다. 무작위 평가 지점에서 다항식을 확인하기만 하면 됩니다. 따라서 이 제한은 우리의 목적에 잘 부합합니다.

r = { 1, 2, 3, 4 }를 선택한다고 가정합니다(다항식은 -137로 평가됩니다. 이 코드를 사용하여 이를 확인할 수 있습니다). 이제 우리는 증거에 도달합니다. r을 두 부분으로 나눕니다. 첫 번째 부분 { 1, 2 }는 행 내 열의 선형 조합을 나타내고 두 번째 부분 { 3, 4 }는 행의 선형 조합을 나타냅니다. 텐서 곱과 열에 대해 계산합니다.

행 부분의 경우:

이는 각 세트에 있는 값의 가능한 모든 곱의 목록을 의미합니다. 행의 경우 다음을 얻습니다.

[( 1-r 2)*( 1-r 3), ( 1-r 3), ( 1-r 2)*r 3, r 2*r 3 ]

r = { 1, 2, 3, 4 }인 경우(따라서 r 2 = 3 및 r 3 = 4):

[( 1-3)*( 1-4), 3*( 1-4),( 1-3)* 4, 3* 4 ] = [ 6, -9 -8 -12 ]

이제 기존 행의 선형 조합을 사용하여 새 행 t를 계산합니다. 즉, 우리는 다음을 취합니다:

여기서 일어나는 일은 부분적인 평가라고 생각할 수 있습니다. 전체 텐서 곱에 모든 값의 전체 벡터를 곱하면 P(1, 2, 3, 4) = -137이라는 계산을 얻게 됩니다. 여기서는 평가 좌표의 절반만 사용하여 부분 텐서 곱을 곱하고 N 값의 그리드를 N 값의 제곱근 단일 행으로 줄였습니다. 이 행을 다른 사람에게 제공하면 평가 좌표의 나머지 절반에 대한 텐서 곱을 사용하여 나머지 계산을 수행할 수 있습니다.

증명자는 검증자에게 다음과 같은 새로운 행을 제공합니다: t 및 무작위로 샘플링된 일부 열의 Merkle 증명. 예시에서는 증명자가 마지막 열만 제공하도록 합니다. 실제 생활에서 증명자는 적절한 보안을 달성하기 위해 수십 개의 열을 제공해야 합니다.

이제 우리는 Reed-Solomon 코드의 선형성을 활용합니다. 우리가 활용하는 주요 특성은 리드-솔로몬 확장의 선형 조합을 취하면 선형 조합의 리드-솔로몬 확장을 취하는 것과 동일한 결과를 제공한다는 것입니다. 이러한 순차적 독립성은 일반적으로 두 작업이 모두 선형일 때 발생합니다.

검증인은 바로 그 일을 합니다. 그들은 t를 계산하고 증명자가 이전에 계산한 것과 동일한 열(그러나 증명자가 제공한 열만)의 선형 조합을 계산하고 두 프로시저가 동일한 답을 제공하는지 확인합니다.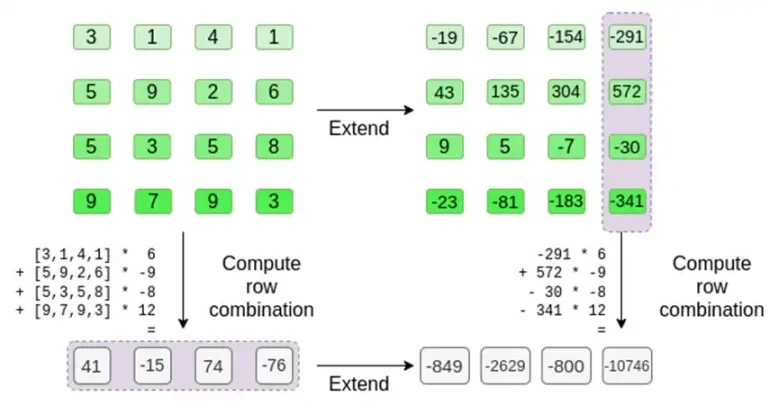

이 경우 t를 확장하고 동일한 선형 조합([6,-9,-8, 12])을 계산합니다. 둘 다 동일한 답(-10746)을 제공합니다. 이는 Merkle 루트가 선의로(또는 적어도 충분히 가깝게) 구성되었으며 t와 일치함을 증명합니다. 최소한 대다수의 열은 서로 호환됩니다.

하지만 검증자가 확인해야 할 것이 한 가지 더 있습니다. 다항식 {r 0 …r 3 }의 평가를 확인하세요. 지금까지 검증자의 모든 단계는 실제로 증명자가 주장하는 가치에 의존하지 않았습니다. 확인하는 방법은 다음과 같습니다. 계산 지점으로 표시한 "열 부분"의 텐서 곱을 사용합니다.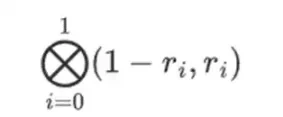

우리의 경우 r = { 1, 2, 3, 4 }이므로 선택한 열의 절반이 { 1, 2 }) 이는 다음과 같습니다.

이제 우리는 이 선형 조합 t를 취합니다:

이는 다항식을 직접 푸는 것과 같습니다.

위의 내용은 간단한 Binius 프로토콜에 대한 완전한 설명에 매우 가깝습니다. 여기에는 이미 몇 가지 흥미로운 이점이 있습니다. 예를 들어 데이터가 행과 열로 분리되어 있으므로 크기가 절반인 필드만 필요합니다. 그러나 이는 바이너리 컴퓨팅의 모든 이점을 달성하지 못합니다. 이를 위해서는 전체 Binius 프로토콜이 필요합니다. 하지만 먼저 이진 필드에 대해 자세히 살펴보겠습니다.

바이너리 필드

가능한 가장 작은 필드는 산술 모듈로 2입니다. 이는 너무 작아서 이에 대한 덧셈과 곱셈표를 작성할 수 있습니다.

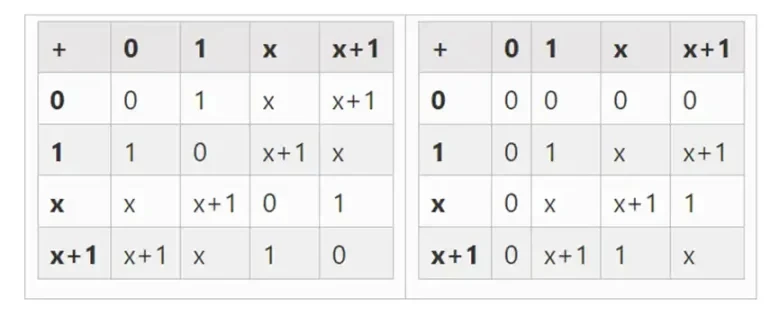
확장을 통해 더 큰 이진 필드를 얻을 수 있습니다. F 2(모듈로 2의 정수)로 시작한 다음 x 제곱 = x + 1인 x를 정의하면 다음과 같은 덧셈 및 곱셈 테이블을 얻을 수 있습니다.

이 구성을 반복함으로써 이진 필드를 임의의 큰 크기로 확장할 수 있다는 것이 밝혀졌습니다. 새 요소를 추가할 수 있지만 더 이상 요소 I를 추가할 수 없는 실수에 대한 복소수와 달리 I(쿼터니언은 존재하지만 수학적으로 이상합니다. 예: ab는 ba와 같지 않음) 유한 필드를 사용하면 새 확장을 추가할 수 있습니다. 영원히. 구체적으로 요소에 대한 정의는 다음과 같습니다.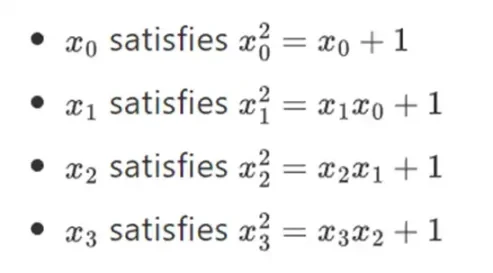

등등… 이것은 종종 타워 건설이라고 불립니다. 왜냐하면 각각의 연속적인 확장은 타워에 새로운 레이어를 추가하는 것으로 생각할 수 있기 때문입니다. 이는 임의 크기의 이진 필드를 구성하는 유일한 방법은 아니지만 Binius가 활용하는 몇 가지 고유한 이점이 있습니다.

우리는 이러한 숫자를 비트 목록으로 표현할 수 있습니다. 예를 들어, 1100101010001111입니다. 첫 번째 비트는 1의 배수를 나타내고, 두 번째 비트는 x0의 배수를 나타내며, x1, x1*x0, x2, x2*x0 등의 비트는 x1의 배수를 나타냅니다. 이 인코딩은 분해할 수 있기 때문에 좋습니다.

이것은 상대적으로 흔하지 않은 표기법이지만 저는 이진 필드 요소를 정수로 표현하고 오른쪽에 더 효율적인 비트를 사용하는 것을 좋아합니다. 즉, 1 = 1, x0 = 01 = 2, 1+x0 = 11 = 3, 1+x0+x2 = 11001000 = 19 등입니다. 이 표현에서는 61779입니다.

이진 필드의 덧셈은 단지 XOR입니다(그리고 뺄셈도 마찬가지입니다). 이는 모든 x에 대해 x+x = 0을 의미합니다. 두 요소 x*y를 함께 곱하려면 매우 간단한 재귀 알고리즘이 있습니다. 즉, 각 숫자를 반으로 나누는 것입니다.

그런 다음 곱셈을 나눕니다.

마지막 부분은 단순화 규칙을 적용해야 하기 때문에 약간 까다로운 유일한 부분입니다. Karatsubas 알고리즘 및 고속 푸리에 변환과 유사하게 곱셈을 수행하는 더 효율적인 방법이 있지만 관심 있는 독자가 알아낼 수 있는 연습으로 남겨두겠습니다.

이진 필드의 나눗셈은 곱셈과 역산을 결합하여 수행됩니다. 간단하지만 느린 반전 방법은 일반화된 페르마의 작은 정리를 적용한 것입니다. 여기에서 찾을 수 있는 더 복잡하지만 더 효율적인 반전 알고리즘도 있습니다. 여기에 있는 코드를 사용하여 이진 필드의 덧셈, 곱셈, 나눗셈을 수행할 수 있습니다.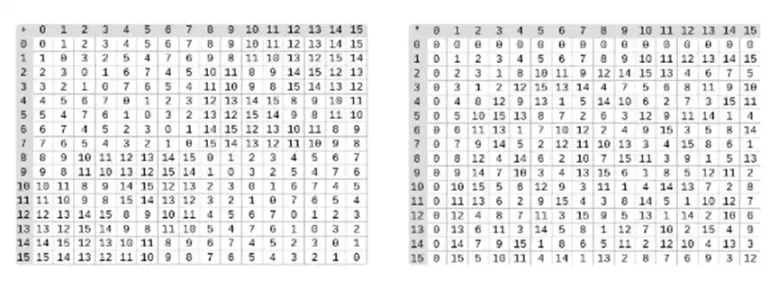

왼쪽: 4비트 이진 필드 요소에 대한 추가 테이블(즉, 1, x 0, x 1, x 0x 1만). 오른쪽: 4비트 이진 필드 요소에 대한 곱셈표.

이러한 유형의 이진 필드의 장점은 일반 정수와 모듈러 산술의 가장 좋은 부분 중 일부를 결합한다는 것입니다. 일반 정수와 마찬가지로 이진 필드 요소에는 제한이 없습니다. 원하는 만큼 커질 수 있습니다. 그러나 모듈러 산술과 마찬가지로 특정 크기 제한 내의 값에 대해 연산을 수행하면 모든 결과가 동일한 범위에 유지됩니다. 예를 들어, 42를 연속적으로 거듭제곱하면 다음과 같은 결과를 얻습니다.

255단계 후에는 42의 255 = 1제곱으로 돌아가며 양의 정수 및 모듈러 연산과 마찬가지로 일반적인 수학 법칙(a*b=b*a, a*(b+c)=)을 따릅니다. a*b+a*c, 그리고 심지어 이상한 새로운 법칙도 있습니다.

마지막으로 이진 필드는 비트를 조작하는 데 편리합니다. 2k에 맞는 숫자로 수학을 수행하면 모든 출력도 2k 비트에 맞습니다. 이것은 어색함을 방지합니다. Ethereum EIP-4844에서 blob의 개별 블록은 모듈로 52435875175126190479447740508185965837690552500527637822603658699938581184513이어야 합니다. 따라서 바이너리 데이터를 인코딩하려면 일부 공간을 버리고 애플리케이션 계층에서 추가 검사를 수행해야 합니다. 각 요소에 저장된 값은 2248보다 작습니다. 이는 또한 CPU와 이론적으로 최적의 FPGA 및 ASIC 설계 모두에서 바이너리 필드 작업이 컴퓨터에서 매우 빠르다는 것을 의미합니다.

이는 모두 위에서 했던 것처럼 Reed-Solomon 인코딩을 수행할 수 있다는 것을 의미합니다. 예에서 본 것처럼 정수 폭발을 완전히 피하는 방식과 컴퓨터가 능숙하게 수행할 수 있는 매우 기본적인 방식의 계산 방식입니다. 이진 필드의 분할 속성(1100101010001111 = 11001010 + 10001111*x 3 을 수행한 다음 필요에 따라 분할하는 방법)도 많은 유연성을 허용하는 데 중요합니다.

비니우스를 완료하세요

보다 여기 프로토콜의 Python 구현을 위해.

이제 (i) 바이너리 필드 작업 및 (ii) 단일 비트 커밋에 "단순 Binius"를 적용하는 "전체 Binius"로 이동할 수 있습니다. 이 프로토콜은 비트 행렬을 보는 서로 다른 방식 사이를 앞뒤로 전환하기 때문에 이해하기 어렵습니다. 암호화 프로토콜을 이해하는 데 보통 걸리는 것보다 그것을 이해하는 데 확실히 더 오랜 시간이 걸렸습니다. 그러나 일단 이진 필드를 이해하고 나면 Binius가 의존하는 "더 어려운 수학"이 존재하지 않는다는 좋은 소식이 있습니다. 이것은 점점 더 깊어지는 대수 기하학 토끼 구멍이 있는 타원 곡선 쌍이 아닙니다. 여기에는 바이너리 필드만 있습니다.

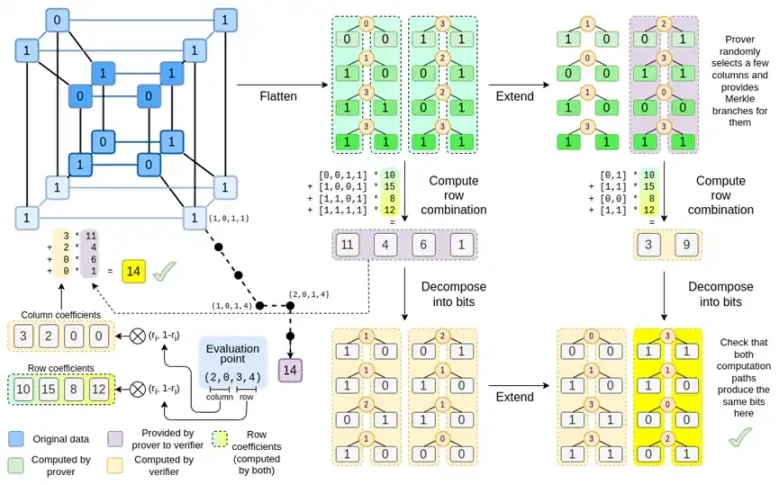
전체 차트를 다시 살펴보겠습니다.

이제 대부분의 구성요소에 익숙해졌을 것입니다. 하이퍼큐브를 그리드로 평면화하는 아이디어, 평가 포인트의 텐서 곱으로 행과 열 조합을 계산하는 아이디어, 리드-솔로몬 확장 간의 동등성을 확인한 다음 행 조합을 계산하고 행 조합을 계산한 다음 리드-솔로몬 확장을 계산하는 아이디어 모두 일반 Binius로 구현되었습니다.

Complete Binius의 새로운 기능은 무엇입니까? 기본적으로 세 가지:

• 하이퍼큐브와 정사각형의 개별 값은 비트(0 또는 1)여야 합니다.

• 확장 프로세스는 비트를 열로 그룹화하고 일시적으로 더 큰 필드의 요소라고 가정하여 비트를 더 많은 비트로 확장합니다.

• 행 조합 단계 후에는 확장을 다시 비트로 변환하는 요소별 비트 분해 단계가 있습니다.

두 경우를 차례로 논의해 보세요. 첫째, 새로운 확장 절차입니다. 리드 솔로몬 코드에는 근본적인 한계가 있습니다. n을 k*n으로 확장하려면 좌표로 사용할 수 있는 k*n 다른 값을 사용하여 필드에서 작업해야 합니다. F 2(일명 비트)로는 그렇게 할 수 없습니다. 그래서 우리가 하는 일은 F 2 의 인접한 요소를 함께 묶어 더 큰 값을 형성하는 것입니다. 여기 예에서는 한 번에 2비트를 {0, 1, 2, 3} 요소에 압축합니다. 확장에는 계산 포인트가 4개만 있으므로 이 정도면 충분합니다. 실제 증명에서는 한 번에 16비트씩 돌아갈 수도 있습니다. 그런 다음 이러한 압축된 값에 대해 Reed-Solomon 코드를 실행하고 이를 다시 비트로 압축 해제합니다.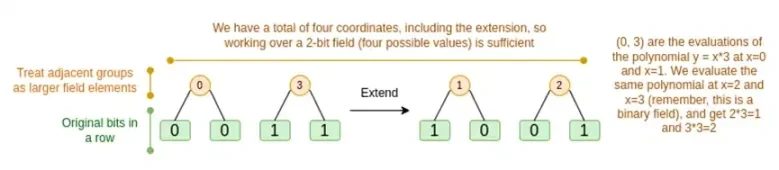

이제 행 조합입니다. 임의 지점 검사를 암호학적으로 안전하게 평가하려면 상당히 큰 공간(하이퍼큐브 자체보다 훨씬 큼)에서 해당 지점을 샘플링해야 합니다. 따라서 하이퍼큐브 내부의 점이 비트인 반면, 하이퍼큐브 외부의 계산된 값은 훨씬 더 커집니다. 위의 예에서 행 조합은 결국 [11, 4, 6, 1]이 됩니다.

이는 문제를 야기합니다. 비트를 더 큰 값으로 그룹화한 다음 해당 값에 대해 리드-솔로몬 확장을 수행하는 방법을 알고 있지만 더 큰 값 쌍에 대해 동일한 작업을 어떻게 수행합니까?

Binius 트릭은 비트 단위로 수행하는 것입니다. 각 값의 단일 비트를 살펴본 다음(예: 11로 레이블을 붙인 항목은 [1, 1, 0, 1]) 행 단위로 확장합니다. 즉, 각 요소의 1번째 행, x0 행, x1 행, x0x1 행 등으로 확장합니다. (글쎄, 우리의 장난감 예에서는 여기서 멈췄지만 실제로는 구현 시 최대 128개 행까지 가능합니다(마지막 행은 x6*…*x0).

검토:

• 하이퍼큐브의 비트를 그리드로 변환합니다.

• 그런 다음 각 행의 인접한 비트 그룹을 더 큰 필드의 요소로 처리하고 이에 대해 산술 연산을 수행하여 Reed-Solomon이 행을 확장합니다.

• 그런 다음 각 비트 열의 행 조합을 취하고 각 행의 비트 열을 출력으로 얻습니다(4 x 4보다 큰 정사각형의 경우 훨씬 작음).

• 그런 다음 출력을 행렬로 간주하고 해당 비트를 행으로 간주합니다.

왜 이런 일이 발생합니까? 일반 수학에서 숫자를 비트 단위로 쪼개기 시작하면 어떤 순서로든 선형 연산을 수행하고 동일한 결과를 얻는 (일반적인) 능력이 무너집니다. 예를 들어 숫자 345에 8을 곱하고 3을 곱하면 8280이 되고, 이 두 연산을 역으로 하면 역시 8280이 됩니다. 그런데 비트 슬라이싱 연산을 삽입하면 두 단계 사이에서 세분화됩니다. 8x, 3x를 수행하면 다음과 같은 결과를 얻습니다.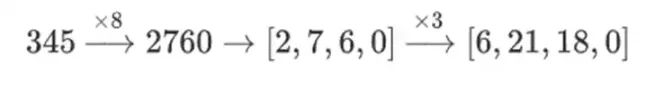

하지만 3배, 8배를 하면 다음과 같은 결과를 얻을 수 있습니다.

그러나 타워 구조로 구축된 이진 필드에서는 이 접근 방식이 작동합니다. 그 이유는 분리 가능성 때문입니다. 큰 값에 작은 값을 곱하면 각 세그먼트에서 발생하는 내용이 각 세그먼트에 유지됩니다. 1100101010001111에 11을 곱하면 1100101010001111의 첫 번째 분해와 같습니다.

그런 다음 각 구성요소에 11을 곱합니다.

함께 모아서

일반적으로 영지식 증명 시스템은 동시에 기본 평가에 대한 설명을 나타내는 다항식에 대한 설명을 작성하여 작동합니다. 피보나치 예에서 본 것처럼 F(X+ 2)-F(X+ 1)-F( X) = Z(X)*H(X) 피보나치 계산의 모든 단계를 확인하는 동안. 우리는 임의의 지점에서 평가를 증명하여 다항식에 대한 설명을 확인합니다. 이 무작위 점 확인은 전체 다항식 확인을 나타냅니다. 다항식 방정식이 일치하지 않으면 특정 무작위 좌표에서 일치할 가능성이 적습니다.

실제로 비효율성의 주요 원인 중 하나는 실제 프로그램에서 우리가 다루는 대부분의 숫자(for 루프의 인덱스, True/False 값, 카운터 등)가 작다는 것입니다. 그러나 Merkle 증명 기반 검사를 안전하게 만드는 데 필요한 중복성을 제공하기 위해 Reed-Solomon 인코딩으로 데이터를 확장하면 원래 값이 작더라도 대부분의 추가 값이 필드의 전체 크기를 차지하게 됩니다.

이 문제를 해결하기 위해 이 필드를 가능한 한 작게 만들고 싶습니다. Plonky 2는 256비트 숫자에서 64비트 숫자로, Plonky 3에서는 이를 31비트로 더 낮췄습니다. 그러나 그것조차 최적은 아니다. 이진 필드를 사용하면 단일 비트를 처리할 수 있습니다. 이로 인해 인코딩이 조밀해집니다. 실제 기본 데이터에 n 비트가 있는 경우 인코딩은 n 비트를 가지며 확장은 추가 오버헤드 없이 8*n 비트를 갖게 됩니다.

이제 이 차트를 세 번째로 살펴보겠습니다.

Binius에서는 다중선형 다항식인 하이퍼큐브 P(x0, x1,…xk)에 대해 작업합니다. 여기서 단일 평가는 P(0, 0, 0, 0), P(0, 0, 0, 1)부터 P( 1, 1, 1, 1), 우리가 관심 있는 데이터를 보관하세요. 특정 지점에서의 계산을 증명하기 위해 동일한 데이터를 정사각형으로 재해석합니다. 그런 다음 Reed-Solomon 인코딩을 사용하여 각 행을 확장하여 무작위 Merkle 분기 쿼리에 대한 보안에 필요한 데이터 중복성을 제공합니다. 그런 다음 행의 무작위 선형 조합을 계산하여 새로운 결합된 행에 우리가 관심 있는 계산 값이 실제로 포함되도록 계수를 설계합니다. 새로 생성된 이 행(128비트 행으로 재해석됨)과 Merkle 분기가 있는 무작위로 선택된 일부 열이 검증자에게 전달됩니다.

그런 다음 검증자는 확장된 행 조합(또는 더 정확하게는 확장된 열)과 확장된 행 조합을 수행하고 두 가지가 일치하는지 확인합니다. 그런 다음 열 조합을 계산하고 증명자가 주장한 값을 반환하는지 확인합니다. 이것이 우리의 증명 시스템(또는 더 정확하게는 증명 시스템의 핵심 구성 요소인 다항식 확약 체계)입니다.

아직 다루지 않은 내용은 무엇인가요?

• 실제로 유효성 검사기를 계산적으로 효율적으로 만들려면 행을 확장하는 효율적인 알고리즘이 필요합니다. 여기에 설명된 대로 이진 필드에 고속 푸리에 변환을 사용합니다(비록 이 게시물에서는 재귀 확장을 기반으로 하지 않는 덜 효율적인 구성을 사용하므로 정확한 구현은 다를 수 있습니다).

• 산술적으로. 일변량 다항식은 F(X+2)-F(X+1)-F(X) = Z(X)*H(X)와 같은 작업을 수행하여 계산의 인접 단계를 연결할 수 있으므로 편리합니다. 하이퍼큐브에서 다음 단계는 X+1보다 훨씬 덜 잘 설명됩니다. X+k, k의 거듭제곱을 수행할 수 있지만 이러한 점프 동작은 Binius의 주요 장점 중 많은 부분을 희생합니다. Binius 논문에서는 솔루션을 설명합니다. 섹션 4.3 참조) 그러나 이것은 그 자체로 깊은 토끼굴입니다.

• 특정 값 확인을 안전하게 수행하는 방법. 피보나치 예에서는 주요 경계 조건, 즉 F(0)=F(1)=1 및 F(100) 값을 확인해야 했습니다. 그러나 원래 Binius의 경우 알려진 계산 지점에서 검사를 수행하는 것은 안전하지 않습니다. 소위 합계 검사 프로토콜을 사용하여 알려진 계산 검사를 알려지지 않은 계산 검사로 변환하는 매우 간단한 방법이 있습니다. 하지만 여기서는 다루지 않겠습니다.

• 최근 널리 사용되는 또 다른 기술인 조회 프로토콜은 매우 효율적인 증명 시스템을 만드는 데 사용됩니다. Binius는 많은 애플리케이션에 대한 조회 프로토콜과 함께 사용할 수 있습니다.

• 제곱근 검증 시간을 초과합니다. 제곱근은 비용이 많이 듭니다. 2^32비트의 Binius 증명은 길이가 약 11MB입니다. 다른 증명 시스템을 사용하여 Binius 증명을 만들어 이를 보완할 수 있으며, 더 작은 증명 크기로 Binius 증명의 효율성을 제공합니다. 또 다른 옵션은 (일반 FRI와 마찬가지로) 다중 로그 크기 증명을 생성하는 보다 복잡한 FRI-Binius 프로토콜입니다.

• Binius가 SNARK 친화성에 어떻게 영향을 미치는지. 기본 요약은 Binius를 사용하면 더 이상 계산을 산술 친화적으로 만드는 데 신경 쓸 필요가 없다는 것입니다. 일반 해싱은 더 이상 기존 산술 해싱, 모듈로 2의 32제곱 또는 모듈로 2의 제곱 곱셈보다 더 효율적이지 않습니다. 256은 더 이상 모듈로 2의 곱셈만큼 고통스럽지 않습니다. 그러나 이것은 복잡한 주제입니다. 모든 것이 바이너리로 완료되면 많은 것들이 변합니다.

앞으로 몇 달 안에 바이너리 필드 기반 증명 기술이 더 많이 개선될 것으로 기대합니다.

이 기사는 인터넷에서 가져온 것입니다: Vitalik: Binius, 이진 필드에 대한 효율적인 증명

관련 항목: BNB 코인은 회복 징후를 보여줍니다: 새해 최고가 기록

간단히 말해서 BNB 가격은 $550에서 $593 저항을 돌파하는 데 1인치 더 가까워졌습니다. 가격 지표는 8% 상승을 뒷받침하는 강세 모멘텀을 되찾았습니다. 4.03의 샤프 비율은 새로운 투자자가 교환 토큰을 선택하도록 유도할 가능성이 높습니다. 3월은 BNB 코인에 유리한 달이었습니다. 암호화폐는 조정을 경험하기 전 단 며칠 만에 올해 두 번의 새로운 최고치를 달성했습니다. 거의 2주간의 회복 기간을 거친 후 BNB 코인은 2024년에 새로운 최고치에 도달할 가능성이 있는 조짐을 보이고 있습니다. 그러나 그러한 이정표가 달성 가능한가? BNB는 유망해 보입니다. $550 지원 수준에서 반등한 후, 이 분석 당시 BNB 코인의 가치는 $581로 상승했습니다. 이러한 개선은 알트코인의 위험 수익 프로필의 회복을 반영합니다.