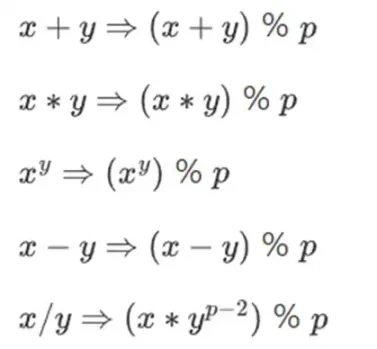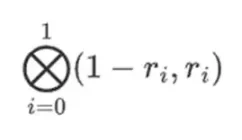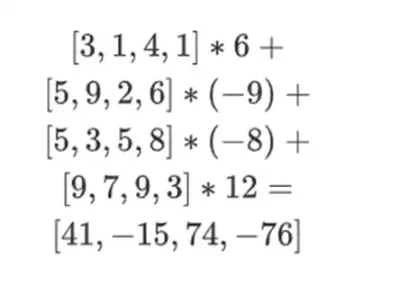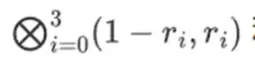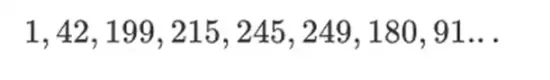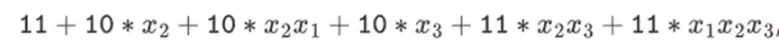ヴィタリック：ビニウス、二進体に対する効率的な証明

オリジナル記事: Vitalik Buterin

原文翻訳: Kate、MarsBit

この投稿は、2019 年当時の暗号化、特に SNARK と STARK に一般的な知識を持つ読者を主な対象としています。そうでない場合は、まずそれらを読むことをお勧めします。フィードバックとコメントを寄せてくださった Justin Drake、Jim Posen、Benjamin Diamond、Radi Cojbasic に特に感謝します。

過去 2 年間で、STARK は、非常に複雑なステートメント (たとえば、Ethereum ブロックが有効であることの証明) の簡単に検証可能な暗号証明を効率的に作成するための重要かつかけがえのないテクノロジーになりました。その主な理由の 1 つは、フィールド サイズが小さいことです。楕円曲線に基づく SNARK では、十分なセキュリティを確保するために 256 ビットの整数で作業する必要がありますが、STARK では、より効率的にはるかに小さいフィールド サイズを使用できます。最初は Goldilocks フィールド (64 ビット整数)、次に Mersenne 31 と BabyBear (どちらも 31 ビット) です。これらの効率性の向上により、Goldilocks を使用する Plonky 2 は、多くの種類の計算の証明において、以前のバージョンよりも数百倍高速です。

当然の疑問は、この傾向を論理的に結論づけて、0 と 1 を直接操作することでより高速に実行される証明システムを構築できるかどうかです。これはまさに Binius が試みていることであり、3 年前の SNARK や STARK とはまったく異なるいくつかの数学的トリックを使用しています。この記事では、小さなフィールドによって証明生成がより効率的になるのはなぜか、バイナリ フィールドが特に強力なのはなぜか、そして Binius がバイナリ フィールドでの証明を非常に効率的にするために使用するトリックについて説明します。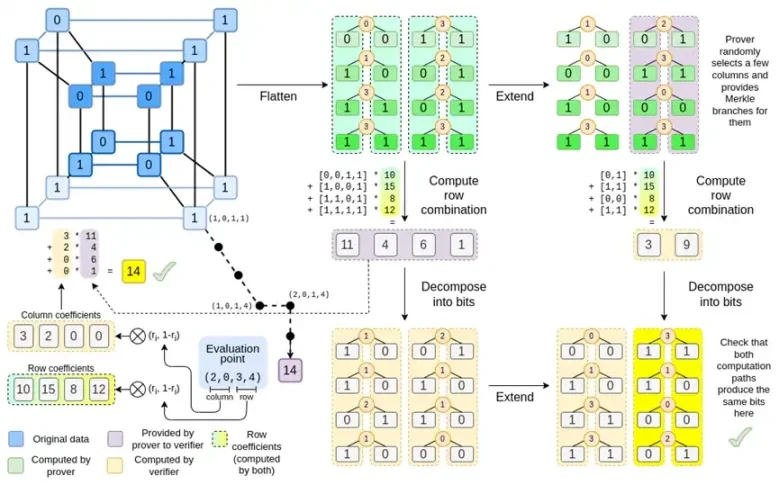

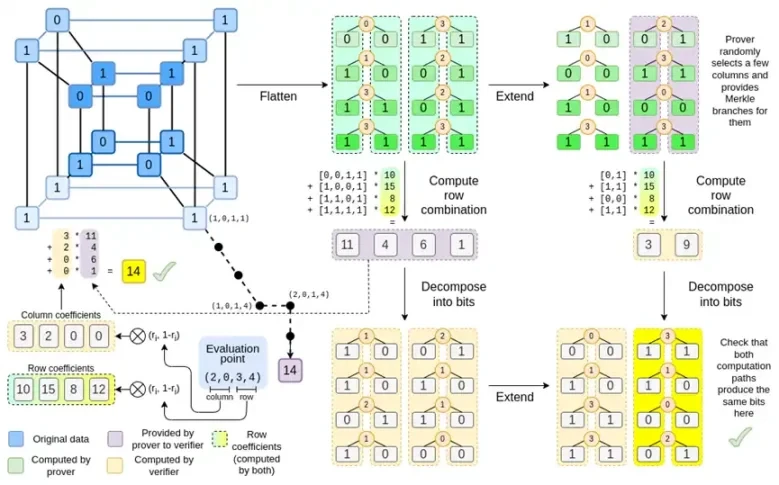
Binius さん、この投稿を読み終える頃には、この図のすべての部分を理解できるはずです。

復習: 有限体

暗号証明システムの主要なタスクの 1 つは、数値を小さく保ちながら大量のデータを処理することです。大規模なプログラムに関するステートメントを、いくつかの数値を含む数式に圧縮できたとしても、その数値が元のプログラムと同じ大きさであれば、何も得られません。

数値を小さく保ちながら複雑な計算を行うために、暗号学者はしばしばモジュラー演算を使用します。素数を p で割ったものを選択します。% 演算子は剰余を取ることを意味します。15% 7 = 1、53% 10 = 3 などです。(答えは常に非負であることに注意してください。たとえば、-1% 10 = 9 です)

モジュラー演算は、時間の加算と減算の文脈で見たことがあるかもしれません (例: 9 時 4 分後は何時ですか?)。ただし、ここでは、数を法として加算と減算するだけでなく、乗算、除算、指数を取ることもできます。

再定義します:

上記の規則はすべて自己矛盾がありません。たとえば、p = 7 の場合、次のようになります。

5 + 3 = 1 (8% 7 = 1 なので)

1-3 = 5 (-2% 7 = 5 なので)

2* 5 = 3

3/5 = 2

このような構造のより一般的な用語は有限体です。有限体とは、通常の算術法則に従う数学的構造ですが、可能な値の数は有限であるため、各値は固定サイズで表すことができます。

モジュラー演算 (または素体) は最も一般的なタイプの有限体ですが、拡大体という別のタイプもあります。拡大体の 1 つを見たことがあるかもしれません。それは複素数です。新しい要素を想像して i とラベル付けし、それを使って計算を行います。(3i+2)*(2i+4)=6i*i+12i+4i+8=16i+2。素体の拡大についても同様に行うことができます。より小さな体を扱い始めると、素体の拡大はセキュリティ上ますます重要になり、バイナリ体 (Binius で使用) は実用的なユーティリティを実現するために拡大に完全に依存します。

レビュー: 算術化

SNARK と STARK がコンピュータ プログラムを証明する方法は、算術演算です。証明したいプログラムに関するステートメントを取得し、それを多項式を含む数式に変換します。数式の有効な解は、プログラムの有効な実行に対応します。

簡単な例として、100 番目のフィボナッチ数を計算し、それが何であるかを証明したいとします。フィボナッチ数列をエンコードする多項式 F を作成します。つまり、F(0)=F(1)=1、F(2)=2、F(3)=3、F(4)=5 のように 100 ステップ続きます。証明する必要がある条件は、範囲 x={0, 1…98} 全体にわたって F(x+2)=F(x)+F(x+1) であることです。商を示すことで納得していただけます。

ここで、Z(x) = (x-0) * (x-1) * …(x-98) です。 F と H がこの式を満たすと仮定すると、F は範囲内で F(x+ 2)-F(x+ 1)-F(x) を満たす必要があります。 さらに、F について F(0)=F(1)=1 であることを確認すると、F(100) は実際には 100 番目のフィボナッチ数になります。

もっと複雑なことを証明したい場合は、単純な関係 F(x+2) = F(x) + F(x+1) を、基本的に F(x+1) が状態 F(x) で仮想マシンを初期化した出力であるというより複雑な方程式に置き換え、1 つの計算ステップを実行します。また、より多くのステップに対応するために、100 という数字を 100000000 などのより大きな数字に置き換えることもできます。

すべての SNARK と STARK は、多項式 (および場合によってはベクトルと行列) 上の単純な方程式を使用して、個々の値間の多数の関係を表すというアイデアに基づいています。すべてのアルゴリズムが、上記のように隣接する計算ステップ間の同等性をチェックするわけではありません。たとえば、PLONK はそうしませんし、R1CS もそうしません。ただし、最も効果的なチェックの多くはそうします。これは、同じチェック (または同じいくつかのチェック) を何度も実行することでオーバーヘッドを最小限に抑えることが容易になるためです。

Plonky 2: 256 ビットの SNARK と STARK から 64 ビットの STARK のみへ

5 年前、ゼロ知識証明のさまざまなタイプを合理的にまとめると次のようになります。証明には、(楕円曲線ベースの) SNARK と (ハッシュベースの) STARK の 2 種類があります。技術的には、STARK は SNARK の一種ですが、実際には、楕円曲線ベースのバリアントを指す場合は「SNARK」を使用し、ハッシュベースの構造を指す場合は「STARK」を使用するのが一般的です。SNARK は小さいため、非常に迅速に検証し、簡単にオンチェーンにインストールできます。STARK は大きいですが、信頼できるセットアップを必要とせず、量子耐性があります。

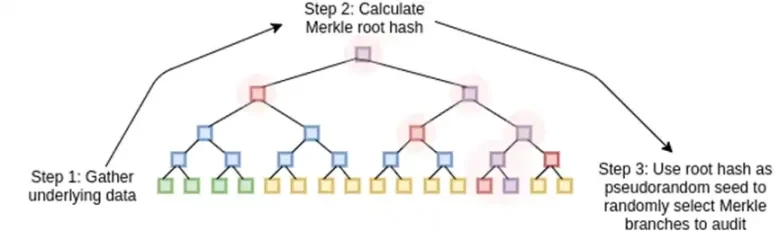
STARK は、データを多項式として扱い、その多項式の計算を行い、拡張データの Merkle 根を「多項式コミットメント」として使用することで機能します。

ここで重要な歴史は、楕円曲線ベースの SNARK が最初に広く使用されたことです。STARK は、FRI のおかげで 2018 年頃まで十分に効率的ではありませんでしたが、その時点で Zcash は 1 年以上稼働していました。楕円曲線ベースの SNARK には重要な制限があります。楕円曲線ベースの SNARK を使用する場合、これらの式の演算は、楕円曲線上の点の数を法として実行する必要があります。これは大きな数値で、通常は 2 の 256 乗に近い値です。たとえば、bn128 曲線の場合は 21888242871839275222246405745257275088548364400416034343698204186575808495617 です。ただし、実際のコンピューティングでは小さな数値が使用されます。お気に入りの言語の実際のプログラムについて考えてみると、使用されるもののほとんどは、カウンター、for ループ内のインデックス、プログラム内の位置、True または False を表す単一ビット、およびほとんどの場合数桁の長さのその他のものです。

元のデータが小さな数値で構成されていても、証明プロセスでは商、展開、ランダム線形結合、およびその他のデータ変換を計算する必要があり、その結果、平均してフィールドのフルサイズと同じかそれ以上の数のオブジェクトが生成されます。これにより、重要な非効率性が生じます。n 個の小さな値での計算を証明するには、n 個のはるかに大きな値でさらに多くの計算を実行する必要があります。当初、STARK は 256 ビット フィールドを使用する SNARK の習慣を継承していたため、同じ非効率性の問題を抱えていました。

多項式評価のリード・ソロモン展開。元の値は小さいが、追加の値はフィールドのフルサイズ（この場合は 2^31 – 1）まで拡張される。

2022年にPlonky 2がリリースされました。Plonky 2の主な革新は、より小さな素数を法とする演算を行うことです。2の64乗-2の32乗+1=18446744067414584321。これで、各加算または乗算は常にCPU上のいくつかの命令で実行でき、すべてのデータを一緒にハッシュする速度は以前よりも4倍高速になりました。ただし、問題があります。この方法はSTARKにしか機能しません。SNARKを使用しようとすると、楕円曲線はそのような小さな楕円曲線に対して安全ではなくなります。

セキュリティを確保するために、Plonky 2 では拡張体も導入する必要があります。算術方程式をチェックするための重要な手法は、ランダム ポイント サンプリングです。H(x) * Z(x) が F(x+ 2)-F(x+ 1)-F(x) に等しいかどうかをチェックする場合、座標 r をランダムに選択し、H(r)、Z(r)、F(r)、F(r+ 1)、F(r+ 2) を証明するための多項式コミットメントを提供してから、H(r) * Z(r) が F(r+ 2)-F(r+ 1)- F(r) に等しいかどうかを確認します。攻撃者が事前に座標を推測できる場合、攻撃者は証明システムを欺くことができます。これが、証明システムがランダムでなければならない理由です。しかし、これはまた、攻撃者がランダムに推測できないほど十分に大きなセットから座標をサンプリングする必要があることも意味します。係数が 2 の 256 乗に近い場合、これは明らかに当てはまります。ただし、係数 2^64 – 2^32 + 1 の場合、まだその値に達しておらず、2^31 – 1 まで下がった場合は明らかに当てはまりません。攻撃者が幸運に恵まれるまで 20 億回証明を偽造しようとすることは十分に可能です。

これを防ぐために、拡張フィールドから r をサンプリングします。これにより、たとえば、y^3 = 5 となる y を定義し、1、y、y^2 の組み合わせを取ることができます。これにより、座標の総数は約 2^93 になります。証明者が計算する多項式のほとんどは、この拡張フィールドには入りません。これらは 2^31-1 を法とする整数にすぎないため、小さなフィールドを使用することで、依然としてすべての効率が得られます。ただし、ランダム ポイント チェックと FRI 計算は、必要なセキュリティを得るために、このより大きなフィールドにまで到達します。

小さな素数から2進数まで

コンピュータは、大きな数を 0 と 1 のシーケンスとして表し、それらのビットの上に回路を構築して加算や乗算などの演算を行うことで算術演算を行います。コンピュータは、16 ビット、32 ビット、および 64 ビットの整数に特に最適化されています。たとえば、2^64 – 2^32 + 1 と 2^31 – 1 は、これらの境界内に収まるだけでなく、これらの境界内にうまく収まるという理由でも選択されました。2^64 – 2^32 + 1 を法とする乗算は、通常の 32 ビット乗算を行い、出力をビット単位でシフトして数か所にコピーすることで実行できます。この記事では、いくつかのトリックをわかりやすく説明しています。

しかし、もっと良い方法は、計算をバイナリで直接行うことです。1 + 1 をあるビットから次のビットに加算する際の繰り越しを気にせずに、加算を XOR だけで済ませることができたらどうでしょう。同様に、乗算もより並列化できたらどうでしょう。これらの利点はすべて、1 ビットで真偽値を表現できることに基づいています。

バイナリ計算を直接行うことで得られるこれらの利点を、まさに Binius が実現しようとしています。Binius チームは、zkSummit でのプレゼンテーションで効率性の向上を実証しました。

ほぼ同じサイズであるにもかかわらず、32 ビットのバイナリ フィールドの操作では、31 ビットのメルセンヌ フィールドの操作よりも 5 倍少ない計算リソースが必要です。

一変数多項式から超立方体へ

この推論を信じて、すべてをビット (0 と 1) で実行したいとします。10 億ビットを 1 つの多項式で表現するにはどうすればよいでしょうか。

ここで、2 つの実際的な問題に直面します。

1. 多項式が多数の値を表すためには、多項式を評価するときにこれらの値にアクセスできる必要があります。上記のフィボナッチの例では、F(0)、F(1)…F(100) となり、より大規模な計算では指数は数百万単位になります。使用するフィールドには、このサイズの数値が含まれている必要があります。

2. マークル木にコミットする値を証明するには (すべての STARK と同様に)、リード・ソロモン符号化が必要です。たとえば、悪意のある証明者が計算中に値を偽造して不正行為をしないように冗長性を使用して、値を n から 8n に拡張します。これには、十分に大きなフィールドも必要です。100 万の値を 800 万に拡張するには、多項式を評価するために 800 万の異なるポイントが必要です。

Binius の重要なアイデアは、これら 2 つの問題を別々に解決し、同じデータを 2 つの異なる方法で表現することです。まず、多項式自体です。楕円曲線ベースの SNARK、2019 年型の STARK、Plonky 2 などのシステムでは、通常、1 つの変数に対する多項式 (F(x)) を扱います。一方、Binius は Spartan プロトコルからヒントを得て、多変数多項式 (F(x 1, x 2,… xk)) を使用します。実際には、計算の軌跡全体を計算のハイパーキューブで表します。ここで、各 xi は 0 または 1 です。たとえば、フィボナッチ数列を表現する場合、それらを表現するのに十分な大きさのフィールドを使用すると、最初の 16 個の数列を次のように想像できます。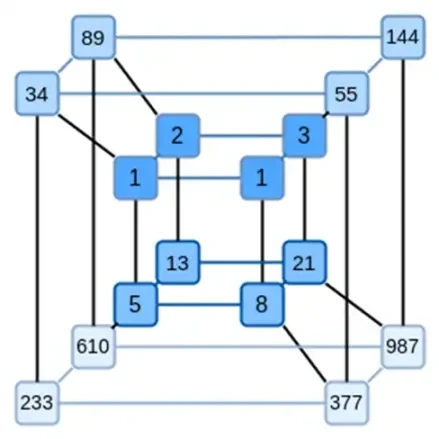

つまり、F(0,0,0,0) は 1、F(1,0,0,0) も 1、F(0,1,0,0) は 2 などとなり、最終的には F(1,1,1,1) = 987 になります。このような計算のハイパーキューブを考えると、これらの計算を生成する多変量線形 (各変数の次数 1) 多項式があります。したがって、この値のセットは多項式を表すものと考えることができます。係数を計算する必要はありません。

この例は、もちろん説明のためだけのものです。実際には、ハイパーキューブに入ることの最大の目的は、個々のビットを処理できるようにすることです。Binius 固有のフィボナッチ数を計算する方法は、高次元キューブを使用して、たとえば 16 ビットのグループごとに 1 つの数値を格納することです。これには、ビット ベースで整数の加算を実装するためのある程度の巧妙さが必要ですが、Binius の場合、それほど難しくはありません。

さて、消去コードを見てみましょう。STARK の仕組みは、n 個の値を取り、リード ソロモン拡張してより多くの値 (通常は 8n、通常は 2n から 32n の間) にし、拡張からランダムにいくつかの Merkle ブランチを選択して、何らかのチェックを実行するというものです。ハイパーキューブは各次元の長さが 2 です。したがって、直接拡張するのは現実的ではありません。16 個の値から Merkle ブランチをサンプリングするのに十分なスペースがないのです。では、どのように行うのでしょうか。ハイパーキューブが正方形であると仮定しましょう。

シンプルなビニウス – 例

見る ここ プロトコルの Python 実装用。

便宜上、通常の整数をフィールドとして使用する例を見てみましょう (実際の実装では、バイナリ フィールド要素を使用します)。まず、送信するハイパーキューブを正方形としてエンコードします。

ここで、リード・ソロモン法を使用して平方を展開します。つまり、各行を x = {0, 1, 2, 3} で評価される 3 次多項式として扱い、同じ多項式を x = {4, 5, 6, 7} で評価します。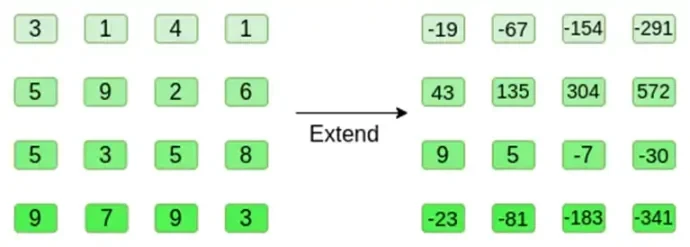

数値が非常に大きくなる可能性があることに注意してください。これが、実際の実装では通常整数ではなく有限体を使用する理由です。たとえば、11 を法とする整数を使用する場合、最初の行の展開は [3, 10, 0, 6] になります。

拡張機能を試して自分で数値を確認したい場合は、ここにある簡単なリード・ソロモン拡張機能コードを使用できます。

次に、この拡張を列として扱い、列の Merkle ツリーを作成します。Merkle ツリーのルートがコミットメントです。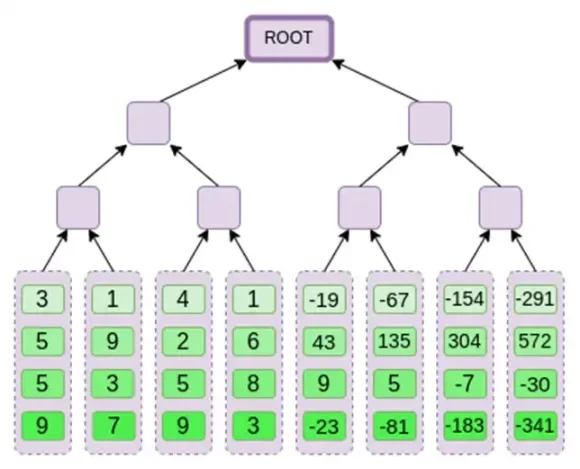

ここで、証明者がこの多項式 r = {r 0, r 1, r 2, r 3 } の計算をある時点で証明したいとします。 Binius には、他の多項式コミットメント スキームよりも弱い微妙な違いがあります。証明者は、マークル根にコミットする前に s を知ったり推測したりしてはなりません (言い換えると、r はマークル根に依存する疑似乱数値である必要があります)。これにより、このスキームはデータベース検索には役に立たなくなります (たとえば、マークル根がわかったので、今度は P(0, 0, 1, 0) を証明してください)。ただし、実際に使用するゼロ知識証明プロトコルでは、通常、データベース検索は必要ありません。必要なのは、ランダムな評価ポイントで多項式をチェックすることだけです。そのため、この制限は目的に十分役立ちます。

r = { 1, 2, 3, 4 } を選択したとします (多項式は -137 と評価されます。このコードを使用してこれを確認できます)。次に、証明に移ります。r を 2 つの部分に分割します。最初の部分 { 1, 2 } は行内の列の線形結合を表し、2 番目の部分 { 3, 4 } は行の線形結合を表します。列のテンソル積とを計算します。

行部分の場合:

これは、各セット内の値のすべての可能な積のリストを意味します。行の場合、次のようになります。

[( 1-r 2)*( 1-r 3)、( 1-r 3)、( 1-r 2)*r 3、r 2*r 3 ]

r = { 1, 2, 3, 4 } の場合（つまり r 2 = 3、r 3 = 4）：

[( 1-3)*( 1-4), 3*( 1-4),( 1-3)* 4, 3* 4 ] = [ 6, -9 -8 -12 ]

ここで、既存の行の線形結合を取って新しい行 t を計算します。つまり、次のようになります。

ここで起こっていることは部分評価と考えることができます。完全なテンソル積をすべての値の完全なベクトルで乗算すると、計算 P(1, 2, 3, 4) = -137 が得られます。ここでは、評価座標の半分だけを使用して部分テンソル積を乗算し、N 個の値のグリッドを平方根 N 個の値の 1 行に減らしました。この行を他の人に渡すと、その人は評価座標の残りの半分のテンソル積を使用して残りの計算を行うことができます。

証明者は検証者に次の新しい行 t とランダムにサンプリングされた列の Merkle 証明を提供します。この例では、証明者に最後の列のみを提供してもらいますが、実際には、十分なセキュリティを実現するために証明者は数十の列を提供する必要があります。

ここで、リード・ソロモン符号の線形性を活用します。ここで活用する重要な特性は、リード・ソロモン展開の線形結合を行うと、線形結合のリード・ソロモン展開を行うのと同じ結果が得られるという点です。この連続的な独立性は、通常、両方の操作が線形である場合に発生します。

検証者はまさにそれを行います。t を計算し、証明者が以前に計算したのと同じ列 (ただし、証明者によって提供された列のみ) の線形結合を計算し、2 つの手順で同じ答えが得られることを検証します。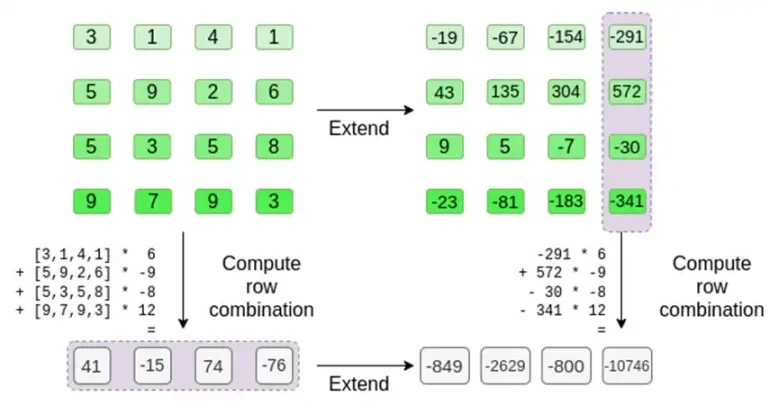

この場合、t を展開して同じ線形結合 ([6,-9,-8, 12]) を計算します。どちらも同じ答え -10746 を返します。これは、Merkle 根が誠実に (または少なくとも十分に近い形で) 構築され、t と一致していることを証明しています。少なくとも列の大部分は互いに互換性があります。

しかし、検証者が確認する必要があることがもう 1 つあります。多項式 {r 0 …r 3 } の評価を確認することです。これまでの検証者のすべてのステップは、実際には証明者が主張する値に依存していませんでした。確認方法は次のとおりです。計算ポイントとしてマークした「列部分」のテンソル積を取得します。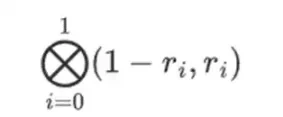

私たちの場合、r = {1, 2, 3, 4} なので、選択された列の半分は {1, 2} となり、これは次と同等です。

ここで、この線形結合 t を取ります。

これは多項式を直接解くのと同じです。

上記は、シンプルな Binius プロトコルの完全な説明に非常に近いものです。これにはすでに興味深い利点がいくつかあります。たとえば、データが行と列に分割されるため、必要なフィールドのサイズは半分になります。ただし、これではバイナリでの計算の利点を完全には得られません。そのためには、完全な Binius プロトコルが必要です。しかし、まずはバイナリ フィールドを詳しく見てみましょう。

バイナリフィールド

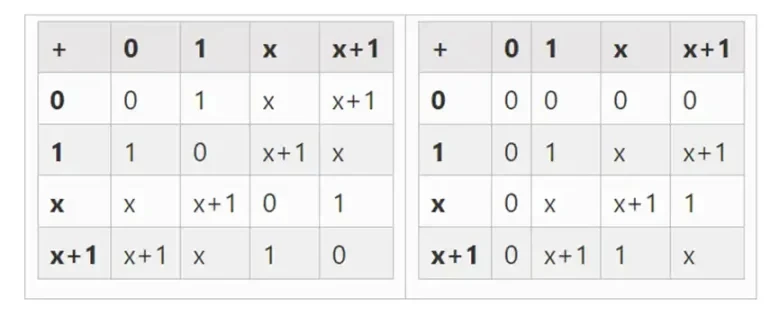
最小の可能なフィールドは 2 を法とする算術フィールドであり、これは非常に小さいため、加算表と乗算表を書くことができます。

拡張によって、より大きなバイナリ フィールドを取得できます。F 2 (2 を法とする整数) から始めて、x の 2 乗 = x + 1 となる x を定義すると、次の加算表と乗算表が得られます。

この構築を繰り返すことで、バイナリ フィールドを任意の大きさに拡張できることがわかります。実数に対する複素数では、新しい要素を追加できますが、それ以上の要素を追加することはできません (四元数は存在しますが、数学的には奇妙です。たとえば、ab は ba と等しくありません)。これとは異なり、有限フィールドでは、新しい拡張を永久に追加できます。具体的には、要素の定義は次のとおりです。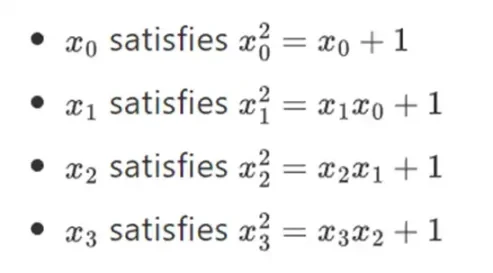

以下同様です... これは、各連続拡張がタワーに新しい層を追加すると考えられるため、タワー構築と呼ばれることがよくあります。 これは、任意のサイズのバイナリ フィールドを構築する唯一の方法ではありませんが、Binius が活用する独自の利点がいくつかあります。

これらの数字はビットのリストとして表すことができます。たとえば、1100101010001111 です。最初のビットは 1 の倍数を表し、2 番目のビットは x0 の倍数を表し、次のビットは x1 の倍数を表します: x1、x1*x0、x2、x2*x0 など。このエンコーディングは、分解できるため便利です。

これは比較的珍しい表記法ですが、私はバイナリ フィールドの要素を整数として表し、より効率的なビットを右側に配置するのが好きです。つまり、1 = 1、x0 = 01 = 2、1+x0 = 11 = 3、1+x0+x2 = 11001000 = 19 などです。この表現では、61779 になります。

2 進数フィールドでの加算は XOR です (ちなみに減算も同様です)。これは、任意の x に対して x+x = 0 であることを意味します。2 つの要素 x*y を掛け合わせるには、非常に単純な再帰アルゴリズムがあります。各数値を半分に分割します。

次に、乗算を分割します。

最後の部分だけが少しトリッキーです。単純化ルールを適用する必要があるからです。Karatsubas アルゴリズムや高速フーリエ変換に似た、より効率的な乗算方法もありますが、これは興味のある読者が考え出すための演習として残しておきます。

バイナリ フィールドでの除算は、乗算と反転を組み合わせて行います。単純ですが時間のかかる反転方法は、一般化されたフェルマーの小定理の応用です。より複雑ですが効率的な反転アルゴリズムもここにあります。ここのコードを使用して、バイナリ フィールドの加算、乗算、除算を試すことができます。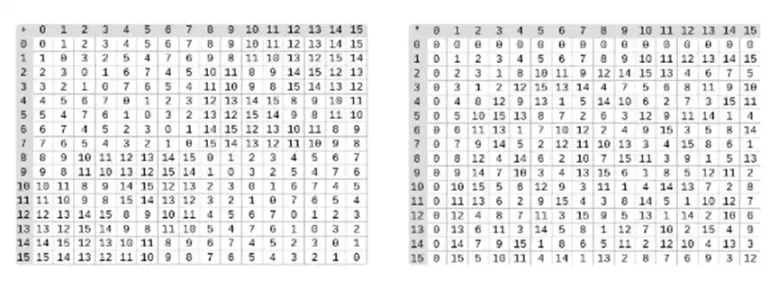

左: 4 ビットの 2 進体要素 (つまり、1、x 0、x 1、x 0x 1 のみ) の加算表。右: 4 ビットの 2 進体要素の乗算表。

このタイプのバイナリ フィールドの優れた点は、通常の整数とモジュラー演算の優れた部分を組み合わせた点です。通常の整数と同様に、バイナリ フィールドの要素は無制限です。つまり、好きなだけ大きくすることができます。ただし、モジュラー演算と同様に、特定のサイズ制限内の値に対して操作する場合、すべての結果は同じ範囲内に留まります。たとえば、42 を連続して累乗すると、次のようになります。

255 ステップ後、42 の 255 乗 = 1 に戻り、正の整数やモジュラー演算と同様に、通常の数学の法則 (a*b=b*a、a*(b+c)=a*b+a*c) に従い、さらに奇妙な新しい法則もいくつかあります。

最後に、バイナリ フィールドはビットの操作に便利です。2k に収まる数値で計算を行うと、すべての出力も 2k ビットに収まります。これにより、不自然さが回避されます。Ethereum の EIP-4844 では、blob の個々のブロックは 52435875175126190479447740508185965837690552500527637822603658699938581184513 を法とする数値でなければならないため、バイナリ データをエンコードするには、いくらかのスペースを捨て、アプリケーション レイヤーで各要素に格納されている値が 2248 未満であることを確認するための追加チェックを実行する必要があります。これは、バイナリ フィールド操作がコンピューター (CPU と理論的に最適な FPGA および ASIC 設計の両方) 上で超高速であることも意味します。

これは、上記の例で見たように整数爆発を完全に回避する方法で、非常にネイティブな方法で、コンピューターが得意とする種類の計算で、リードソロモン符号化を実行できることを意味します。バイナリフィールドの分割プロパティ、つまり 1100101010001111 = 11001010 + 10001111*x 3 を実行し、必要に応じて分割する方法も、多くの柔軟性を実現するために重要です。

ビニウスを完了する

見る ここ プロトコルの Python 実装用。

ここで、「完全 Binius」に進むことができます。これは、「単純 Binius」を (i) バイナリ フィールドで動作し、(ii) 単一ビットをコミットできるように適応させます。このプロトコルは、ビットの行列のさまざまな見方を切り替えるため、理解するのが困難です。暗号プロトコルを理解するのにかかる時間よりも、理解するのに確かに時間がかかりました。しかし、バイナリ フィールドを理解すれば、Binius が依存する「より難しい数学」は存在しないという朗報があります。これは、ますます深く潜っていくべき代数幾何学のウサギの穴がある楕円曲線のペアリングではありません。ここでは、バイナリ フィールドだけがあります。

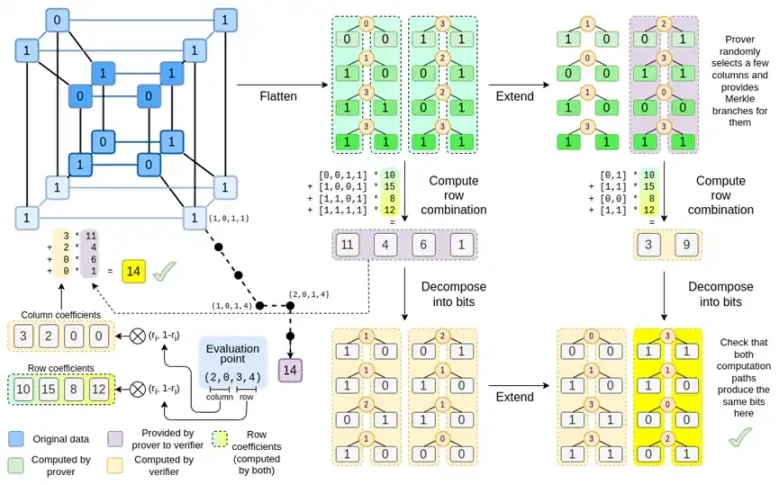
もう一度チャート全体を見てみましょう。

ここまでで、ほとんどのコンポーネントについて理解できたはずです。ハイパーキューブをグリッドに平坦化するアイデア、行と列の組み合わせを評価ポイントのテンソル積として計算するアイデア、リード・ソロモン展開を行ってから行の組み合わせを計算することと、行の組み合わせを計算してからリード・ソロモン展開を行うことの等価性を確認するというアイデアは、すべてプレーンな Binius に実装されています。

Complete Binius の新機能は? 基本的には次の 3 つです。

• ハイパーキューブと正方形の個々の値はビット (0 または 1) である必要があります。

• 拡張プロセスでは、ビットを列にグループ化し、一時的にそれらをより大きなフィールドの要素であると想定することで、ビットをさらに多くのビットに拡張します。

• 行結合ステップの後には、拡張をビットに戻す要素ごとのビット分解ステップがあります。

では、両方のケースについて順に説明します。まず、新しい拡張手順です。リード・ソロモン符号には基本的な制限があり、n を k*n に拡張する場合、座標として使用できる k*n の異なる値を持つフィールドで作業する必要があります。F 2 (ビット) では、それを行うことはできません。そのため、F 2 の隣接する要素をまとめてパックして、より大きな値を形成します。この例では、一度に 2 ビットを要素 {0、1、2、3} にパックしますが、拡張には 4 つの計算ポイントしかないため、これで十分です。実際の証明では、一度に 16 ビット戻る場合があります。次に、これらのパックされた値に対してリード・ソロモン符号を実行し、再びビットにアンパックします。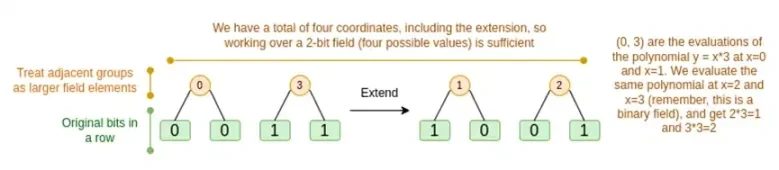

さて、行の組み合わせです。ランダムなポイントでの評価チェックを暗号的に安全にするには、そのポイントをかなり大きな空間 (ハイパーキューブ自体よりもはるかに大きい) からサンプリングする必要があります。したがって、ハイパーキューブ内のポイントはビットですが、ハイパーキューブの外側で計算された値ははるかに大きくなります。上記の例では、行の組み合わせは [11, 4, 6, 1] になります。

これによって問題が発生します。ビットを大きな値にグループ化し、その値に対してリード・ソロモン展開を実行する方法はわかっていますが、より大きな値のペアに対して同じことを実行するにはどうすればよいでしょうか。

Binius のトリックは、ビットごとに実行することです。各値の 1 ビット (たとえば、11 とラベル付けしたものは [1, 1, 0, 1]) を見て、行ごとに展開します。つまり、各要素の 1 行を展開し、次に x0 行、次に x1 行、次に x0x1 行と展開します (この例では、ここで停止しますが、実際の実装では 128 行まで展開します (最後の行は x6*…*x0))。

レビュー：

• ハイパーキューブのビットをグリッドに変換する

• 次に、各行の隣接するビットのグループをより大きな体の要素として扱い、それらに対して算術演算を実行して行をリードソロモン展開します。

• 次に、各列のビットの行の組み合わせを取り、各行のビットの列を出力として取得します（4 x 4より大きい正方形の場合ははるかに小さくなります）。

• 次に、出力を行列、そのビットを行として考える。

なぜこのようなことが起こるのでしょうか? 通常の数学では、数字を少しずつスライスしていくと、(通常の) 線形演算を任意の順序で実行して同じ結果を得るという能力が失われます。たとえば、345 という数字から始めて、8 倍、3 倍すると 8280 になり、この 2 つの演算を逆に行うと、やはり 8280 になります。しかし、2 つのステップの間にビットスライス演算を挿入すると、この能力が失われます。8 倍、3 倍すると、次のようになります。

しかし、3 倍、8 倍にすると、次のようになります。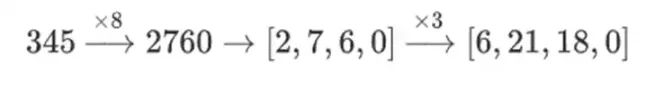

しかし、塔構造で構築されたバイナリフィールドでは、このアプローチは機能します。その理由は、それらの分離可能性です。大きな値に小さな値を掛けると、各セグメントで発生したことは各セグメントに留まります。1100101010001111に11を掛けると、これは1100101010001111の最初の分解と同じであり、

次に、各要素を 11 倍します。

すべてを一緒に入れて

一般的に、ゼロ知識証明システムは、多項式に関するステートメントを作成し、同時に基礎となる評価に関するステートメントを表すことによって機能します。フィボナッチの例で見たように、フィボナッチ計算のすべてのステップをチェックしながら、F(X+ 2)-F(X+ 1)-F(X) = Z(X)*H(X) です。ランダムなポイントで評価を証明することで、多項式に関するステートメントをチェックします。このランダムなポイントのチェックは、多項式全体のチェックを表します。多項式方程式が一致しない場合は、特定のランダムな座標で一致する可能性がわずかにあります。

実際には、非効率性の大きな原因の 1 つは、実際のプログラムでは、for ループのインデックス、True/False 値、カウンターなど、扱う数字のほとんどが小さいことです。ただし、リード ソロモン エンコーディングを使用してデータを拡張し、Merkle 証明ベースのチェックを安全にするために必要な冗長性を提供すると、元の値が小さくても、追加の値のほとんどがフィールドのサイズ全体を占めることになります。

これを修正するには、このフィールドをできるだけ小さくする必要があります。Plonky 2 では 256 ビットの数値から 64 ビットの数値に移行し、Plonky 3 ではさらに 31 ビットに削減しました。しかし、それでも最適ではありません。バイナリ フィールドでは、1 ビットで処理できます。これにより、エンコードが密になります。実際の基礎データが n ビットの場合、エンコードは n ビットになり、拡張は 8*n ビットになり、追加のオーバーヘッドはありません。

さて、このグラフをもう一度見てみましょう。

Binius では、多重線形多項式、つまりハイパーキューブ P(x0, x1,…xk) を扱います。ここで、単一の評価 P(0, 0, 0, 0)、P(0, 0, 0, 1) から P(1, 1, 1, 1) までが、必要なデータを保持します。特定の時点での計算を証明するために、同じデータを正方形として再解釈します。次に、リード・ソロモン符号化を使用して各行を拡張し、ランダム化された Merkle 分岐クエリに対するセキュリティに必要なデータ冗長性を提供します。次に、行のランダムな線形結合を計算し、新しい結合行に実際に必要な計算値が含まれるように係数を設計します。この新しく作成された行 (128 ビット行として再解釈) と、ランダムに選択された Merkle 分岐を持ついくつかの列が検証者に渡されます。

次に、検証者は拡張行の組み合わせ (正確には拡張列) と拡張行の組み合わせを実行し、2 つが一致することを確認します。次に、列の組み合わせを計算し、証明者が主張する値を返すかどうかを確認します。これが私たちの証明システム (正確には、証明システムの主要コンポーネントである多項式コミットメント スキーム) です。

まだカバーしていないものは何ですか?

• バリデーターの計算効率を実際に高めるには、行を拡張する効率的なアルゴリズムが必要です。ここで説明するバイナリ フィールドの高速フーリエ変換を使用します (ただし、この投稿では再帰拡張に基づかない効率の低い構造を使用しているため、正確な実装は異なります)。

• 算術的に。一変数多項式は、F(X+2)-F(X+1)-F(X) = Z(X)*H(X) のように計算の隣接するステップをリンクできるので便利です。ハイパーキューブでは、次のステップは X+1 よりも説明がはるかに不十分です。X+k、つまり k の累乗を実行できますが、このジャンプ動作により Binius の主要な利点の多くが犠牲になります。Binius の論文に解決策が説明されています (セクション 4.3 を参照)。ただし、これはそれ自体が深い迷路です。

• 特定の値チェックを安全に行う方法。フィボナッチの例では、重要な境界条件、つまり F(0)=F(1)=1 と F(100) の値をチェックする必要がありました。しかし、オリジナルの Binius では、既知の計算ポイントでチェックを行うのは安全ではありません。いわゆる合計チェック プロトコルを使用して、既知の計算チェックを未知の計算チェックに変換するかなり簡単な方法がいくつかありますが、ここでは取り上げません。

• 最近広く使用されているもう 1 つのテクノロジであるルックアップ プロトコルは、非常に効率的な証明システムを作成するために使用されます。Binius は、多くのアプリケーションでルックアップ プロトコルと組み合わせて使用できます。

• 平方根の検証時間を超える。平方根はコストがかかります。2^32 ビットの Binius 証明は約 11 MB の長さです。他の証明システムを使用して Binius 証明の証明を作成することでこれを補うことができ、より小さな証明サイズで Binius 証明の効率が得られます。もう 1 つのオプションは、より複雑な FRI-Binius プロトコルで、これは (通常の FRI と同様に) 多重対数サイズの証明を作成します。

• Binius が SNARK フレンドリー性に与える影響。簡単にまとめると、Binius を使用すると、計算を算術フレンドリーにする必要がなくなります。通常のハッシュは従来の算術ハッシュよりも効率的ではなくなり、2 の 32 乗を法とする乗算や 2 の 256 乗を法とする乗算は、2 を法とする乗算ほど面倒ではなくなります。ただし、これは複雑なトピックです。すべてがバイナリで行われると、多くのことが変わります。

今後数か月で、バイナリ フィールド ベースの証明テクノロジがさらに改善されることを期待しています。

この記事はインターネットから引用したものです: Vitalik: Binius、バイナリフィールドの効率的な証明

関連：BNBコインが回復の兆し：新たな年間最高値が見えてきた

要約 BNB 価格は $550 から反発し、$593 抵抗を突破する寸前まで来ています。価格指標は強気の勢いを取り戻し、8% の上昇を支えています。シャープレシオは 4.03 で、新しい投資家を取引所トークンに向かわせる可能性が高いでしょう。3 月は BNB コインにとって好ましい月でした。この暗号通貨は、わずか数日間で今年の最高値を 2 回達成した後、調整を経験しました。ほぼ 2 週間の回復期間を経て、BNB コインは 2024 年に新たな最高値に到達する可能性がある兆候を示しています。しかし、そのようなマイルストーンは達成可能でしょうか? BNB は有望に見えます $550 サポートレベルからの反発を受けて、この分析の時点で BNB コインの価値は $581 に上昇しました。この改善は、アルトコインのリスク リターン プロファイルの回復を反映しています。