ゼロ知識証明の高度な形式検証: ゼロ知識メモリを証明する方法

ブログシリーズでは ゼロ知識証明の高度な形式検証 、私たちは議論しました ZK命令の検証方法 そして 2つのZK脆弱性を詳しく調査 すべてのzkWasm命令を正式に検証することで、すべての脆弱性を発見して修正し、図に示すように、zkWasm回路全体の技術的な安全性と正確性を完全に検証することができました。 公開レポート そして コードリポジトリ .

zkWasm 命令の検証プロセスを示し、プロジェクトの初期コンセプトを紹介しましたが、形式検証に精通している読者は、検証において他の小規模な ZK システムや他のタイプのバイトコード VM と比較した zkVM の独自性を理解することに興味があるかもしれません。この記事では、zkWasm メモリ サブシステムを検証する際に遭遇するいくつかの技術的なポイントについて詳しく説明します。メモリは zkVM の最もユニークな部分であり、メモリを適切に処理することが他のすべての zkVM を検証する上で重要です。

形式検証: 仮想マシン (VM) と ZK 仮想マシン (zkVM)

私たちの最終的な目標は、通常のバイトコードインタープリタ（Ethereumノードで使用されるEVMインタープリタなどのVM）の正当性定理と同様に、zkWasmの正当性を検証することです。つまり、インタープリタの各実行ステップは、言語の操作的意味論に基づく正当なステップに対応しています。下の図に示すように、バイトコードインタープリタのデータ構造の現在の状態がSLであり、この状態がWasmマシンの高レベル仕様で状態SHとしてマークされている場合、インタープリタが状態SLに進むと、対応する正当な高レベル状態SHが存在する必要があり、Wasm仕様ではSHがSHに進む必要があると規定されています。

同様に、zkVM にも同様の正当性定理があります。zkWasm 実行テーブルの各新しい行は、言語の操作的意味論に基づく正当なステップに対応します。下の図に示すように、実行テーブル データ構造の行の現在の状態が SR であり、この状態が Wasm マシンの高レベル仕様で状態 SH として表される場合、実行テーブル状態 SR の次の行は高レベル状態 SH に対応する必要があり、Wasm 仕様では SH が SH にステップする必要があることが規定されています。

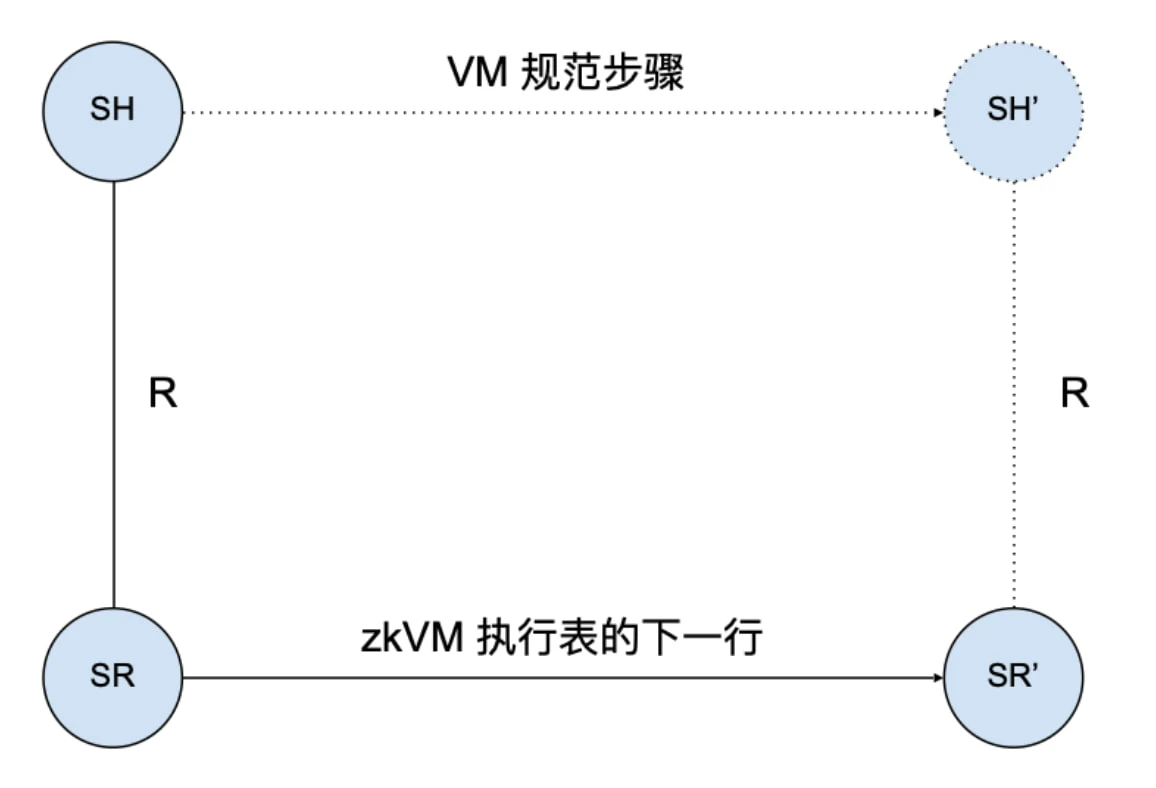VM と zkVM の両方で高レベル状態と Wasm ステップの仕様が一貫していることがわかります。そのため、プログラミング言語インタープリタやコンパイラの以前の検証経験を参考にすることができます。zkVM 検証の特徴は、システムの低レベル状態を構成するデータ構造の種類にあります。

まず、 以前のブログ投稿 zk 証明器は本質的に大きな素数を法とする整数演算であり、Wasm 仕様と通常のインタープリタは 32 ビットまたは 64 ビットの整数を扱います。zkVM 実装の多くはこれを扱うため、検証でもこれを処理する必要があります。ただし、これはローカルな問題です。算術演算を処理する必要があるため、コードの各行はより複雑になりますが、コードと証明の全体的な構造は変わりません。

もう 1 つの大きな違いは、動的にサイズ調整されるデータ構造の扱い方です。通常のバイトコード インタプリタでは、メモリ、データ スタック、コール スタックはすべて可変データ構造として実装されます。同様に、Wasm 仕様ではメモリを get/set メソッドを持つデータ型として表現します。たとえば、Geths EVM インタプリタには、物理メモリを表すバイト配列として実装され、`Set 32` メソッドと `GetPtr` メソッドを通じて読み書きされる `Memory` データ型があります。 メモリストア命令 、Geth は物理メモリを変更するために `Set 32` を呼び出します。

func opMstore(pc *uint 64, インタープリタ *EVMInterpreter, スコープ *ScopeContext) ([]byte, error) {

// スタックの値をポップする

mStart、val := scope.Stack.pop()、scope.Stack.pop()

スコープ.メモリ.セット32(mStart.Uint64(), val)

nil、nilを返す

}

上記のインタープリタの正しさの証明では、インタープリタ内の具体的なメモリと仕様内の抽象メモリに値を割り当てた後、高レベルの状態が低レベルの状態と一致することを証明するのは比較的簡単です。

ただし、zkVM では状況がさらに複雑になります。

zkWasms メモリテーブルとメモリ抽象化レイヤー

zkVM では、実行テーブルには固定サイズのデータ用の列 (CPU のレジスタに類似) がありますが、補助テーブルを介してアクセスされる動的サイズのデータ構造は処理できません。zkWasm 実行テーブルには、1、2、3 などの値を持つ EID 列と、メモリ データとコール スタックを表すメモリ テーブルとジャンプ テーブルの 2 つの補助テーブルがあります。

以下は引き出しプログラムの実装例です。

int 残高、金額;

void main() {

残高 = 100;

金額 = 10;

残高 -= 金額; // 引き出し

}

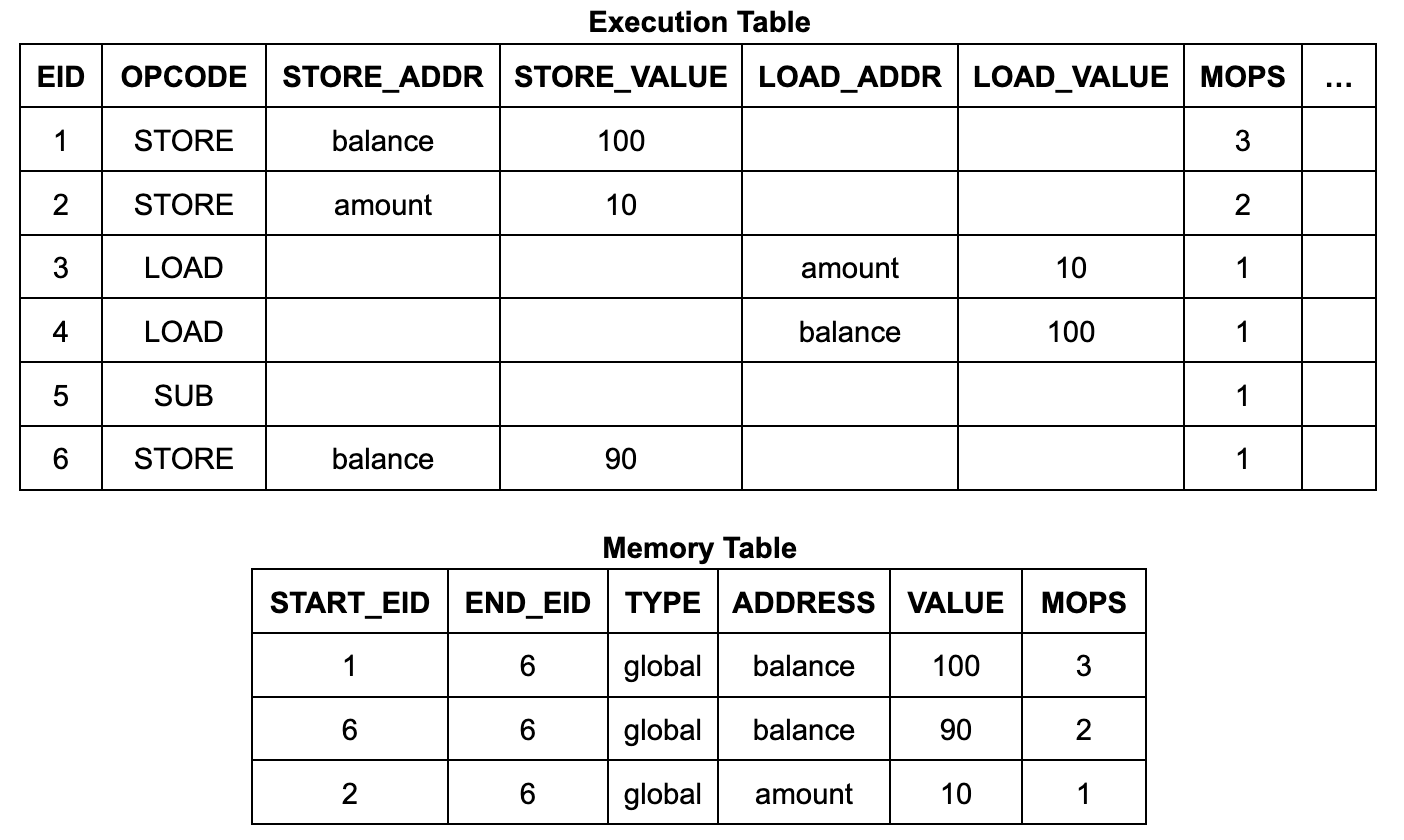
実行テーブルの内容と構造は非常にシンプルです。実行テーブルには 6 つの実行ステップ (EID 1 ～ 6) があり、各ステップには操作コード (オペコード) と、命令がメモリの読み取りまたは書き込みの場合はアドレスとデータがリストされた行があります。

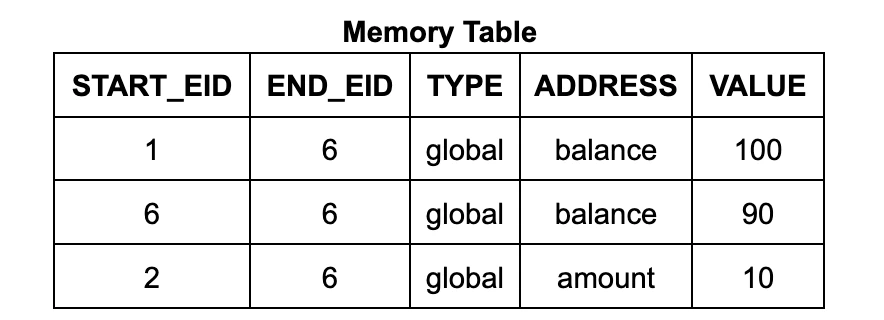
メモリ テーブルの各行には、アドレス、データ、開始 EID、終了 EID が含まれます。開始 EID は、そのアドレスにデータを書き込んだ実行ステップの EID であり、終了 EID は、そのアドレスに書き込む次の実行ステップの EID です。(カウントも含まれますが、これについては後で詳しく説明します。) Wasm メモリ読み取り命令回路では、ルックアップ制約を使用して、読み取り命令の EID が開始から終了までの範囲内になるように、テーブル内に適切なテーブル エントリがあることを確認します。(同様に、ジャンプ テーブルの各行は呼び出しスタックのフレームに対応し、各行には、それを作成した呼び出し命令ステップの EID がラベル付けされます。)

このメモリ システムは、通常の VM インタープリターとは大きく異なります。メモリ テーブルは、徐々に更新される可変メモリではなく、実行トレース全体のすべてのメモリ アクセスの履歴が含まれています。プログラマーの作業を簡素化するために、zkWasm は、2 つの便利なエントリ関数を通じて実装される抽象化レイヤーを提供します。これらは次のとおりです。

alloc_memory_table_lookup_write_cell

そして

割り当てメモリテーブルルックアップ読み取りセル

パラメータは次のとおりです。

たとえば、zkWasm のメモリ ストア命令を実装するコードには、write alloc 関数の呼び出しが含まれています。

memory_table_lookup_heap_write1 = アロケータとする

.alloc_memory_table_lookup_write_cell_with_value(

書き込み res 1 を保存、

制約ビルダー、

イード、

|____| constant_from!(LocationType::Heap を u 64 として移動)、

移動 |meta| load_block_index.expr(meta), // アドレス

move |____| constant_from!(0), // 32ビット

move |____| constant_from!( 1), // (常に)有効

);

store_value_in_heap1 を memory_table_lookup_heap_write1.value_cell とします。

`alloc` 関数は、テーブル間の検索制約と、現在の `eid` をメモリ テーブル エントリに関連付ける算術制約を処理する役割を担います。したがって、プログラマーはこれらのテーブルを通常のメモリとして扱うことができ、コードの実行後には `store_value_in_heap1` の値が `load_block_index` アドレスに割り当てられます。

同様に、メモリ読み取り命令は `read_alloc` 関数を使用して実装されます。上記の実行シーケンスの例では、各ロード命令には読み取り制約があり、各ストア命令には書き込み制約があり、各制約はメモリ テーブル内のエントリによって満たされます。

mtable_lookup_write(行 1.eid、行 1.store_addr、行 1.store_value)

⇐ (行 1.eid= 1 ∧ 行 1.store_addr=balance ∧ 行 1.store_value= 100 ∧ …)

mtable_lookup_write(行 2.eid、行 2.store_addr、行 2.store_value)

⇐ (行 2.eid= 2 ∧ 行 2.store_addr= 金額 ∧ 行 2.store_value= 10 ∧ …)

mtable_lookup_read(行 3.eid、行 3.load_addr、行 3.load_value)

⇐ （ 2

mtable_lookup_read(行 4.eid、行 4.load_addr、行 4.load_value)

⇐ （ 1

mtable_lookup_write(行 6.eid、行 6.store_addr、行 6.store_value)

⇐ (行 6.eid= 6 ∧ 行 6.store_addr=balance ∧ 行 6.store_value= 90 ∧ …)

形式検証の構造は、検証対象のソフトウェアで使用される抽象化に対応している必要があります。これにより、証明はコードと同じロジックに従うことができます。zkWasm の場合、これは、メモリ テーブル回路と alloc 読み取り/書き込みセル機能を、可変メモリのようなインターフェイスを使用してモジュールとして検証する必要があることを意味します。このようなインターフェイスがあれば、各命令回路の検証は通常のインタープリターと同様の方法で実行でき、追加の ZK 複雑性はメモリ サブシステム モジュールにカプセル化されます。

検証では、メモリ テーブルを実際には変更可能なデータ構造と見なすことができるというアイデアを具体的に実装しました。つまり、メモリ テーブルを完全にスキャンし、対応するアドレス データ マッピングを構築する関数 `memory_at type` を作成しました。(ここで、変数 `type` の値の範囲は、ヒープ、データ スタック、およびグローバル変数という 3 つの異なるタイプの Wasm メモリ データです。) 次に、alloc 関数によって生成されたメモリ制約が、set 関数と get 関数を使用して対応するアドレス データ マッピングに加えられたデータ変更と同等であることを証明しました。次のことを証明できます。

• 各eidについて、以下の制約が成り立つ場合

memory_table_lookup_read_cell eid タイプ オフセット値

しかし

get (memory_at eid type) offset = ある値

• そして、以下の制約が成り立つ場合

memory_table_lookup_write_cell eid タイプ オフセット値

しかし

memory_at (eid+ 1) type = set (memory_at eid type) オフセット値

その後、各命令の検証は、非 ZK バイトコード インタープリターと同様に、アドレス データ マッピングの get および set 操作に基づいて行うことができます。

zkWasms メモリ書き込みカウントメカニズム

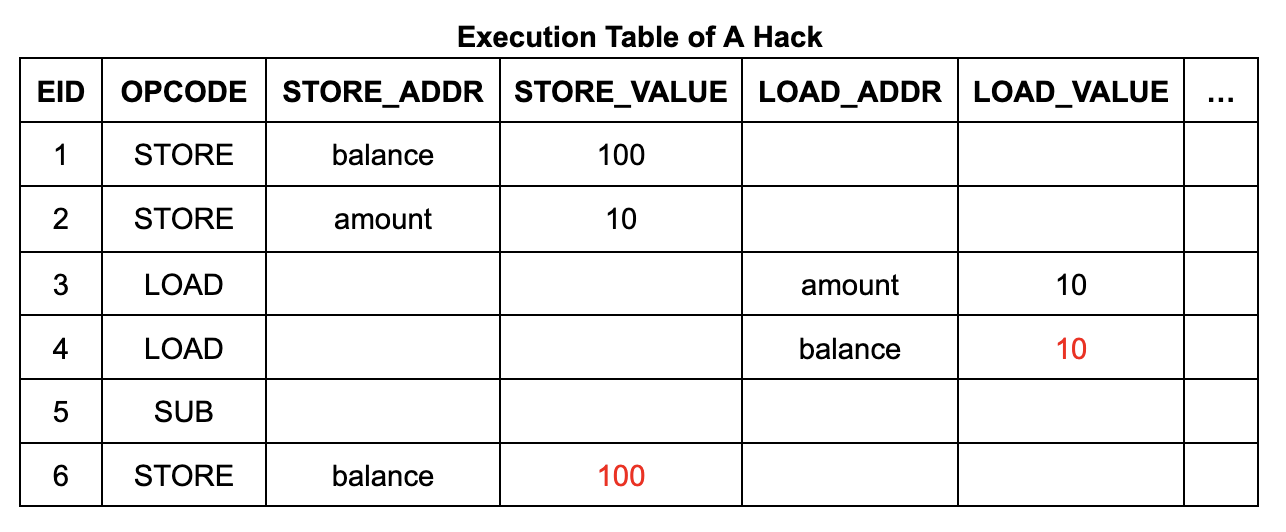
ただし、上記の簡略化された説明では、メモリ テーブルとジャンプ テーブルの完全な内容は明らかにされていません。zkVM のフレームワークでは、攻撃者がこれらのテーブルを操作する可能性があり、攻撃者はメモリ ロード命令を簡単に操作して、データ行を挿入することで任意の値を返すことができます。

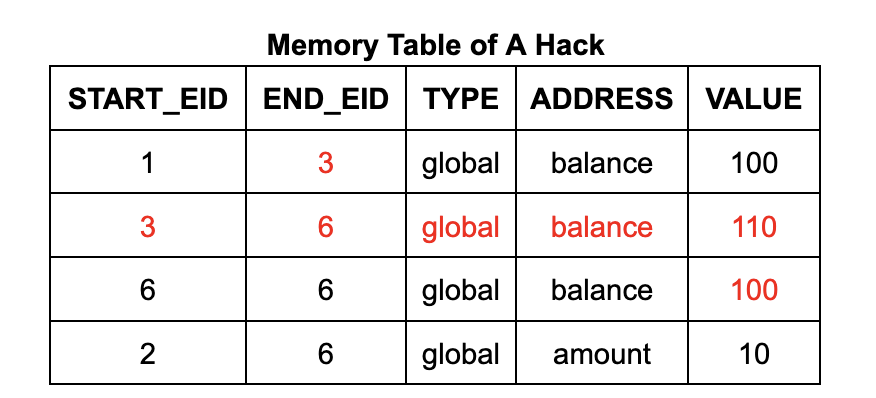
引き出しプログラムを例にとると、攻撃者は引き出し操作の前に $110 のメモリ書き込み操作を偽造することで、口座残高に偽のデータを挿入する機会があります。このプロセスは、メモリ テーブルにデータ行を追加し、メモリ テーブルと実行テーブル内の既存のセルの値を変更することで実現できます。これにより、操作後も口座残高が $100 のままであるため、引き出し操作が自由に実行できるようになります。

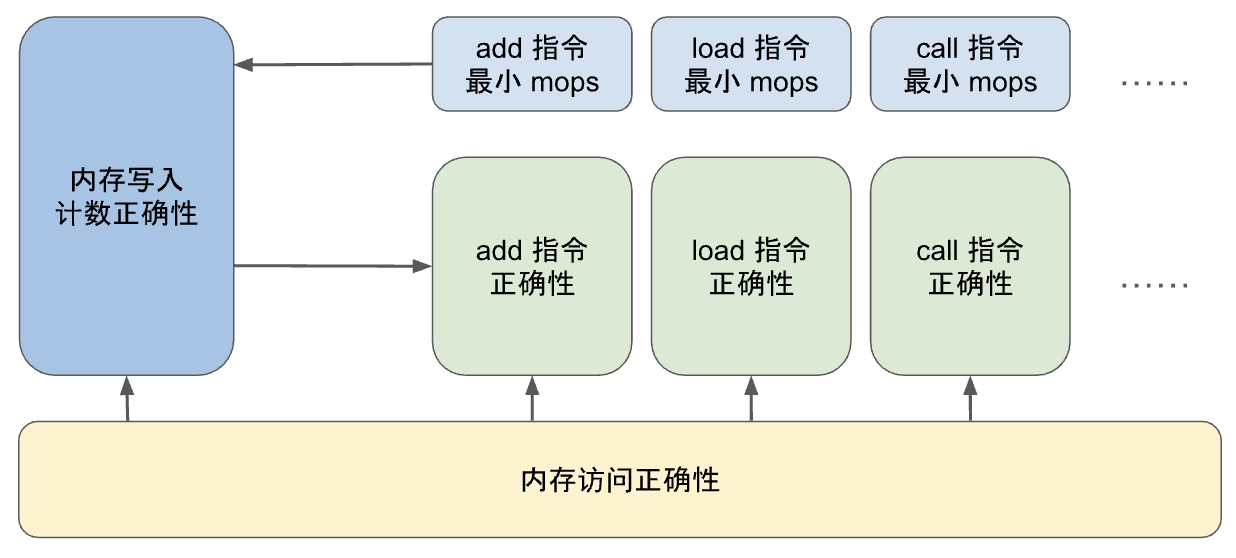
メモリ テーブル (およびジャンプ テーブル) に、実際に実行されたメモリ書き込み (および呼び出しと戻り) によって生成された有効なエントリのみが含まれるようにするために、zkWasm は特別なカウント メカニズムを使用してエントリの数を監視します。具体的には、メモリ テーブルには、メモリ書き込みエントリの合計数を追跡する専用の列があります。同時に、実行テーブルには、各命令で予想されるメモリ書き込み操作の数をカウントするカウンターも含まれています。2 つのカウントが一貫していることを確認するために、等式制約が設定されています。このアプローチのロジックは非常に直感的です。メモリ書き込み操作が実行されるたびに、1 回カウントされ、メモリ テーブルに対応するレコードが存在するはずです。したがって、攻撃者はメモリ テーブルに追加のエントリを挿入できません。

上記の論理的記述は少し曖昧なので、機械的証明の過程で、より正確にする必要があります。まず、上記のメモリ書き込み補題の記述を修正する必要があります。指定された `eid` と `type` を持つメモリ テーブル エントリの数をカウントする関数 `mops_at eid type` を定義します (ほとんどの命令は、eid で 0 または 1 のエントリを作成します)。定理の完全な記述には、誤ったメモリ テーブル エントリが存在しないという追加の前提条件があります。

以下の制約が成り立つ場合

(memory_table_lookup_write_cell eid タイプ オフセット値)

そして、次の新しい制約が成立する。

(mops_at eid タイプ) = 1

しかし

(memory_at(eid+ 1) type) = (memory_at eid type) オフセット値を設定します

これには、前のケースよりも正確な検証が必要です。等式制約から、メモリ テーブル エントリの合計数が実行時のメモリ書き込みの合計数に等しいと単純に結論付けるだけでは不十分です。命令の正しさを証明するには、各命令が正しい数のメモリ テーブル エントリに対応していることを知る必要があります。たとえば、攻撃者が実行シーケンス内の命令のメモリ テーブル エントリを省略し、別の無関係な命令に対して悪意のある新しいメモリ テーブル エントリを作成する可能性を排除する必要があります。

これを証明するには、特定の命令の memtable エントリの数を制限するトップダウン アプローチを採用します。このアプローチは 3 つのステップで構成されます。まず、命令の種類に基づいて、実行シーケンス内の命令に対して作成する必要があるエントリの数を見積もります。i 番目のステップから実行終了までの予想される書き込み数を `instructions_mops i` と呼び、i 番目の命令から実行終了までの対応する memtable エントリ数を `cum_mops (eid i)` と呼びます。各命令のルックアップ制約を分析することで、予想されるエントリ数よりも少ないエントリが作成されないこと、つまり追跡される各セグメント [i… numRows] によって作成されるエントリ数が予想数よりも少ないことを証明できます。

補題 cum_mops_bound: forall ni,

0 ≤ i ->

i + Z.of_nat n = etable_numRow ->

MTable.cum_mops (etable_values eid_cell i) (max_eid+ 1) ≥ instructions_mops i n。

第二に、テーブルに予想以上のエントリがないことを示すことができれば、エントリの数は正確に正しいことになり、これは明らかです。

補題 cum_mops_equal : forall ni,

0 ≤ i ->

i + Z.of_nat n = etable_numRow ->

MTable.cum_mops (etable_values eid_cell i) (max_eid+ 1) ≤ instructions_mops in ->

MTable.cum_mops (etable_values eid_cell i) (max_eid+ 1) = instructions_mops i n.

次にステップ 3 に進みます。正当性定理によれば、任意の n に対して、cum_mops と instructions_mops は、テーブルの行 n から最後までの部分で常に一致します。

補題 cum_mops_equal : forall n,

0

MTable.cum_mops (etable_values eid_cell (Z.of_nat n)) (max_eid+ 1) = instructions_mops (Z.of_nat n)

検証は n の帰納法によって行われます。表の最初の行は zkWasm の等式制約であり、メモリ テーブル内のエントリの合計数が正しいこと、つまり cum_mops 0 = instructions_mops 0 であることを示しています。次の行については、帰納法の仮説によって次のことがわかります。

cum_mops n = 指示_mops n

そして私たちは証明したいと考えています

cum_mops (n+ 1) = instructions_mops (n+ 1)

ここに注意してください

cum_mops n = mop_at n + cum_mops (n+ 1)

そして

命令_mops n = 命令_mops n + 命令_mops (n+ 1)

したがって、

mops_at n + cum_mops (n+ 1) = instruction_mops n + instructions_mops (n+ 1)

先ほど、各命令は期待される数以上のエントリを作成することを示しました。

mops_at n ≥ instruction_mops n。

つまり、

cum_mops (n+ 1) ≤ instructions_mops (n+ 1)

ここで、上で述べた 2 番目の補題を適用する必要があります。

（同様の補題をジャンプテーブルに適用して、すべての呼び出し命令が正確に1つのジャンプテーブルエントリを生成することを証明することができ、証明手法は一般的に適用可能です。しかし、戻り命令の正しさを証明するにはさらなる作業が必要です。戻りeidは、呼び出しフレームを作成した呼び出し命令のeidとは異なるため、 追加の不変量 これは、eid 値が実行シーケンス内で一方向に増加していることを示しています。

証明のこのような詳細な記述は形式検証の典型であり、特定のコードの検証がコードを書くよりも時間がかかることが多い理由です。しかし、それだけの価値があるのでしょうか? この場合は価値があります。なぜなら、証明中にジャンプテーブルカウントメカニズムに重大なバグが見つかったからです。このバグの詳細は、 以前の投稿 要約すると、古いバージョンのコードでは呼び出し命令と戻り命令の両方がカウントされていたため、攻撃者は実行シーケンスに余分な戻り命令を追加することで、偽のジャンプ テーブル エントリのためのスペースを作ることができました。誤ったカウント メカニズムは、すべての呼び出し命令と戻り命令をカウントするという直感を満たしていますが、この直感をより正確な定理ステートメントに洗練しようとすると、問題が明らかになります。

証明プロセスをモジュール化する

上記の議論から、各命令回路に関する証明と実行テーブルのカウント列に関する証明の間には循環依存関係があることがわかります。命令回路の正しさを証明するには、その中のメモリ書き込みについて推論する必要があります。つまり、特定の EID のメモリ テーブル エントリの数を知る必要があり、実行テーブル内のメモリ書き込み操作のカウントが正しいことを証明する必要があります。そのためには、各命令が少なくとも最小数のメモリ書き込み操作を実行することを証明する必要があります。

さらに、考慮すべきもう 1 つの要素があります。zkWasm プロジェクトは非常に大きいため、検証作業をモジュール化して、複数の検証エンジニアが作業を分担できるようにする必要があります。したがって、カウント メカニズムの証明を分解するときは、その複雑さに特別な注意を払う必要があります。たとえば、LocalGet 命令の場合、次の 2 つの定理があります。

定理 opcode_mops_correct_local_get : forall i,

0

etable_values eid_cell i > 0 ->

opcode_mops_correct ローカル取得 i。

定理 LocalGetOp_correct : すべての i st y xs について、

0

etable_values 有効なセル i = 1 ->

mops_at_correct i ->

etable_values (ops_cell LocalGet) i = 1 ->

state_rel i st ->

wasm_stack st = xs ->

(etable_values offset_cell i) > 1 ->

nth_error xs (Z.to_nat (etable_values offset_cell i – 1)) = あるy ->

state_rel (i+ 1) (update_stack (incr_iid st) (y::xs))。

第一定理の記述

opcode_mops_correct ローカル取得 i

定義が展開されると、命令が行 i に少なくとも 1 つの memtable エントリを作成することを意味します (数値 1 は zkWasm の LocalGet オペコード仕様で指定されています)。

2番目の定理は、この命令の完全な正当性定理であり、

mops_at_correct 私

仮説としては、これは命令が正確に 1 つのメモリ テーブル エントリを作成することを意味します。

検証エンジニアは、これら 2 つの定理を個別に証明し、実行テーブルに関する証明と組み合わせて、システム全体の正しさを証明できます。メモリ テーブルの具体的な実装を知らなくても、個々の命令のすべての証明を読み取り/書き込み制約のレベルで実行できることは注目に値します。したがって、プロジェクトは独立して処理できる 3 つの部分に分割されています。

要約する

zkVM 回路を 1 行ずつ検証することは、他の ZK アプリケーションの検証と基本的に違いはありません。これらはすべて、算術制約について同様の推論を必要とするためです。高レベルでは、zkVM の検証には、プログラミング言語インタープリターとコンパイラーの形式検証で使用されるのと同じ手法の多くが必要です。ここでの主な違いは、仮想マシンの状態が動的にサイズ調整されることです。ただし、実装で使用される抽象化レベルに合わせて検証構造を慎重に構築することで、これらの違いの影響を最小限に抑えることができます。これにより、通常のインタープリターと同様に、get-set インターフェイスに基づいて各命令をモジュールごとに個別に検証できます。

この記事はインターネットから引用したものです: ゼロ知識証明の高度な形式検証: ゼロ知識メモリを証明する方法