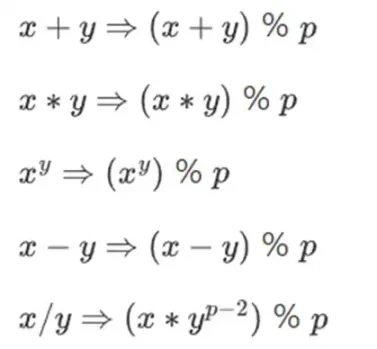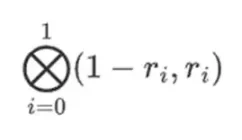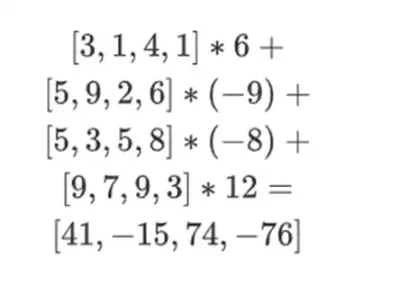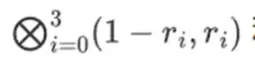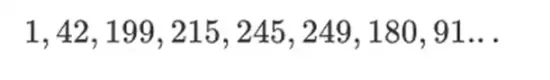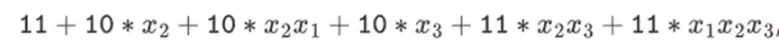Vitalik: Binius, bukti efisien untuk bidang biner

Artikel asli oleh: Vitalik Buterin

Terjemahan asli: Kate, MarsBit

Posting ini terutama ditujukan untuk pembaca yang umumnya akrab dengan kriptografi era 2019, khususnya SNARK dan STARK. Jika belum, saya sarankan untuk membacanya terlebih dahulu. Terima kasih khusus kepada Justin Drake, Jim Posen, Benjamin Diamond, dan Radi Cojbasic atas masukan dan komentar mereka.

Selama dua tahun terakhir, STARK telah menjadi teknologi utama dan tak tergantikan untuk membuat bukti kriptografi yang mudah diverifikasi secara efisien atas pernyataan yang sangat kompleks (misalnya membuktikan bahwa blok Ethereum valid). Salah satu alasan utama untuk ini adalah ukuran bidang yang kecil: SNARK berdasarkan kurva eliptik mengharuskan Anda bekerja pada bilangan bulat 256-bit agar cukup aman, sementara STARK memungkinkan Anda menggunakan ukuran bidang yang jauh lebih kecil dengan efisiensi yang lebih tinggi: pertama bidang Goldilocks (bilangan bulat 64-bit), kemudian Mersenne 31 dan BabyBear (keduanya 31 bit). Karena perolehan efisiensi ini, Plonky 2 yang menggunakan Goldilocks ratusan kali lebih cepat daripada pendahulunya dalam membuktikan berbagai jenis perhitungan.

Pertanyaan wajarnya adalah: bisakah kita membawa tren ini ke kesimpulan logisnya dan membangun sistem pembuktian yang berjalan lebih cepat dengan beroperasi langsung pada angka nol dan satu? Inilah yang coba dilakukan Binius, menggunakan sejumlah trik matematika yang membuatnya sangat berbeda dari SNARK dan STARK tiga tahun lalu. Posting ini menjelaskan mengapa bidang kecil membuat pembuatan bukti lebih efisien, mengapa bidang biner sangat kuat, dan trik yang digunakan Binius untuk membuat pembuktian pada bidang biner menjadi sangat efisien.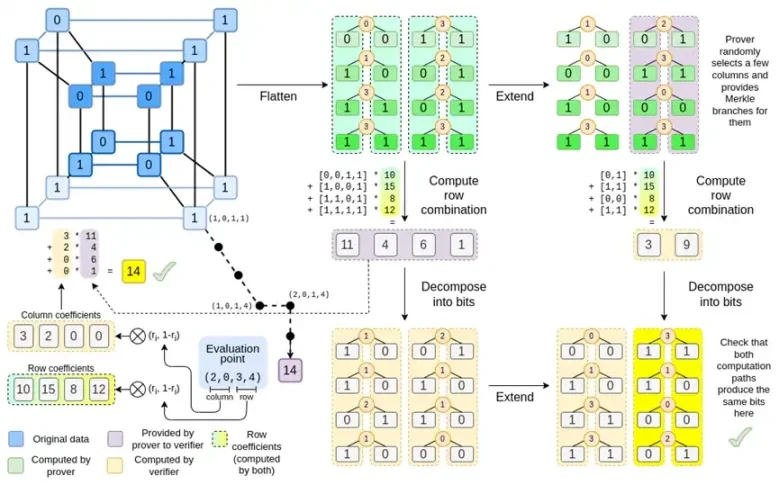

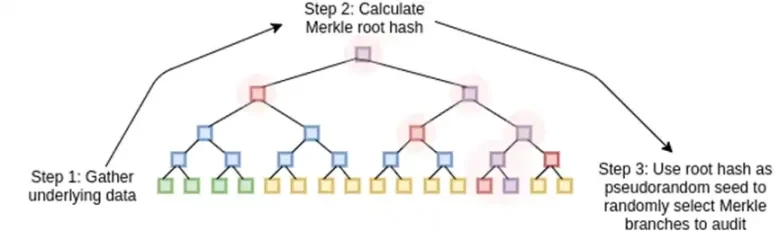
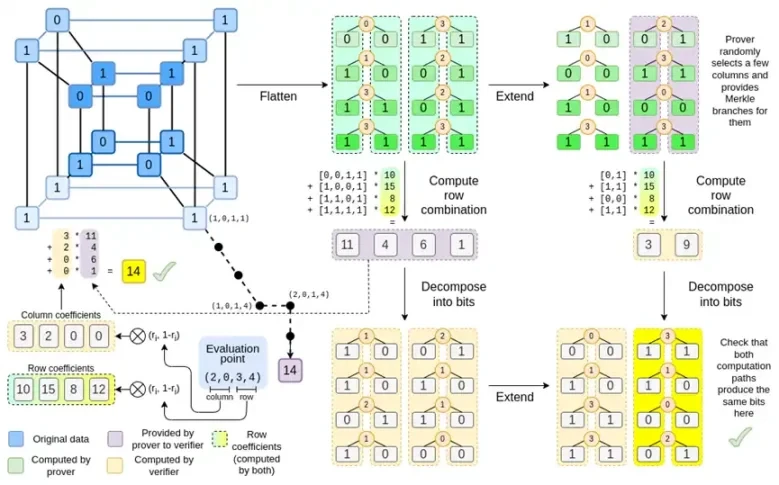
Binius, di akhir postingan ini, Anda seharusnya sudah bisa memahami setiap bagian diagram ini.

Ulasan: bidang terbatas

Salah satu tugas utama sistem pembuktian kriptografi adalah mengoperasikan data dalam jumlah besar sambil menjaga jumlahnya tetap kecil. Jika Anda dapat memampatkan pernyataan tentang suatu program besar menjadi persamaan matematika yang berisi beberapa angka, tetapi angka tersebut sama besarnya dengan program aslinya, maka Anda tidak memperoleh apa pun.

Untuk melakukan aritmatika kompleks sambil menjaga angka tetap kecil, kriptografer sering kali menggunakan aritmatika modular. Kami memilih modulus bilangan prima p. Operator % artinya mengambil sisanya: 15% 7 = 1, 53% 10 = 3, dan seterusnya. (Perhatikan bahwa jawabannya selalu non-negatif, jadi misalnya -1% 10 = 9)

Anda mungkin pernah melihat aritmatika modular dalam konteks penjumlahan dan pengurangan waktu (misalnya, jam berapa sekarang 4 jam setelah jam 9?). Namun di sini, kita tidak hanya menambah dan mengurangi modulo suatu bilangan; kita juga bisa mengalikan, membagi, dan mengambil eksponen.

Kami mendefinisikan ulang:

Aturan di atas semuanya konsisten. Misalnya, jika p = 7, maka:

5 + 3 = 1 (karena 8% 7 = 1)

1-3 = 5 (karena -2% 7 = 5)

2* 5 = 3

3/5 = 2

Istilah yang lebih umum untuk struktur tersebut adalah bidang berhingga. Bidang berhingga adalah struktur matematika yang mengikuti hukum aritmatika biasa, namun jumlah nilai yang mungkin terbatas, sehingga setiap nilai dapat diwakili oleh ukuran tetap.

Aritmatika modular (atau bidang prima) adalah jenis bidang berhingga yang paling umum, namun ada jenis lain: bidang ekstensi. Anda mungkin pernah melihat satu bidang tambahan: bilangan kompleks. Kita membayangkan sebuah elemen baru dan memberinya label i, lalu menghitungnya: (3i+2)*(2i+4)=6i*i+12i+4i+8=16i+2. Kita dapat melakukan hal yang sama dengan perluasan bidang prima. Saat kita mulai menangani bidang yang lebih kecil, ekstensi bidang utama menjadi semakin penting untuk keamanan, dan bidang biner (digunakan oleh Binius) sepenuhnya bergantung pada ekstensi untuk mendapatkan kegunaan praktis.

Ulasan: Aritmatika

Cara SNARK dan STARK membuktikan program komputer adalah melalui aritmatika: Anda mengambil pernyataan tentang program yang ingin Anda buktikan, dan mengubahnya menjadi persamaan matematika yang melibatkan polinomial. Solusi yang valid terhadap persamaan tersebut berhubungan dengan eksekusi program yang valid.

Sebagai contoh sederhana, misalkan saya menghitung angka Fibonacci ke-100 dan saya ingin membuktikan kepada Anda berapa angka tersebut. Saya membuat polinomial F yang mengkodekan deret Fibonacci: jadi F(0)=F(1)=1, F(2)=2, F(3)=3, F(4)=5 dan seterusnya untuk 100 langkah . Kondisi yang perlu saya buktikan adalah F(x+2)=F(x)+F(x+1) pada seluruh rentang x={0, 1…98}. Saya dapat meyakinkan Anda dengan memberi Anda hasil bagi:

dimana Z(x) = (x-0) * (x-1) * …(x-98). . Jika saya dapat menyatakan bahwa F dan H memenuhi persamaan ini, maka F harus memenuhi F(x+ 2)-F(x+ 1)-F(x) dalam rentang tersebut. Jika saya juga memverifikasi bahwa untuk F, F(0)=F(1)=1, maka F(100) pastilah bilangan Fibonacci ke-100.

Jika Anda ingin membuktikan sesuatu yang lebih rumit, gantilah relasi sederhana F(x+2) = F(x) + F(x+1) dengan persamaan yang lebih rumit yang pada dasarnya menyatakan F(x+1) adalah outputnya menginisialisasi mesin virtual dengan status F(x), dan menjalankan satu langkah komputasi. Anda juga bisa mengganti angka 100 dengan angka yang lebih besar, misalnya 100000000, untuk menampung langkah yang lebih banyak.

Semua SNARK dan STARK didasarkan pada gagasan penggunaan persamaan sederhana atas polinomial (dan terkadang vektor dan matriks) untuk mewakili sejumlah besar hubungan antara nilai-nilai individual. Tidak semua algoritme memeriksa kesetaraan antara langkah-langkah komputasi yang berdekatan seperti di atas: misalnya, PLONK tidak memeriksanya, begitu pula R1CS. Namun banyak pemeriksaan yang paling efektif melakukan hal ini, karena lebih mudah untuk meminimalkan overhead dengan melakukan pemeriksaan yang sama (atau beberapa pemeriksaan yang sama) berkali-kali.

Plonky 2: Dari SNARK dan STARK 256-bit hingga 64-bit… hanya STARK

Lima tahun yang lalu, ringkasan yang masuk akal tentang berbagai jenis bukti tanpa pengetahuan adalah sebagai berikut. Ada dua jenis pembuktian: SNARK (berbasis kurva elips) dan STARK (berbasis hash). Secara teknis, STARK adalah sejenis SNARK, namun dalam praktiknya, “SNARK” biasanya digunakan untuk merujuk pada varian berbasis kurva elips dan “STARK” untuk merujuk pada konstruksi berbasis hash. SNARK berukuran kecil, sehingga Anda dapat memverifikasinya dengan sangat cepat dan menginstalnya secara on-chain dengan mudah. STARK berukuran besar, tetapi tidak memerlukan pengaturan yang tepercaya, dan tahan terhadap kuantum.

STARK bekerja dengan memperlakukan data sebagai polinomial, menghitung komputasi polinomial tersebut, dan menggunakan akar Merkle dari data yang diperluas sebagai “komitmen polinomial”.

Bagian penting dari sejarah di sini adalah bahwa SNARK berbasis kurva elips pertama kali digunakan secara luas: STARK belum menjadi cukup efisien hingga sekitar tahun 2018, berkat FRI, dan pada saat itu Zcash telah berjalan selama lebih dari setahun. SNARK berbasis kurva elips memiliki batasan utama: jika Anda ingin menggunakan SNARK berbasis kurva elips, maka aritmatika dalam persamaan ini harus dilakukan modulo jumlah titik pada kurva elips. Ini adalah angka yang besar, biasanya mendekati 2 pangkat 256: misalnya, untuk kurva bn128 adalah 21888242871839275222246405745257275088548364400416034343698204186575808495617. Namun komputasi sebenarnya menggunakan angka yang kecil: jika Anda berpikir tentang program nyata dalam bahasa favorit Anda, sebagian besarnya kegunaannya adalah penghitung, indeks dalam perulangan for, posisi dalam program, bit tunggal yang mewakili Benar atau Salah, dan hal-hal lain yang hampir selalu hanya terdiri dari beberapa digit.

Meskipun data asli Anda terdiri dari angka-angka kecil, proses pembuktiannya memerlukan penghitungan hasil bagi, perluasan, kombinasi linier acak, dan transformasi data lainnya yang akan menghasilkan jumlah objek yang sama atau lebih besar yang rata-rata sama besarnya dengan ukuran penuh objek Anda. bidang. Hal ini menciptakan inefisiensi utama: untuk membuktikan penghitungan pada n nilai kecil, Anda harus melakukan lebih banyak penghitungan pada n nilai yang jauh lebih besar. Awalnya, STARK mewarisi kebiasaan SNARK menggunakan bidang 256-bit, dan karenanya mengalami inefisiensi yang sama.

Perluasan Reed-Solomon dari beberapa evaluasi polinomial. Meskipun nilai aslinya kecil, nilai tambahan diperluas hingga ukuran penuh bidang (dalam hal ini 2^31 – 1)

Pada tahun 2022, Plonky 2 dirilis. Inovasi utama Plonky 2 adalah melakukan aritmatika modulo bilangan prima yang lebih kecil: 2 pangkat 64 – 2 pangkat 32 + 1 = 18446744067414584321. Kini, setiap penjumlahan atau perkalian selalu dapat dilakukan dalam beberapa instruksi pada CPU, dan hashing semua data bersama-sama 4 kali lebih cepat dari sebelumnya. Namun ada masalah: metode ini hanya berfungsi untuk STARK. Jika Anda mencoba menggunakan SNARK, kurva elips menjadi tidak aman untuk kurva elips yang kecil.

Untuk menjamin keamanan, Plonky 2 juga perlu memperkenalkan bidang ekstensi. Teknik utama untuk memeriksa persamaan aritmatika adalah pengambilan sampel titik acak: jika Anda ingin memeriksa apakah H(x) * Z(x) sama dengan F(x+ 2)-F(x+ 1)-F(x), Anda dapat secara acak pilih koordinat r, berikan komitmen polinomial untuk membuktikan H(r), Z(r), F(r), F(r+ 1) dan F(r+ 2), lalu verifikasi apakah H(r) * Z(r ) sama dengan F(r+ 2)-F(r+ 1)- F(r). Jika penyerang dapat menebak koordinatnya terlebih dahulu, maka penyerang dapat menipu sistem pembuktian – inilah mengapa sistem pembuktiannya harus acak. Namun ini juga berarti bahwa koordinat harus diambil dari kumpulan yang cukup besar sehingga penyerang tidak dapat menebaknya secara acak. Hal ini jelas benar jika modulusnya mendekati 2 pangkat 256. Namun, untuk modulus 2^64 – 2^32 + 1, kita belum sampai ke sana, dan hal ini tentunya tidak akan terjadi jika kita turun ke 2^31 – 1. Seorang penyerang mempunyai kemampuan untuk mencoba memalsukan bukti dua miliar kali hingga seseorang beruntung.

Untuk mencegah hal ini, kami mengambil sampel r dari bidang yang diperluas, sehingga, misalnya, Anda dapat mendefinisikan y di mana y^3 = 5, dan mengambil kombinasi 1, y, dan y^2. Ini menjadikan jumlah total koordinat menjadi sekitar 2^93. Sebagian besar polinomial yang dihitung oleh peribahasa tidak termasuk dalam bidang yang diperluas ini; itu hanya bilangan bulat modulo 2^31-1, jadi Anda tetap mendapatkan semua efisiensi dengan menggunakan bidang kecil. Namun pemeriksaan titik acak dan perhitungan FRI menjangkau bidang yang lebih besar ini untuk mendapatkan keamanan yang mereka butuhkan.

Dari bilangan prima kecil hingga bilangan biner

Komputer melakukan aritmatika dengan merepresentasikan bilangan yang lebih besar sebagai rangkaian 0 dan 1, dan membangun sirkuit di atas bit tersebut untuk menghitung operasi seperti penjumlahan dan perkalian. Komputer secara khusus dioptimalkan untuk bilangan bulat 16-, 32-, dan 64-bit. Misalnya, 2^64 – 2^32 + 1 dan 2^31 – 1 dipilih bukan hanya karena memenuhi batasan tersebut, namun juga karena memenuhi batasan tersebut: modul perkalian 2^64 – 2^32 + 1 dapat dilakukan dengan melakukan perkalian 32-bit biasa, dan menggeser secara bitwise serta menyalin keluaran di beberapa tempat; artikel ini menjelaskan beberapa trik dengan baik.

Namun, pendekatan yang jauh lebih baik adalah dengan melakukan penghitungan secara langsung dalam biner. Bagaimana jika penjumlahan dapat dilakukan hanya dengan XOR, tanpa harus khawatir mengenai carryover dari penambahan 1 + 1 dari satu bit ke bit berikutnya? Bagaimana jika perkalian bisa diparalelkan dengan cara yang sama? Semua keunggulan ini didasarkan pada kemampuan merepresentasikan nilai benar/salah dengan satu bit.

Mendapatkan keuntungan dari melakukan komputasi biner secara langsung adalah hal yang coba dilakukan Binius. Tim Binius mendemonstrasikan peningkatan efisiensi dalam presentasi mereka di zkSummit:

Meskipun ukurannya kira-kira sama, operasi pada bidang biner 32-bit memerlukan sumber daya komputasi 5 kali lebih sedikit dibandingkan operasi pada bidang Mersenne 31-bit.

Dari polinomial univariat hingga hypercubes

Misalkan kita mempercayai alasan ini, dan ingin melakukan semuanya dengan bit (0 dan 1). Bagaimana kita bisa merepresentasikan satu miliar bit dengan satu polinomial?

Di sini kita menghadapi dua masalah praktis:

1. Agar polinomial mewakili sejumlah besar nilai, nilai-nilai ini harus dapat diakses ketika mengevaluasi polinomial: dalam contoh Fibonacci di atas, F(0), F(1) … F(100), dan dalam perhitungan yang lebih besar , eksponennya akan mencapai jutaan. Bidang yang kita gunakan harus berisi angka sebesar ini.

2. Membuktikan nilai apa pun yang kita masukkan dalam pohon Merkle (seperti semua STARK) memerlukan pengkodean Reed-Solomon: misalnya, memperluas nilai dari n ke 8n, menggunakan redundansi untuk mencegah pembukti jahat berbuat curang dengan memalsukan nilai selama penghitungan. Hal ini juga memerlukan bidang yang cukup besar: untuk memperluas dari satu juta nilai menjadi 8 juta, Anda memerlukan 8 juta titik berbeda untuk mengevaluasi polinomial.

Ide utama Binius adalah menyelesaikan dua masalah ini secara terpisah, dan melakukannya dengan merepresentasikan data yang sama dalam dua cara berbeda. Pertama, polinomial itu sendiri. Sistem seperti SNARK berbasis kurva elips, STARK era 2019, Plonky 2, dan lainnya biasanya menangani polinomial pada satu variabel: F(x). Binius, sebaliknya, mengambil inspirasi dari protokol Spartan dan menggunakan polinomial multivariat: F(x 1, x 2,… xk). Akibatnya, kita mewakili seluruh lintasan komputasi pada komputasi hypercube, di mana masing-masing xi adalah 0 atau 1. Misalnya, jika kita ingin mewakili deret Fibonacci, dan kita masih menggunakan bidang yang cukup besar untuk mewakilinya, kita bisa bayangkan 16 urutan pertama mereka seperti ini: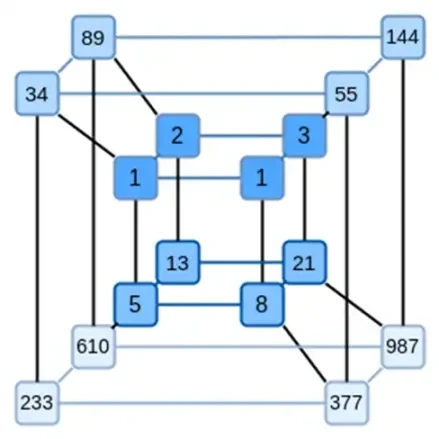

Artinya, F(0,0,0,0) harusnya 1, F(1,0,0,0) juga 1, F(0,1,0,0) adalah 2, dan seterusnya, semua hingga F(1,1,1,1) = 987. Mengingat komputasi hypercube, terdapat polinomial linier multivariat (derajat 1 di setiap variabel) yang menghasilkan komputasi ini. Jadi kita dapat menganggap kumpulan nilai ini mewakili polinomial; kita tidak perlu menghitung koefisiennya.

Contoh ini tentu saja hanya sebagai ilustrasi: dalam praktiknya, inti dari masuk ke hypercube adalah membiarkan kita menangani bit-bit individual. Cara asli Binius untuk menghitung bilangan Fibonacci adalah dengan menggunakan kubus berdimensi lebih tinggi, menyimpan satu bilangan per kelompok, katakanlah, 16 bit. Hal ini memerlukan kecerdikan untuk mengimplementasikan penjumlahan bilangan bulat secara bit, tetapi bagi Binius, ini tidak terlalu sulit.

Sekarang, mari kita lihat kode penghapusan. Cara kerja STARK adalah Anda mengambil n nilai, Reed-Solomon memperluasnya ke lebih banyak nilai (biasanya 8n, biasanya antara 2n dan 32n), lalu secara acak memilih beberapa cabang Merkle dari perluasan dan melakukan semacam pemeriksaan terhadapnya. Hypercube memiliki panjang 2 di setiap dimensi. Oleh karena itu, tidak praktis untuk mengembangkannya secara langsung: tidak ada cukup ruang untuk mengambil sampel cabang Merkle dari 16 nilai. jadi bagaimana kita melakukannya? Anggaplah hypercube itu persegi!

Binius Sederhana – Sebuah Contoh

Melihat Di Sini untuk implementasi protokol python.

Mari kita lihat sebuah contoh, menggunakan bilangan bulat biasa sebagai field untuk kenyamanan (dalam implementasi nyata, kita akan menggunakan elemen field biner). Pertama, kita mengkodekan hypercube yang ingin kita kirimkan sebagai persegi:

Sekarang, kita memperluas persegi menggunakan metode Reed-Solomon. Artinya, kita memperlakukan setiap baris sebagai polinomial derajat 3 yang dievaluasi pada x = { 0, 1, 2, 3 } dan mengevaluasi polinomial yang sama di x = { 4, 5, 6, 7 }: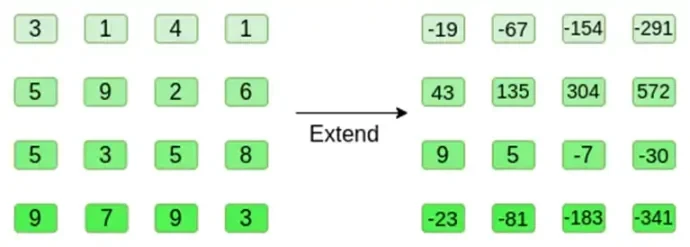

Perhatikan bahwa jumlahnya bisa menjadi sangat besar! Inilah sebabnya mengapa dalam implementasi praktis kita selalu menggunakan bidang berhingga, bukan bilangan bulat biasa: jika kita menggunakan bilangan bulat modulo 11, misalnya, perluasan baris pertama hanya akan menjadi [3, 10, 0, 6].

Jika Anda ingin mencoba ekstensi dan memverifikasi sendiri nomornya, Anda dapat menggunakan kode ekstensi Reed-Solomon sederhana saya di sini.

Selanjutnya, kita memperlakukan ekstensi ini sebagai kolom dan membuat pohon Merkle dari kolom tersebut. Akar pohon Merkle adalah komitmen kami.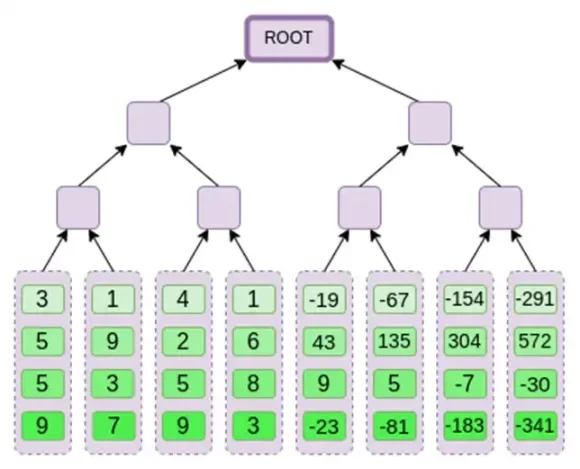

Sekarang, mari kita asumsikan bahwa pembuktian ingin membuktikan perhitungan polinomial r = {r 0, r 1, r 2, r 3 } pada suatu saat. Ada perbedaan halus dalam Binius yang membuatnya lebih lemah dibandingkan skema komitmen polinomial lainnya: pembuktian tidak boleh mengetahui atau dapat menebak s sebelum melakukan ke akar Merkle (dengan kata lain, r harus berupa nilai pseudo-acak yang bergantung pada akar Merkle). Hal ini membuat skema tidak berguna untuk pencarian database (misalnya, oke, Anda memberi saya root Merkle, sekarang buktikan kepada saya P(0, 0, 1, 0)!). Namun protokol tanpa pengetahuan yang sebenarnya kami gunakan biasanya tidak memerlukan pencarian basis data; mereka hanya perlu memeriksa polinomial pada titik evaluasi acak. Jadi pembatasan ini bermanfaat bagi tujuan kami.

Misalkan kita memilih r = { 1, 2, 3, 4 } (polinomialnya bernilai -137; Anda dapat mengonfirmasinya menggunakan kode ini). Sekarang, kita sampai pada buktinya. Kita membagi r menjadi dua bagian: bagian pertama { 1, 2 } mewakili kombinasi linier kolom-kolom dalam baris, dan bagian kedua { 3, 4 } mewakili kombinasi linier baris-baris tersebut. Kami menghitung produk tensor dan untuk kolom:

Untuk bagian baris:

Artinya: daftar semua produk yang mungkin dari suatu nilai di setiap himpunan. Dalam kasus baris, kita mendapatkan:

[( 1-r 2)*( 1-r 3), ( 1-r 3), ( 1-r 2)*r 3, r 2*r 3 ]

Dengan r = { 1, 2, 3, 4 } (jadi r 2 = 3 dan r 3 = 4):

[( 1-3)*( 1-4), 3*( 1-4),( 1-3)* 4, 3* 4 ] = [ 6, -9 -8 -12 ]

Sekarang, kita menghitung baris baru t dengan mengambil kombinasi linier dari baris yang ada. Artinya, kami mengambil:

Anda dapat menganggap apa yang terjadi di sini sebagai evaluasi parsial. Jika kita mengalikan hasil kali tensor penuh dengan vektor penuh semua nilai, Anda akan mendapatkan perhitungan P(1, 2, 3, 4) = -137. Di sini, kita telah mengalikan hasil kali tensor parsial hanya dengan menggunakan setengah koordinat evaluasi, dan mengurangi kisi-kisi nilai N menjadi satu baris nilai akar kuadrat N. Jika Anda memberikan baris ini kepada orang lain, mereka dapat melakukan sisa penghitungan menggunakan hasil kali tensor dari separuh koordinat evaluasi lainnya.

Pepatah memberikan baris baru berikut kepada pemverifikasi: t dan bukti Merkle dari beberapa kolom yang diambil sampelnya secara acak. Dalam contoh ilustratif kita, kita akan meminta pembuktian hanya menyediakan kolom terakhir; dalam kehidupan nyata, pembuktian perlu menyediakan lusinan kolom untuk mencapai keamanan yang memadai.

Sekarang, kita mengeksploitasi linearitas kode Reed-Solomon. Properti utama yang kami eksploitasi adalah bahwa mengambil kombinasi linier dari ekspansi Reed-Solomon memberikan hasil yang sama dengan mengambil ekspansi Reed-Solomon dari kombinasi linier. Independensi sekuensial ini biasanya terjadi ketika kedua operasi bersifat linier.

Verifikator melakukan hal itu. Mereka menghitung t, dan menghitung kombinasi linier dari kolom yang sama yang telah dihitung sebelumnya (tetapi hanya kolom yang disediakan oleh pembukti), dan memverifikasi bahwa kedua prosedur memberikan jawaban yang sama.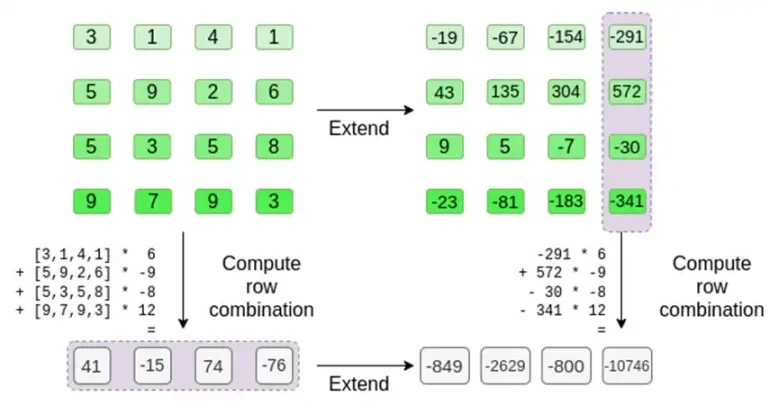

Dalam kasus ini, kita memperluas t dan menghitung kombinasi linier yang sama ([6,-9,-8, 12]), yang keduanya memberikan jawaban yang sama: -10746. Hal ini membuktikan bahwa akar Merkle dibangun dengan itikad baik (atau setidaknya cukup dekat), dan cocok dengan t: setidaknya sebagian besar kolom kompatibel satu sama lain.

Namun ada satu hal lagi yang perlu diperiksa oleh verifikator: memeriksa evaluasi polinomial {r 0 …r 3 }. Semua langkah verifikator selama ini sebenarnya tidak bergantung pada nilai yang diklaim oleh provertif. Inilah cara kami memeriksanya. Kita ambil hasil kali tensor dari “bagian kolom” yang kita tandai sebagai titik komputasi: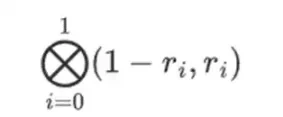

Dalam kasus kita, dimana r = { 1, 2, 3, 4 } sehingga separuh kolom yang dipilih adalah { 1, 2 }), ini setara dengan:

Sekarang kita ambil kombinasi linier t:

Ini sama dengan menyelesaikan polinomial secara langsung.

Di atas sangat dekat dengan penjelasan lengkap tentang protokol Binius sederhana. Hal ini mempunyai beberapa keuntungan menarik: misalnya, karena data dipisahkan menjadi baris dan kolom, Anda hanya memerlukan bidang yang berukuran setengahnya. Namun, hal ini tidak memberikan manfaat penuh dari komputasi biner. Untuk itu, kita memerlukan protokol Binius yang lengkap. Namun pertama-tama, mari kita lihat lebih dalam bidang biner.

Bidang Biner

Bidang terkecil yang mungkin adalah modulo aritmatika 2, yang sangat kecil sehingga kita dapat menulis tabel penjumlahan dan perkalian untuk bidang tersebut:

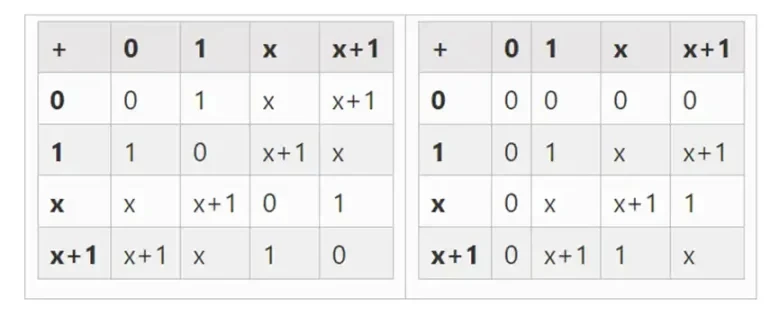
Kita bisa mendapatkan bidang biner yang lebih besar dengan ekstensi: jika kita mulai dengan F 2 (bilangan bulat modulo 2) dan kemudian mendefinisikan x dimana x kuadrat = x + 1 , kita mendapatkan tabel penjumlahan dan perkalian berikut:

Ternyata kita dapat memperluas bidang biner ke ukuran besar dengan mengulangi konstruksi ini. Tidak seperti bilangan kompleks di atas bilangan real, di mana Anda dapat menambahkan elemen baru tetapi tidak pernah menambahkan elemen I lagi (angka empat memang ada, tetapi secara matematis aneh, misalnya ab tidak sama dengan ba), dengan bidang berhingga Anda dapat menambahkan ekstensi baru selamanya. Secara khusus, definisi kami tentang suatu elemen adalah sebagai berikut: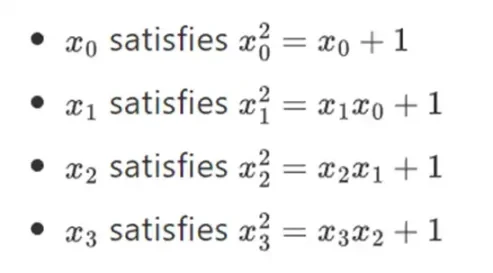

Dan seterusnya… Hal ini sering disebut konstruksi menara, karena setiap perluasan yang berurutan dapat dianggap seperti penambahan lapisan baru pada menara. Ini bukan satu-satunya cara untuk membangun bidang biner dengan ukuran sewenang-wenang, namun memiliki beberapa keunggulan unik yang dieksploitasi Binius.

Kita dapat merepresentasikan angka-angka ini sebagai daftar bit. Misalnya, 1100101010001111. Bit pertama mewakili kelipatan 1, bit kedua mewakili kelipatan x0, dan bit berikutnya mewakili kelipatan x1: x1, x1*x0, x2, x2*x0, dan seterusnya. Pengkodean ini bagus karena Anda dapat memecahnya:

Ini adalah notasi yang relatif jarang, tapi saya suka merepresentasikan elemen bidang biner sebagai bilangan bulat, dengan bit yang lebih efisien di sebelah kanan. Artinya, 1 = 1, x0 = 01 = 2, 1+x0 = 11 = 3, 1+x0+x2 = 11001000 = 19, dan seterusnya. Dalam representasi ini, itu adalah 61779.

Penjumlahan di bidang biner hanyalah XOR (begitu juga dengan pengurangan); perhatikan bahwa ini berarti x+x = 0 untuk sembarang x. Untuk mengalikan dua elemen x*y, ada algoritma rekursif yang sangat sederhana: bagi setiap angka menjadi dua:

Kemudian, bagi perkaliannya:

Bagian terakhir adalah satu-satunya yang sedikit rumit, karena Anda harus menerapkan aturan penyederhanaan. Ada cara yang lebih efisien untuk melakukan perkalian, mirip dengan algoritma Karatsuba dan Fast Fourier Transforms, namun saya akan membiarkannya sebagai latihan agar pembaca yang tertarik dapat mengetahuinya.

Pembagian dalam bidang biner dilakukan dengan menggabungkan perkalian dan inversi. Metode inversi yang sederhana namun lambat adalah penerapan teorema kecil Fermats yang digeneralisasi. Ada juga algoritma inversi yang lebih kompleks namun lebih efisien yang dapat Anda temukan di sini. Anda dapat menggunakan kode di sini untuk bermain-main dengan penjumlahan, perkalian, dan pembagian bidang biner.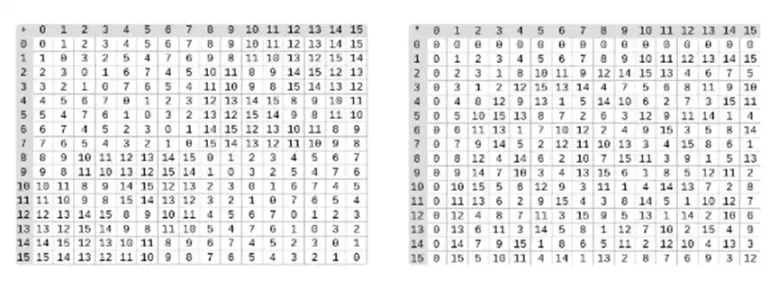

Kiri: Tabel penjumlahan untuk elemen bidang biner empat-bit (yaitu, hanya 1, x 0, x 1, x 0x 1). Kanan: Tabel perkalian untuk elemen bidang biner empat-bit.

Keunggulan bidang biner jenis ini adalah ia menggabungkan beberapa bagian terbaik dari bilangan bulat reguler dan aritmatika modular. Seperti bilangan bulat biasa, elemen bidang biner tidak dibatasi: Anda dapat tumbuh sebesar yang Anda inginkan. Namun seperti aritmatika modular, jika Anda mengoperasikan nilai dalam batas ukuran tertentu, semua hasil Anda akan tetap berada dalam rentang yang sama. Misalnya, jika Anda mengambil 42 pangkat berturut-turut, Anda mendapatkan:

Setelah 255 langkah, Anda kembali ke 42 pangkat 255 = 1, dan seperti bilangan bulat positif dan operasi modular, keduanya mematuhi hukum matematika biasa: a*b=b*a, a*(b+c)= a*b+a*c, dan bahkan beberapa undang-undang baru yang aneh.

Terakhir, bidang biner berguna untuk memanipulasi bit: jika Anda menghitung dengan angka yang sesuai dengan 2k bit, maka semua keluaran Anda akan sesuai dengan 2k bit juga. Hal ini untuk menghindari kecanggungan. Di Ethereums EIP-4844, masing-masing blok blob harus berupa angka modulo 52435875175126190479447740508185965837690552500527637822603658699938581184513, jadi pengkodean data biner memerlukan membuang beberapa ruang dan melakukan pemeriksaan ekstra pada lapisan aplikasi untuk memastikannya nilai yang disimpan di setiap elemen kurang dari 2248. Ini juga berarti bahwa operasi bidang biner berjalan sangat cepat di komputer – baik CPU maupun desain FPGA dan ASIC yang secara teoritis optimal.

Ini semua berarti bahwa kita dapat melakukan pengkodean Reed-Solomon seperti yang kita lakukan di atas, dengan cara yang benar-benar menghindari ledakan bilangan bulat seperti yang kita lihat dalam contoh kita, dan dengan cara yang sangat asli, jenis komputasi yang dapat dilakukan dengan baik oleh komputer. Properti pemisahan bidang biner – bagaimana kita dapat melakukan 1100101010001111 = 11001010 + 10001111*x 3 , dan kemudian membaginya sesuai kebutuhan – juga penting untuk memberikan banyak fleksibilitas.

Binius Lengkap

Melihat Di Sini untuk implementasi protokol python.

Sekarang kita dapat beralih ke “Binius penuh,” yang mengadaptasi “Binius sederhana” untuk (i) bekerja pada bidang biner dan (ii) mari kita melakukan komitmen bit tunggal. Protokol ini sulit untuk dipahami karena ia beralih bolak-balik antara berbagai cara dalam memandang matriks bit; tentu saja saya memerlukan waktu lebih lama untuk memahaminya daripada biasanya saya memerlukan waktu untuk memahami protokol kriptografi. Namun begitu Anda memahami bidang biner, kabar baiknya adalah “matematika yang lebih sulit” yang diandalkan Binius tidak ada. Ini bukan pasangan kurva elips, di mana terdapat lubang kelinci geometri aljabar yang semakin dalam untuk diturunkan; di sini, Anda hanya memiliki bidang biner.

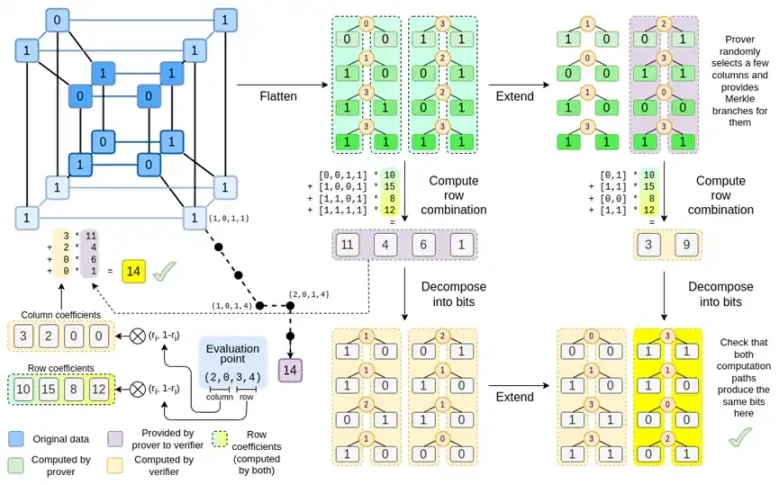
Mari kita lihat kembali grafik selengkapnya:

Saat ini, Anda seharusnya sudah familiar dengan sebagian besar komponennya. Ide untuk meratakan hypercube menjadi grid, ide menghitung kombinasi baris dan kolom sebagai produk tensor titik evaluasi, dan ide memeriksa kesetaraan antara ekspansi Reed-Solomon kemudian menghitung kombinasi baris dan menghitung kombinasi baris kemudian ekspansi Reed-Solomon semuanya diimplementasikan di Binius biasa.

Apa yang baru di Binius Lengkap? Pada dasarnya tiga hal:

• Nilai individual dalam hypercube dan persegi harus berupa bit (0 atau 1).

• Proses perluasan memperluas bit-bit menjadi lebih banyak bit dengan mengelompokkannya ke dalam kolom-kolom dan untuk sementara mengasumsikan bahwa bit-bit tersebut adalah elemen dari bidang yang lebih besar.

• Setelah langkah kombinasi baris, ada dekomposisi elemen menjadi langkah bit yang mengubah ekspansi kembali menjadi bit.

Kami akan membahas kedua kasus tersebut secara bergantian. Pertama, prosedur perpanjangan baru. Kode Reed-Solomon memiliki batasan mendasar, jika Anda ingin memperluas n ke k*n, Anda harus bekerja di bidang dengan k*n nilai berbeda yang dapat digunakan sebagai koordinat. Dengan F 2 (alias bit), Anda tidak bisa melakukan itu. Jadi yang kita lakukan adalah menyatukan elemen-elemen F 2 yang berdekatan untuk membentuk nilai yang lebih besar. Dalam contoh di sini, kita mengemas dua bit sekaligus ke dalam elemen { 0 , 1 , 2 , 3 } , yang cukup bagi kita karena ekstensi kita hanya memiliki empat titik komputasi. Sebagai bukti nyata, kita mungkin kembali ke 16 bit sekaligus. Kami kemudian mengeksekusi kode Reed-Solomon pada nilai-nilai yang dikemas ini dan membongkarnya menjadi beberapa bit lagi.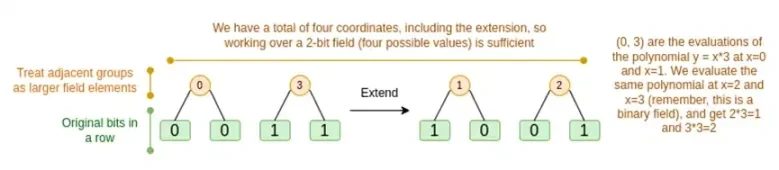

Sekarang, kombinasi baris. Untuk membuat evaluasi pada pemeriksaan titik acak aman secara kriptografis, kita perlu mengambil sampel titik tersebut dari ruang yang cukup besar (jauh lebih besar daripada hypercube itu sendiri). Jadi meskipun titik di dalam hypercube adalah bit, nilai yang dihitung di luar hypercube akan jauh lebih besar. Pada contoh di atas, kombinasi barisnya menjadi [11, 4, 6, 1].

Hal ini menimbulkan masalah: kita mengetahui cara mengelompokkan bit ke dalam nilai yang lebih besar dan kemudian melakukan ekspansi Reed-Solomon pada nilai tersebut, namun bagaimana kita melakukan hal yang sama untuk pasangan nilai yang lebih besar?

Trik Binius adalah melakukannya sedikit demi sedikit: kita melihat satu bit dari setiap nilai (misalnya, untuk benda yang kita beri label 11, yaitu [1, 1, 0, 1]), lalu kita memperluasnya baris demi baris. Artinya, kita memperluasnya pada baris 1 setiap elemen, lalu pada baris x0, lalu pada baris x1, lalu pada baris x0x1, dan seterusnya (nah, dalam contoh mainan kita, kita berhenti di situ, tetapi dalam contoh nyata implementasi kita akan naik menjadi 128 baris (yang terakhir adalah x6*…*x0))

tinjauan:

• Kami mengubah bit di hypercube menjadi grid

• Kami kemudian memperlakukan kelompok bit yang berdekatan pada setiap baris sebagai elemen bidang yang lebih besar dan melakukan operasi aritmatika pada bit tersebut untuk Reed-Solomon memperluas baris

• Kami kemudian mengambil kombinasi baris setiap kolom bit dan mendapatkan kolom bit untuk setiap baris sebagai keluaran (jauh lebih kecil untuk kotak yang lebih besar dari 4 x 4)

• Kemudian, kita menganggap keluarannya sebagai matriks dan bit-bitnya sebagai baris

Mengapa ini terjadi? Dalam matematika normal, jika Anda mulai mengiris angka sedikit demi sedikit, kemampuan (biasanya) untuk melakukan operasi linier dalam urutan apa pun dan mendapatkan hasil yang sama akan terganggu. Misalnya, jika saya memulai dengan angka 345, dan mengalikannya dengan 8, lalu dengan 3, saya mendapatkan 8280, dan jika saya melakukan kedua operasi tersebut secara terbalik, saya juga mendapatkan 8280. Tetapi jika saya memasukkan operasi pengirisan bit di antara dua langkah tersebut, hasilnya rusak: jika Anda melakukan 8x, lalu 3x, Anda mendapatkan: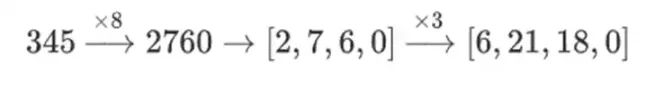

Tetapi jika Anda melakukannya 3x, lalu 8x, Anda mendapatkan:

Namun dalam bidang biner yang dibangun dengan struktur menara, pendekatan ini berhasil. Alasannya adalah keterpisahannya: jika Anda mengalikan nilai yang besar dengan nilai yang kecil, apa yang terjadi pada setiap segmen akan tetap pada setiap segmen. Jika 1100101010001111 dikalikan dengan 11, maka hasilnya sama dengan hasil penguraian pertama dari 1100101010001111, yaitu

Kemudian kalikan setiap komponen dengan 11.

Menyatukan semuanya

Secara umum, sistem pembuktian tanpa pengetahuan bekerja dengan membuat pernyataan tentang polinomial yang mewakili pernyataan tentang evaluasi yang mendasarinya pada saat yang sama: seperti yang kita lihat dalam contoh Fibonacci, F(X+ 2)-F(X+ 1)-F( X) = Z(X)*H(X) sambil memeriksa semua langkah perhitungan Fibonacci. Kami memeriksa pernyataan tentang polinomial dengan membuktikan evaluasi pada titik acak. Pemeriksaan titik acak ini mewakili pemeriksaan seluruh polinomial: jika persamaan polinomial tidak cocok, kecil kemungkinan persamaan tersebut cocok pada koordinat acak tertentu.

Dalam praktiknya, salah satu sumber utama inefisiensi adalah bahwa dalam program nyata, sebagian besar angka yang kita tangani berukuran kecil: indeks dalam perulangan for, nilai Benar/Salah, penghitung, dan sebagainya. Namun, ketika kami memperluas data dengan pengkodean Reed-Solomon untuk menyediakan redundansi yang diperlukan untuk membuat pemeriksaan berbasis bukti Merkle aman, sebagian besar nilai tambahan akhirnya memenuhi seluruh ukuran bidang, meskipun nilai aslinya kecil.

Untuk memperbaikinya, kami ingin membuat bidang ini sekecil mungkin. Plonky 2 membawa kita dari angka 256-bit ke angka 64-bit, dan kemudian Plonky 3 menurunkannya lebih jauh menjadi 31 bit. Namun itu pun belum optimal. Dengan bidang biner, kita dapat menangani bit tunggal. Hal ini membuat pengkodean menjadi padat: jika data dasar aktual Anda memiliki n bit, maka pengkodean Anda akan memiliki n bit, dan perluasannya akan memiliki 8*n bit, tanpa overhead tambahan.

Sekarang, mari kita lihat grafik ini untuk ketiga kalinya:

Di Binius, kami mengerjakan polinomial multilinear: hiperkubus P(x0, x1,…xk) dengan evaluasi tunggal P(0, 0, 0, 0), P(0, 0, 0, 1) hingga P( 1, 1, 1, 1), menyimpan data yang kita pedulikan. Untuk membuktikan perhitungan pada titik tertentu, kami menafsirkan ulang data yang sama sebagai persegi. Kami kemudian memperluas setiap baris, menggunakan pengkodean Reed-Solomon untuk menyediakan redundansi data yang diperlukan untuk keamanan terhadap kueri cabang Merkle yang diacak. Kami kemudian menghitung kombinasi linier acak dari baris-baris tersebut, merancang koefisien sehingga baris gabungan baru benar-benar berisi nilai komputasi yang kami pedulikan. Baris yang baru dibuat ini (ditafsirkan ulang sebagai baris 128-bit) dan beberapa kolom yang dipilih secara acak dengan cabang Merkle diteruskan ke verifikator.

Pemverifikasi kemudian melakukan kombinasi baris yang diperluas (atau lebih tepatnya, kolom yang diperluas) dan kombinasi baris yang diperluas dan memverifikasi bahwa keduanya cocok. Ia kemudian menghitung kombinasi kolom dan memeriksa apakah ia mengembalikan nilai yang diklaim oleh pembukti. Ini adalah sistem pembuktian kami (atau lebih tepatnya, skema komitmen polinomial, yang merupakan komponen kunci dari sistem pembuktian).

Apa yang belum kita bahas?

• Algoritme yang efisien untuk memperluas baris diperlukan agar validator benar-benar efisien secara komputasi. Kami menggunakan Transformasi Fast Fourier pada bidang biner, yang dijelaskan di sini (walaupun implementasi sebenarnya akan berbeda, karena postingan ini menggunakan konstruksi yang kurang efisien yang tidak didasarkan pada ekspansi rekursif).

• Secara hitung. Polinomial univariat mudah digunakan karena Anda dapat melakukan hal-hal seperti F(X+2)-F(X+1)-F(X) = Z(X)*H(X) untuk menghubungkan langkah-langkah yang berdekatan dalam komputasi. Di hypercube, langkah selanjutnya kurang dijelaskan dengan baik dibandingkan X+1. Anda dapat melakukan X+k, pangkat k, tetapi perilaku melompat ini mengorbankan banyak keunggulan utama Binius. Makalah Binius menjelaskan solusinya. Lihat Bagian 4.3), namun hal ini merupakan sebuah lubang kelinci yang dalam.

• Cara melakukan pemeriksaan nilai tertentu dengan aman. Contoh Fibonacci memerlukan pemeriksaan kondisi batas utama: nilai F(0)=F(1)=1 dan F(100). Namun untuk Binius asli, tidak aman untuk melakukan pemeriksaan pada titik perhitungan yang diketahui. Ada beberapa cara yang cukup sederhana untuk mengubah pemeriksaan perhitungan yang diketahui menjadi pemeriksaan perhitungan yang tidak diketahui, dengan menggunakan apa yang disebut protokol pemeriksaan jumlah; tapi kami tidak akan membahasnya di sini.

• Protokol pencarian, teknologi lain yang banyak digunakan akhir-akhir ini, digunakan untuk membuat sistem pembuktian yang super efisien. Binius dapat digunakan bersama dengan protokol pencarian untuk banyak aplikasi.

• Melampaui waktu verifikasi akar kuadrat. Akar kuadrat mahal: bukti Binius 2^32 bit panjangnya sekitar 11 MB. Anda dapat mengimbanginya dengan menggunakan sistem pembuktian lain untuk membuat pembuktian pembuktian Binius, sehingga memberi Anda efisiensi pembuktian Binius dengan ukuran pembuktian yang lebih kecil. Pilihan lainnya adalah protokol FRI-Binius yang lebih kompleks, yang menghasilkan bukti ukuran multi-logaritmik (seperti FRI biasa).

• Bagaimana Binius memengaruhi keramahan terhadap SNARK. Ringkasan dasarnya adalah jika Anda menggunakan Binius, Anda tidak perlu lagi membuat perhitungan ramah aritmatika: hashing biasa tidak lagi lebih efisien daripada hashing aritmatika tradisional, perkalian modulo 2 pangkat 32 atau modulo 2 pangkat 256 tidak lagi sesakit perkalian modulo 2, dan seterusnya. Tapi ini adalah topik yang kompleks. Banyak hal berubah ketika semuanya dilakukan dalam biner.

Saya berharap untuk melihat lebih banyak perbaikan dalam teknologi pembuktian berbasis bidang biner dalam beberapa bulan mendatang.

Artikel ini bersumber dari internet: Vitalik: Binius, bukti efisien untuk bidang biner

Terkait: Koin BNB Menunjukkan Tanda-Tanda Pemulihan: Nilai Tertinggi Tahunan Baru Terlihat

Singkatnya, harga BNB bangkit kembali dari $550 hingga mendekati penembusan resistensi $593. Indikator harga telah mendapatkan kembali momentum bullish, yang mendukung kenaikan 8%. Rasio Sharpe di 4.03 kemungkinan akan mendorong investor baru menuju token pertukaran. Maret adalah bulan yang menguntungkan bagi BNB Coin, dengan mata uang kripto ini mencapai dua level tertinggi baru untuk tahun ini hanya dalam beberapa hari sebelum mengalami koreksi. Setelah periode pemulihan hampir dua minggu, BNB Coin menunjukkan tanda-tanda potensi mencapai titik tertinggi baru pada tahun 2024. Namun apakah pencapaian tersebut dapat dicapai? BNB Tampak Menjanjikan Setelah rebound dari level dukungan $550, nilai BNB Coin telah meningkat menjadi $581 pada saat analisis ini dibuat. Peningkatan ini mencerminkan pemulihan profil pengembalian risiko altcoin,…