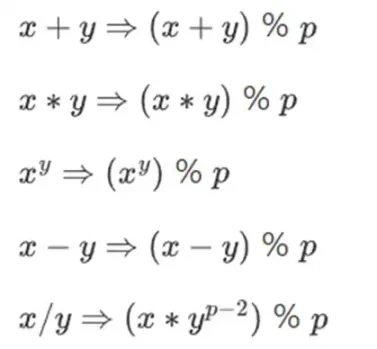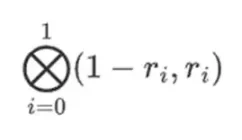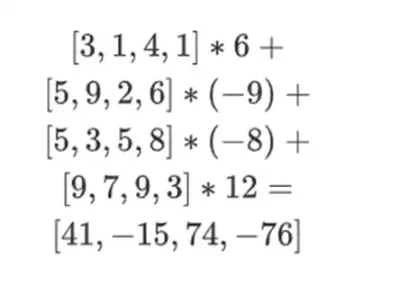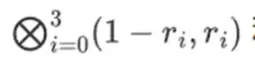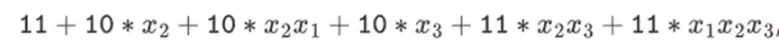विटालिक: बिनियस, बाइनरी क्षेत्रों के लिए कुशल प्रमाण

मूल लेख: विटालिक ब्यूटेरिन

मूल अनुवाद: केट, मार्सबिट

यह पोस्ट मुख्य रूप से उन पाठकों के लिए है जो 2019-युग की क्रिप्टोग्राफी और विशेष रूप से SNARKs और STARKs से परिचित हैं। यदि आप नहीं हैं, तो मेरा सुझाव है कि आप पहले उन्हें पढ़ें। जस्टिन ड्रेक, जिम पोसेन, बेंजामिन डायमंड और रेडी कोजबेसिक को उनकी प्रतिक्रिया और टिप्पणियों के लिए विशेष धन्यवाद।

Over the past two years, STARKs have become a key and irreplaceable technology for efficiently making easily verifiable cryptographic proofs of very complex statements (e.g. proving that an Ethereum block is valid). One of the key reasons for this is the small field size: SNARKs based on elliptic curves require you to work on 256-bit integers to be secure enough, while STARKs allow you to use much smaller field sizes with greater efficiency: first the Goldilocks field (64-bit integer), then Mersenne 31 and BabyBear (both 31 bits). Due to these efficiency gains, Plonky 2 using Goldilocks is hundreds of times faster than its predecessors at proving many kinds of computations.

एक स्वाभाविक प्रश्न यह है: क्या हम इस प्रवृत्ति को इसके तार्किक निष्कर्ष तक ले जा सकते हैं और ऐसे प्रमाण सिस्टम बना सकते हैं जो सीधे शून्य और एक पर काम करके तेज़ी से चलते हैं? यह वही है जो बिनियस करने का प्रयास करता है, कई गणितीय तरकीबों का उपयोग करके जो इसे तीन साल पहले के SNARKs और STARKs से बहुत अलग बनाती हैं। यह पोस्ट बताती है कि छोटे क्षेत्र प्रमाण निर्माण को अधिक कुशल क्यों बनाते हैं, बाइनरी फ़ील्ड अद्वितीय रूप से शक्तिशाली क्यों हैं, और बाइनरी फ़ील्ड पर प्रमाणों को इतना कुशल बनाने के लिए बिनियस द्वारा उपयोग की जाने वाली तरकीबें।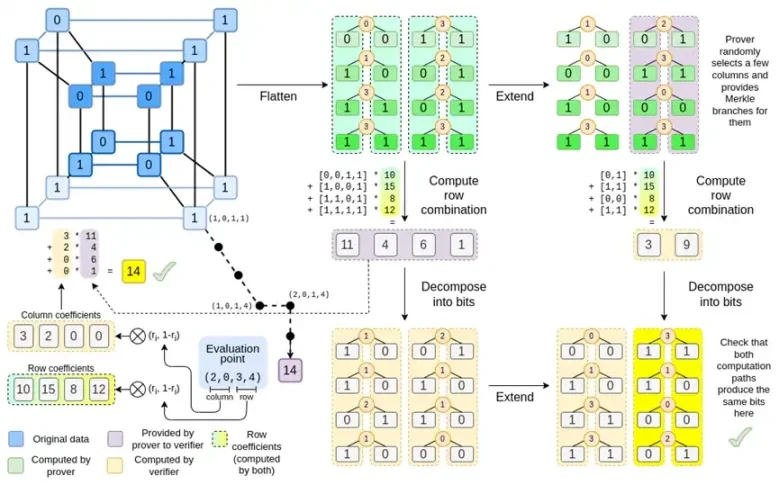

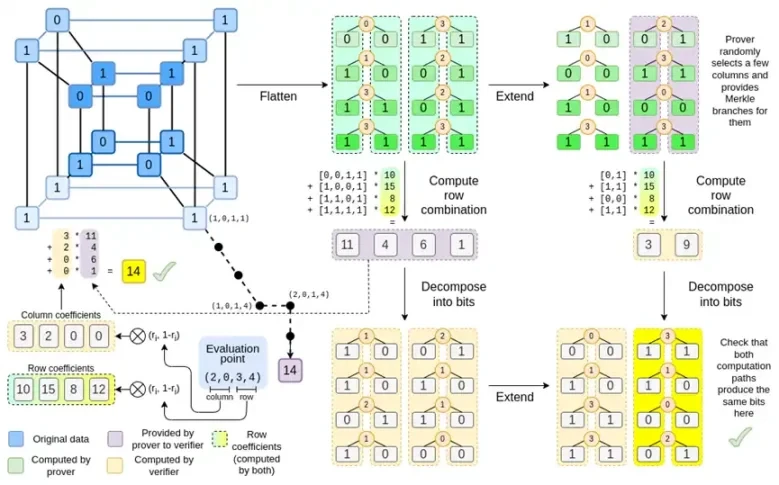
बिनियस, इस पोस्ट के अंत तक आप इस आरेख के हर भाग को समझने में सक्षम हो जायेंगे।

समीक्षा: परिमित क्षेत्र

क्रिप्टोग्राफ़िक प्रूफ़ सिस्टम का एक मुख्य कार्य बड़ी मात्रा में डेटा पर काम करना है, जबकि संख्याओं को छोटा रखना है। यदि आप किसी बड़े प्रोग्राम के बारे में कथन को कुछ संख्याओं वाले गणितीय समीकरण में संक्षिप्त कर सकते हैं, लेकिन वे संख्याएँ मूल प्रोग्राम जितनी ही बड़ी हैं, तो आपको कुछ भी हासिल नहीं हुआ है।

संख्याओं को छोटा रखते हुए जटिल अंकगणित करने के लिए, क्रिप्टोग्राफ़र अक्सर मॉड्यूलर अंकगणित का उपयोग करते हैं। हम एक अभाज्य संख्या मापांक p चुनते हैं। % ऑपरेटर का अर्थ है शेषफल लेना: 15% 7 = 1, 53% 10 = 3, और इसी तरह। (ध्यान दें कि उत्तर हमेशा गैर-ऋणात्मक होता है, इसलिए उदाहरण के लिए -1% 10 = 9)

आपने समय जोड़ने और घटाने के संदर्भ में मॉड्यूलर अंकगणित देखा होगा (उदाहरण के लिए, 9 बजे के 4 घंटे बाद क्या समय है?) लेकिन यहाँ, हम किसी संख्या को केवल मॉड्यूलो में जोड़ या घटा नहीं रहे हैं; हम गुणा, भाग और घातांक भी ले सकते हैं।

हम पुनः परिभाषित करते हैं:

उपरोक्त सभी नियम स्व-संगत हैं। उदाहरण के लिए, यदि p = 7 है, तो:

5 + 3 = 1 (क्योंकि 8% 7 = 1)

1-3 = 5 (क्योंकि -2% 7 = 5)

2* 5 = 3

3/5 = 2

ऐसी संरचनाओं के लिए एक अधिक सामान्य शब्द परिमित क्षेत्र है। परिमित क्षेत्र एक गणितीय संरचना है जो अंकगणित के सामान्य नियमों का पालन करती है, लेकिन जिसमें संभावित मानों की संख्या परिमित होती है, ताकि प्रत्येक मान को एक निश्चित आकार द्वारा दर्शाया जा सके।

मॉड्यूलर अंकगणित (या प्राइम फील्ड) परिमित क्षेत्र का सबसे आम प्रकार है, लेकिन एक और प्रकार है: विस्तार क्षेत्र। आपने एक विस्तार क्षेत्र देखा होगा: जटिल संख्याएँ। हम एक नए तत्व की कल्पना करते हैं और इसे i लेबल करते हैं, और इसके साथ गणित करते हैं: (3i+2)*(2i+4)=6i*i+12i+4i+8=16i+2। हम प्राइम फील्ड के विस्तार के साथ भी ऐसा ही कर सकते हैं। जैसे-जैसे हम छोटे क्षेत्रों से निपटना शुरू करते हैं, प्राइम फील्ड का विस्तार सुरक्षा के लिए तेजी से महत्वपूर्ण होता जाता है, और बाइनरी फील्ड (बिनियस द्वारा उपयोग किए जाने वाले) व्यावहारिक उपयोगिता के लिए पूरी तरह से विस्तार पर निर्भर करते हैं।

समीक्षा: अंकगणितीकरण

SNARKs और STARKs कंप्यूटर प्रोग्राम को अंकगणित के माध्यम से साबित करते हैं: आप जिस प्रोग्राम को साबित करना चाहते हैं, उसके बारे में एक कथन लेते हैं और उसे एक बहुपद से जुड़े गणितीय समीकरण में बदल देते हैं। समीकरण का एक वैध समाधान प्रोग्राम के वैध निष्पादन के अनुरूप होता है।

एक सरल उदाहरण के रूप में, मान लीजिए कि मैंने 100वीं फिबोनाची संख्या की गणना की है और मैं आपको यह साबित करना चाहता हूँ कि यह क्या है। मैं एक बहुपद F बनाता हूँ जो फिबोनाची अनुक्रम को एनकोड करता है: इसलिए F(0)=F(1)=1, F(2)=2, F(3)=3, F(4)=5 और इसी तरह 100 चरणों तक। मुझे साबित करने के लिए जो शर्त चाहिए वह यह है कि F(x+2)=F(x)+F(x+1) पूरी रेंज x={0, 1…98} पर। मैं आपको भागफल देकर समझा सकता हूँ:

जहाँ Z(x) = (x-0) * (x-1) * …(x-98)। अगर मैं यह साबित कर सकता हूँ कि F और H इस समीकरण को संतुष्ट करते हैं, तो F को F(x+ 2)-F(x+ 1)-F(x) को इस सीमा में संतुष्ट करना चाहिए। अगर मैं इसके अतिरिक्त यह सत्यापित करता हूँ कि F के लिए, F(0)=F(1)=1, तो F(100) वास्तव में 100वीं फिबोनाची संख्या होनी चाहिए।

यदि आप कुछ अधिक जटिल साबित करना चाहते हैं, तो आप सरल संबंध F(x+2) = F(x) + F(x+1) को अधिक जटिल समीकरण से बदल देते हैं जो मूल रूप से कहता है कि F(x+1) स्टेट F(x) के साथ वर्चुअल मशीन को आरंभ करने का आउटपुट है, और एक कम्प्यूटेशनल चरण चलाते हैं। आप अधिक चरणों को समायोजित करने के लिए संख्या 100 को एक बड़ी संख्या, उदाहरण के लिए, 100000000 से भी बदल सकते हैं।

सभी SNARK और STARK व्यक्तिगत मानों के बीच बड़ी संख्या में संबंधों को दर्शाने के लिए बहुपदों (और कभी-कभी सदिशों और आव्यूहों) पर सरल समीकरणों का उपयोग करने के विचार पर आधारित हैं। सभी एल्गोरिदम ऊपर बताए गए जैसे आसन्न कम्प्यूटेशनल चरणों के बीच समानता की जांच नहीं करते हैं: उदाहरण के लिए, PLONK ऐसा नहीं करता है, और न ही R1CS करता है। लेकिन कई सबसे प्रभावी जाँचें ऐसा करती हैं, क्योंकि एक ही जाँच (या एक ही कुछ जाँच) को कई बार करके ओवरहेड को कम करना आसान होता है।

प्लॉन्की 2: 256-बिट SNARKs और STARKs से 64-बिट तक... केवल STARKs

पाँच साल पहले, शून्य-ज्ञान प्रमाणों के विभिन्न प्रकारों का एक उचित सारांश इस प्रकार था। प्रमाण दो प्रकार के होते हैं: (अण्डाकार वक्र-आधारित) SNARKs और (हैश-आधारित) STARKs। तकनीकी रूप से, STARKs SNARK का एक प्रकार है, लेकिन व्यवहार में, अण्डाकार वक्र-आधारित संस्करण को संदर्भित करने के लिए "SNARK" और हैश-आधारित निर्माण को संदर्भित करने के लिए "STARK" का उपयोग करना आम बात है। SNARKs छोटे होते हैं, इसलिए आप उन्हें बहुत जल्दी सत्यापित कर सकते हैं और उन्हें आसानी से ऑन-चेन इंस्टॉल कर सकते हैं। STARKs बड़े होते हैं, लेकिन उन्हें किसी विश्वसनीय सेटअप की आवश्यकता नहीं होती है, और वे क्वांटम-प्रतिरोधी होते हैं।

STARKs डेटा को बहुपद के रूप में मानकर, उस बहुपद की गणना की गणना करके, तथा विस्तारित डेटा के मर्कल मूल को "बहुपद प्रतिबद्धता" के रूप में उपयोग करके कार्य करते हैं।

यहाँ इतिहास का एक महत्वपूर्ण हिस्सा यह है कि एलिप्टिक कर्व-आधारित SNARK का सबसे पहले व्यापक रूप से उपयोग किया गया था: FRI की बदौलत STARKs 2018 के आसपास तक पर्याप्त रूप से कुशल नहीं बन पाए, और तब तक Zcash एक साल से अधिक समय से चल रहा था। एलिप्टिक कर्व-आधारित SNARK की एक प्रमुख सीमा है: यदि आप एलिप्टिक कर्व-आधारित SNARK का उपयोग करना चाहते हैं, तो इन समीकरणों में अंकगणित एलिप्टिक कर्व पर बिंदुओं की संख्या के मॉड्यूलो के अनुसार किया जाना चाहिए। यह एक बड़ी संख्या है, जो आमतौर पर 2 की घात 256 के करीब होती है: उदाहरण के लिए, bn128 वक्र के लिए यह 21888242871839275222246405745257275088548364400416034343698204186575808495617 है। लेकिन वास्तविक कंप्यूटिंग छोटी संख्याओं का उपयोग करती है: यदि आप अपनी पसंदीदा भाषा में एक वास्तविक प्रोग्राम के बारे में सोचते हैं, तो इसमें उपयोग की जाने वाली अधिकांश चीजें हैं काउंटर, फॉर लूप में इंडेक्स, प्रोग्राम में पोजीशन, सत्य या असत्य को दर्शाने वाले एकल बिट्स, और अन्य चीजें जो लगभग हमेशा केवल कुछ अंकों की होती हैं।

भले ही आपके मूल डेटा में छोटी संख्याएँ हों, प्रूफ़ प्रक्रिया के लिए भागफल, विस्तार, यादृच्छिक रैखिक संयोजन और अन्य डेटा रूपांतरणों की गणना करने की आवश्यकता होती है, जिसके परिणामस्वरूप समान या बड़ी संख्या में ऑब्जेक्ट होंगे जो औसतन आपके फ़ील्ड के पूर्ण आकार के बराबर होंगे। यह एक महत्वपूर्ण अक्षमता पैदा करता है: n छोटे मानों पर गणना को साबित करने के लिए, आपको n बहुत बड़े मानों पर कई और गणनाएँ करनी होंगी। प्रारंभ में, STARKs ने 256-बिट फ़ील्ड का उपयोग करने की SNARK आदत को विरासत में लिया, और इस प्रकार उसी अक्षमता से पीड़ित थे।

कुछ बहुपद मूल्यांकन का रीड-सोलोमन विस्तार। भले ही मूल मान छोटा हो, अतिरिक्त मान फ़ील्ड के पूर्ण आकार तक विस्तारित होते हैं (इस मामले में 2^31 – 1)

2022 में, प्लॉन्की 2 जारी किया गया। प्लॉन्की 2 का मुख्य नवाचार एक छोटी अभाज्य संख्या के मॉड्यूलो के अनुसार अंकगणित करना है: 2 की घात 64 - 2 की घात 32 + 1 = 18446744067414584321। अब, प्रत्येक जोड़ या गुणा हमेशा CPU पर कुछ निर्देशों में किया जा सकता है, और सभी डेटा को एक साथ हैश करना पहले की तुलना में 4 गुना तेज़ है। लेकिन एक समस्या है: यह विधि केवल STARKs के लिए काम करती है। यदि आप SNARKs का उपयोग करने का प्रयास करते हैं, तो ऐसे छोटे अण्डाकार वक्रों के लिए अण्डाकार वक्र असुरक्षित हो जाते हैं।

सुरक्षा सुनिश्चित करने के लिए, प्लॉन्की 2 को एक्सटेंशन फ़ील्ड्स को भी पेश करने की आवश्यकता है। अंकगणितीय समीकरणों की जाँच करने के लिए एक महत्वपूर्ण तकनीक यादृच्छिक बिंदु नमूनाकरण है: यदि आप यह जांचना चाहते हैं कि H(x) * Z(x) F(x+ 2)-F(x+ 1)-F(x) के बराबर है या नहीं, तो आप यादृच्छिक रूप से एक निर्देशांक r चुन सकते हैं, H(r), Z(r), F(r), F(r+ 1) और F(r+ 2) को साबित करने के लिए एक बहुपद प्रतिबद्धता प्रदान कर सकते हैं और फिर सत्यापित कर सकते हैं कि H(r) * Z(r) F(r+ 2)-F(r+ 1)- F(r) के बराबर है या नहीं। यदि कोई हमलावर निर्देशांकों का पहले से अनुमान लगा सकता है, तो हमलावर प्रमाण प्रणाली को धोखा दे सकता है - यही कारण है कि प्रमाण प्रणाली यादृच्छिक होनी चाहिए। लेकिन इसका यह भी अर्थ है कि निर्देशांकों को इतने बड़े सेट से नमूना लिया जाना चाहिए कि हमलावर यादृच्छिक रूप से अनुमान न लगा सके। यह स्पष्ट रूप से सत्य है यदि मापांक 2 की घात 256 के करीब है। हालांकि, मापांक 2^64 – 2^32 + 1 के लिए, हम अभी तक वहां नहीं पहुंचे हैं, और यदि हम 2^31 – 1 तक पहुंच जाते हैं तो यह निश्चित रूप से मामला नहीं है। किसी हमलावर की क्षमता के भीतर दो अरब बार प्रमाण बनाने की कोशिश करना है जब तक कि वह भाग्यशाली न हो जाए।

इसे रोकने के लिए, हम एक विस्तारित क्षेत्र से r का नमूना लेते हैं, ताकि, उदाहरण के लिए, आप y को परिभाषित कर सकें जहाँ y^3 = 5 हो, और 1, y, और y^2 के संयोजन लें। इससे निर्देशांकों की कुल संख्या लगभग 2^93 हो जाती है। प्रूवर द्वारा गणना किए गए अधिकांश बहुपद इस विस्तारित क्षेत्र में नहीं जाते हैं; वे केवल 2^31-1 के मॉड्यूलो पूर्णांक हैं, इसलिए आपको अभी भी एक छोटे क्षेत्र का उपयोग करने से सभी दक्षता मिलती है। लेकिन यादृच्छिक बिंदु जाँच और FRI संगणनाएँ अपनी ज़रूरत की सुरक्षा प्राप्त करने के लिए इस बड़े क्षेत्र में पहुँचती हैं।

छोटी अभाज्य संख्याओं से लेकर बाइनरी संख्याओं तक

कंप्यूटर बड़ी संख्याओं को 0 और 1 के अनुक्रम के रूप में दर्शाकर अंकगणित करते हैं, और उन बिट्स के ऊपर सर्किट बनाकर जोड़ और गुणा जैसे ऑपरेशन की गणना करते हैं। कंप्यूटर विशेष रूप से 16-, 32- और 64-बिट पूर्णांकों के लिए अनुकूलित हैं। उदाहरण के लिए, 2^64 – 2^32 + 1 और 2^31 – 1 को न केवल इसलिए चुना गया क्योंकि वे उन सीमाओं के भीतर फिट होते हैं, बल्कि इसलिए भी क्योंकि वे उन सीमाओं के भीतर अच्छी तरह से फिट होते हैं: 2^64 – 2^32 + 1 के मॉड्यूलो का गुणन नियमित 32-बिट गुणन करके और आउटपुट को कुछ स्थानों पर बिटवाइज़ शिफ्टिंग और कॉपी करके किया जा सकता है; यह लेख कुछ तरकीबों को अच्छी तरह से समझाता है।

हालाँकि, गणनाओं को सीधे बाइनरी में करना ज़्यादा बेहतर तरीका होगा। क्या होगा अगर जोड़ सिर्फ़ XOR हो, एक बिट से दूसरे बिट में 1 + 1 जोड़ने से होने वाले कैरीओवर के बारे में चिंता किए बिना? क्या होगा अगर गुणा को उसी तरह ज़्यादा समानांतर बनाया जा सके? ये सभी फ़ायदे एक बिट के साथ सही/गलत मानों को दर्शाने में सक्षम होने पर आधारित हैं।

बाइनरी कम्प्यूटेशन को सीधे करने के इन लाभों को प्राप्त करना वही है जो बिनियस करने की कोशिश कर रहा है। बिनियस टीम ने zkSummit में अपनी प्रस्तुति में दक्षता लाभ का प्रदर्शन किया:

लगभग समान आकार होने के बावजूद, 32-बिट बाइनरी फ़ील्ड पर संचालन के लिए 31-बिट मर्सेन फ़ील्ड पर संचालन की तुलना में 5 गुना कम कम्प्यूटेशनल संसाधनों की आवश्यकता होती है।

एकचर बहुपद से लेकर हाइपरक्यूब तक

मान लीजिए हम इस तर्क पर विश्वास करते हैं, और सब कुछ बिट्स (0 और 1) के साथ करना चाहते हैं। हम एक अरब बिट्स को एक एकल बहुपद के साथ कैसे दर्शा सकते हैं?

यहां हमें दो व्यावहारिक समस्याओं का सामना करना पड़ता है:

1. किसी बहुपद को बड़ी संख्या में मानों का प्रतिनिधित्व करने के लिए, बहुपद का मूल्यांकन करते समय इन मानों को सुलभ होना चाहिए: ऊपर दिए गए फिबोनाची उदाहरण में, F(0), F(1) … F(100), और एक बड़ी गणना में, घातांक लाखों में होंगे। हमारे द्वारा उपयोग किए जाने वाले फ़ील्ड में इस आकार की संख्याएँ होनी चाहिए।

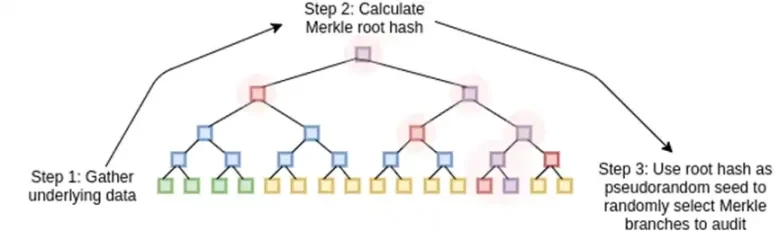
2. मर्कल ट्री (जैसे सभी STARK) में हमारे द्वारा किए गए किसी भी मान को साबित करने के लिए रीड-सोलोमन को इसे एनकोड करने की आवश्यकता होती है: उदाहरण के लिए, n से 8n तक मानों का विस्तार करना, दुर्भावनापूर्ण प्रूवर को गणना के दौरान मान को जाली बनाकर धोखा देने से रोकने के लिए अतिरेक का उपयोग करना। इसके लिए एक बड़े पर्याप्त क्षेत्र की भी आवश्यकता होती है: एक मिलियन मानों से 8 मिलियन तक विस्तार करने के लिए, आपको बहुपद का मूल्यांकन करने के लिए 8 मिलियन अलग-अलग बिंदुओं की आवश्यकता होती है।

बिनियस का एक मुख्य विचार इन दोनों समस्याओं को अलग-अलग हल करना है, और ऐसा एक ही डेटा को दो अलग-अलग तरीकों से दर्शाकर करना है। सबसे पहले, खुद बहुपद। एलिप्टिक कर्व-आधारित SNARKs, 2019-युग STARKs, प्लॉन्की 2 और अन्य जैसी प्रणालियाँ आम तौर पर एक चर पर बहुपदों से निपटती हैं: F(x)। दूसरी ओर, बिनियस स्पार्टन प्रोटोकॉल से प्रेरणा लेता है और बहुभिन्नरूपी बहुपदों का उपयोग करता है: F(x 1, x 2,… xk)। वास्तव में, हम कम्प्यूटेशन के हाइपरक्यूब पर संपूर्ण कम्प्यूटेशनल प्रक्षेप पथ का प्रतिनिधित्व करते हैं, जहाँ प्रत्येक xi या तो 0 या 1 होता है। उदाहरण के लिए, यदि हम एक फिबोनाची अनुक्रम का प्रतिनिधित्व करना चाहते हैं, और हम अभी भी उन्हें दर्शाने के लिए पर्याप्त बड़े क्षेत्र का उपयोग करते हैं, तो हम उनके पहले 16 अनुक्रमों की कल्पना इस तरह कर सकते हैं: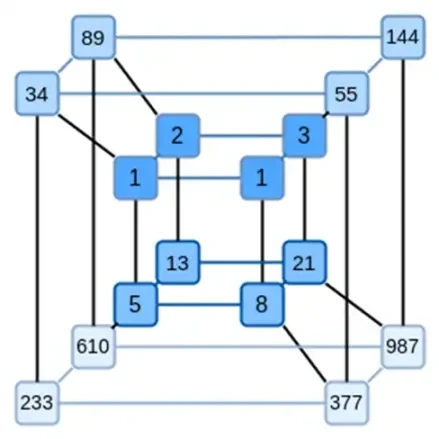

यानी, F(0,0,0,0) 1 होना चाहिए, F(1,0,0,0) भी 1 है, F(0,1,0,0) 2 है, और इसी तरह, F(1,1,1,1) = 987 तक। गणनाओं के ऐसे हाइपरक्यूब को देखते हुए, एक बहुभिन्नरूपी रैखिक (प्रत्येक चर में डिग्री 1) बहुपद है जो इन गणनाओं को उत्पन्न करता है। इसलिए हम मानों के इस सेट को बहुपद का प्रतिनिधित्व करने के रूप में सोच सकते हैं; हमें गुणांकों की गणना करने की आवश्यकता नहीं है।

यह उदाहरण निश्चित रूप से केवल उदाहरण के लिए है: व्यवहार में, हाइपरक्यूब में जाने का पूरा उद्देश्य हमें अलग-अलग बिट्स से निपटने देना है। फिबोनाची संख्याओं की गणना करने का बिनियस-मूल तरीका एक उच्च-आयामी क्यूब का उपयोग करना है, जो 16 बिट्स के प्रत्येक समूह में एक संख्या संग्रहीत करता है। बिट के आधार पर पूर्णांक जोड़ को लागू करने के लिए कुछ चतुराई की आवश्यकता होती है, लेकिन बिनियस के लिए, यह बहुत कठिन नहीं है।

अब, इरेज़र कोड पर नज़र डालते हैं। STARK जिस तरह से काम करता है, वह यह है कि आप n मान लेते हैं, रीड-सोलोमन उन्हें अधिक मानों (आमतौर पर 8n, आमतौर पर 2n और 32n के बीच) तक विस्तारित करते हैं, फिर विस्तार से कुछ मर्कल शाखाओं का यादृच्छिक रूप से चयन करते हैं और उन पर किसी तरह की जाँच करते हैं। हाइपरक्यूब की प्रत्येक आयाम में लंबाई 2 है। इसलिए, इसे सीधे विस्तारित करना व्यावहारिक नहीं है: 16 मानों से मर्कल शाखाओं का नमूना लेने के लिए पर्याप्त जगह नहीं है। तो हम इसे कैसे करते हैं? मान लें कि हाइपरक्यूब एक वर्ग है!

सरल बिनियस – एक उदाहरण

देखना यहाँ प्रोटोकॉल के पायथन कार्यान्वयन के लिए.

आइए एक उदाहरण देखें, सुविधा के लिए नियमित पूर्णांकों को हमारे फ़ील्ड के रूप में उपयोग करते हुए (वास्तविक कार्यान्वयन में, हम बाइनरी फ़ील्ड तत्वों का उपयोग करेंगे)। सबसे पहले, हम हाइपरक्यूब को एनकोड करते हैं जिसे हम एक वर्ग के रूप में प्रस्तुत करना चाहते हैं:

अब, हम रीड-सोलोमन विधि का उपयोग करके वर्ग का विस्तार करते हैं। यानी, हम प्रत्येक पंक्ति को x = { 0, 1, 2, 3 } पर मूल्यांकित 3 डिग्री बहुपद के रूप में मानते हैं और x = { 4, 5, 6, 7 } पर समान बहुपद का मूल्यांकन करते हैं: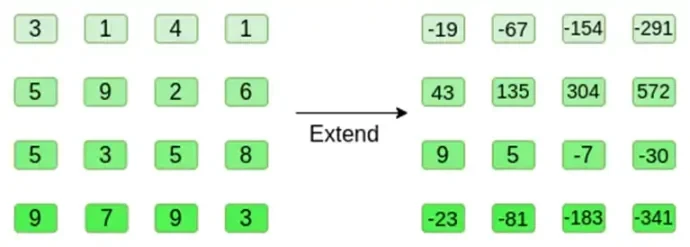

ध्यान दें कि संख्याएँ वास्तव में बड़ी हो सकती हैं! यही कारण है कि व्यावहारिक कार्यान्वयन में हम हमेशा नियमित पूर्णांकों के बजाय परिमित क्षेत्रों का उपयोग करते हैं: यदि हम पूर्णांक मॉड्यूलो 11 का उपयोग करते हैं, उदाहरण के लिए, पहली पंक्ति का विस्तार बस [3, 10, 0, 6] होगा।

यदि आप एक्सटेंशन को आज़माना चाहते हैं और संख्याओं को स्वयं सत्यापित करना चाहते हैं, तो आप यहां मेरे सरल रीड-सोलोमन एक्सटेंशन कोड का उपयोग कर सकते हैं।

इसके बाद, हम इस एक्सटेंशन को एक कॉलम के रूप में देखते हैं और कॉलम का एक मर्कल ट्री बनाते हैं। मर्कल ट्री की जड़ हमारी प्रतिबद्धता है।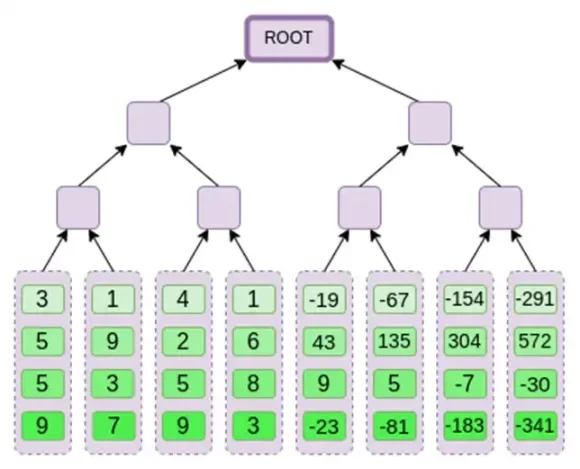

अब, मान लेते हैं कि प्रूवर किसी बिंदु पर इस बहुपद r = {r 0, r 1, r 2, r 3} की गणना को सिद्ध करना चाहता है। बिनियस में एक सूक्ष्म अंतर है जो इसे अन्य बहुपद प्रतिबद्धता योजनाओं की तुलना में कमज़ोर बनाता है: प्रूवर को मर्कल रूट के लिए प्रतिबद्ध होने से पहले s को नहीं जानना चाहिए या अनुमान लगाने में सक्षम नहीं होना चाहिए (दूसरे शब्दों में, r एक छद्म यादृच्छिक मान होना चाहिए जो मर्कल रूट पर निर्भर करता है)। यह डेटाबेस लुकअप के लिए योजना को बेकार बनाता है (उदाहरण के लिए, ठीक है, आपने मुझे मर्कल रूट दिया, अब मुझे P (0, 0, 1, 0) साबित करें!)। लेकिन शून्य-ज्ञान प्रमाण प्रोटोकॉल जो हम वास्तव में उपयोग करते हैं, उन्हें आमतौर पर डेटाबेस लुकअप की आवश्यकता नहीं होती है; उन्हें केवल यादृच्छिक मूल्यांकन बिंदु पर बहुपद की जाँच करने की आवश्यकता होती है। इसलिए यह प्रतिबंध हमारे उद्देश्यों को अच्छी तरह से पूरा करता है।

मान लीजिए कि हम r = { 1, 2, 3, 4 } चुनते हैं (बहुपद का मूल्यांकन -137 होता है; आप इस कोड का उपयोग करके इसकी पुष्टि कर सकते हैं)। अब, हम प्रमाण पर पहुँचते हैं। हम r को दो भागों में विभाजित करते हैं: पहला भाग { 1, 2 } पंक्ति के भीतर स्तंभों के रैखिक संयोजन को दर्शाता है, और दूसरा भाग { 3, 4 } पंक्तियों के रैखिक संयोजन को दर्शाता है। हम स्तंभों के लिए टेंसर उत्पाद की गणना करते हैं:

पंक्ति भाग के लिए:

इसका मतलब है: प्रत्येक सेट में किसी मान के सभी संभावित उत्पादों की सूची। पंक्ति मामले में, हमें मिलता है:

[( 1-आर 2)*( 1-आर 3), ( 1-आर 3), ( 1-आर 2)*आर 3, आर 2*आर 3 ]

r = { 1, 2, 3, 4 } के साथ (अतः r 2 = 3 और r 3 = 4):

[( 1-3)*( 1-4), 3*( 1-4),( 1-3)* 4, 3* 4 ] = [ 6, -9 -8 -12 ]

अब, हम मौजूदा पंक्तियों का रैखिक संयोजन लेकर एक नई पंक्ति t की गणना करते हैं। यानी, हम लेते हैं:

आप यहाँ जो हो रहा है उसे आंशिक मूल्यांकन के रूप में सोच सकते हैं। यदि हम पूर्ण टेंसर उत्पाद को सभी मानों के पूर्ण सदिश से गुणा करते हैं, तो आपको गणना P(1, 2, 3, 4) = -137 प्राप्त होगी। यहाँ, हमने मूल्यांकन निर्देशांक के केवल आधे हिस्से का उपयोग करके आंशिक टेंसर उत्पाद को गुणा किया है, और N मानों के ग्रिड को N मानों के वर्गमूल की एक पंक्ति में घटा दिया है। यदि आप यह पंक्ति किसी और को देते हैं, तो वे मूल्यांकन निर्देशांक के दूसरे आधे हिस्से के टेंसर उत्पाद का उपयोग करके शेष गणना कर सकते हैं।

प्रूवर सत्यापनकर्ता को निम्नलिखित नई पंक्ति प्रदान करता है: t और कुछ यादृच्छिक रूप से नमूना किए गए स्तंभों का मर्कल प्रमाण। हमारे उदाहरणात्मक उदाहरण में, हम प्रूवर को केवल अंतिम स्तंभ प्रदान करने देंगे; वास्तविक जीवन में, प्रूवर को पर्याप्त सुरक्षा प्राप्त करने के लिए दर्जनों स्तंभ प्रदान करने की आवश्यकता होगी।

अब, हम रीड-सोलोमन कोड की रैखिकता का फायदा उठाते हैं। हम जिस मुख्य गुण का फायदा उठाते हैं वह यह है कि रीड-सोलोमन विस्तार का रैखिक संयोजन लेने से वही परिणाम मिलता है जो एक रैखिक संयोजन का रीड-सोलोमन विस्तार लेने से मिलता है। यह अनुक्रमिक स्वतंत्रता आमतौर पर तब होती है जब दोनों ऑपरेशन रैखिक होते हैं।

सत्यापनकर्ता ठीक यही करता है। वे t की गणना करते हैं, और उन्हीं स्तंभों के रैखिक संयोजनों की गणना करते हैं जिन्हें प्रमाणक ने पहले गणना की थी (लेकिन केवल प्रमाणक द्वारा प्रदान किए गए स्तंभ), और सत्यापित करते हैं कि दोनों प्रक्रियाएं एक ही उत्तर देती हैं।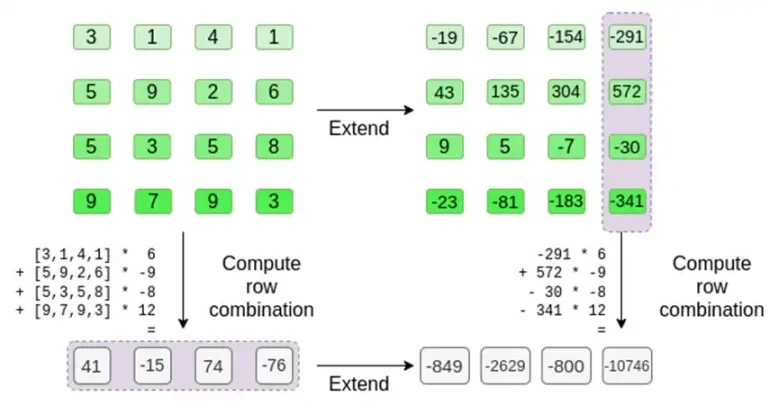

इस मामले में, हम t का विस्तार करते हैं और उसी रैखिक संयोजन ([6,-9,-8, 12]) की गणना करते हैं, जो दोनों एक ही उत्तर देते हैं: -10746। यह साबित करता है कि मर्कल रूट का निर्माण सद्भावना से किया गया था (या कम से कम काफी करीब), और यह t से मेल खाता है: कम से कम अधिकांश कॉलम एक दूसरे के साथ संगत हैं।

लेकिन एक और चीज़ है जिसे सत्यापनकर्ता को जाँचने की ज़रूरत है: बहुपद {r 0 …r 3 } के मूल्यांकन की जाँच करें। सत्यापनकर्ता के अब तक के सभी चरण वास्तव में प्रमाणक द्वारा दावा किए गए मान पर निर्भर नहीं हैं। यहाँ बताया गया है कि हम इसे कैसे जाँचते हैं। हम "कॉलम भाग" का टेंसर उत्पाद लेते हैं जिसे हमने गणना बिंदु के रूप में चिह्नित किया है: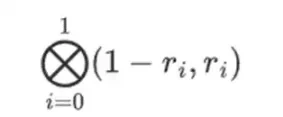

हमारे मामले में, जहाँ r = { 1, 2, 3, 4 } अतः चयनित स्तंभों का आधा भाग { 1, 2 } है), यह इसके समतुल्य है:

अब हम यह रैखिक संयोजन t लेते हैं:

यह बहुपद को सीधे हल करने के समान है।

उपरोक्त सरल बिनियस प्रोटोकॉल के पूर्ण विवरण के बहुत करीब है। इसके पहले से ही कुछ दिलचस्प लाभ हैं: उदाहरण के लिए, चूंकि डेटा पंक्तियों और स्तंभों में विभाजित है, इसलिए आपको केवल आधे आकार के फ़ील्ड की आवश्यकता है। हालाँकि, यह बाइनरी में कंप्यूटिंग के पूर्ण लाभ प्राप्त नहीं करता है। इसके लिए, हमें पूर्ण बिनियस प्रोटोकॉल की आवश्यकता है। लेकिन पहले, बाइनरी फ़ील्ड पर गहराई से नज़र डालते हैं।

बाइनरी फ़ील्ड्स

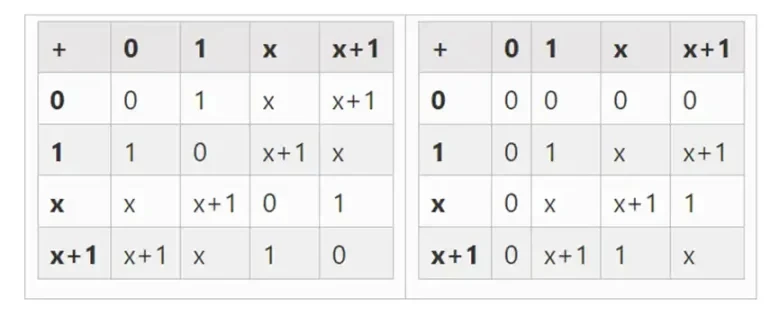
सबसे छोटा सम्भव क्षेत्र अंकगणितीय मॉड्यूलो 2 है, जो इतना छोटा है कि हम इसके लिए जोड़ और गुणन सारणी लिख सकते हैं:

हम विस्तार द्वारा बड़े बाइनरी क्षेत्र प्राप्त कर सकते हैं: यदि हम F 2 (पूर्णांक मॉड्यूलो 2) से शुरू करते हैं और फिर x को परिभाषित करते हैं जहाँ x वर्ग = x + 1, तो हमें निम्नलिखित जोड़ और गुणन सारणी मिलती है:

यह पता चला है कि हम इस निर्माण को दोहराकर बाइनरी फ़ील्ड को मनमाने ढंग से बड़े आकार तक बढ़ा सकते हैं। वास्तविक संख्याओं पर जटिल संख्याओं के विपरीत, जहाँ आप एक नया तत्व जोड़ सकते हैं लेकिन कभी भी कोई और तत्व I नहीं जोड़ सकते (क्वाटर्नियन मौजूद हैं, लेकिन वे गणितीय रूप से अजीब हैं, उदाहरण के लिए ab बराबर ba नहीं है), परिमित फ़ील्ड के साथ आप हमेशा के लिए नए एक्सटेंशन जोड़ सकते हैं। विशेष रूप से, एक तत्व की हमारी परिभाषा इस प्रकार है: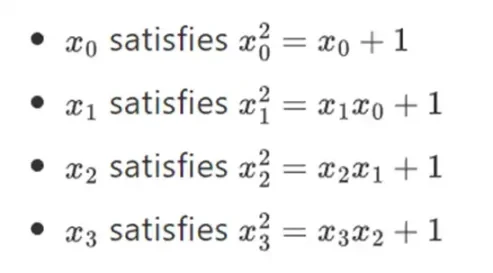

और इसी तरह... इसे अक्सर टावर निर्माण कहा जाता है, क्योंकि प्रत्येक क्रमिक विस्तार को टावर में एक नई परत जोड़ने के रूप में माना जा सकता है। मनमाने आकार के बाइनरी फ़ील्ड बनाने का यह एकमात्र तरीका नहीं है, लेकिन इसके कुछ अनूठे फ़ायदे हैं जिनका बिनियस फ़ायदा उठाता है।

हम इन संख्याओं को बिट्स की सूची के रूप में दर्शा सकते हैं। उदाहरण के लिए, 1100101010001111। पहला बिट 1 के गुणकों को दर्शाता है, दूसरा बिट x0 के गुणकों को दर्शाता है, और फिर निम्नलिखित बिट x1 के गुणकों को दर्शाते हैं: x1, x1*x0, x2, x2*x0, और इसी तरह। यह एन्कोडिंग अच्छी है क्योंकि आप इसे तोड़ सकते हैं:

यह अपेक्षाकृत असामान्य संकेतन है, लेकिन मैं बाइनरी फ़ील्ड तत्वों को पूर्णांक के रूप में प्रस्तुत करना पसंद करता हूँ, जिसमें दाईं ओर अधिक कुशल बिट होता है। यानी, 1 = 1, x0 = 01 = 2, 1+x0 = 11 = 3, 1+x0+x2 = 11001000 = 19, और इसी तरह। इस प्रतिनिधित्व में, यह 61779 है।

बाइनरी फ़ील्ड में जोड़ सिर्फ़ XOR है (और घटाव भी, वैसे); ध्यान दें कि इसका मतलब है कि किसी भी x के लिए x+x = 0 है। दो तत्वों x*y को एक साथ गुणा करने के लिए, एक बहुत ही सरल पुनरावर्ती एल्गोरिथ्म है: प्रत्येक संख्या को आधे में विभाजित करें:

फिर, गुणन को विभाजित करें:

आखिरी हिस्सा ही एकमात्र ऐसा हिस्सा है जो थोड़ा मुश्किल है, क्योंकि आपको सरलीकरण नियम लागू करने होंगे। गुणन करने के लिए और भी अधिक कुशल तरीके हैं, जो करात्सुबा के एल्गोरिदम और फास्ट फूरियर ट्रांसफॉर्म के समान हैं, लेकिन मैं इसे इच्छुक पाठक के लिए एक अभ्यास के रूप में छोड़ दूंगा।

बाइनरी फ़ील्ड में विभाजन गुणन और व्युत्क्रम को मिलाकर किया जाता है। सरल लेकिन धीमी व्युत्क्रम विधि सामान्यीकृत फ़र्मेट्स लिटिल प्रमेय का एक अनुप्रयोग है। एक अधिक जटिल लेकिन अधिक कुशल व्युत्क्रम एल्गोरिथ्म भी है जिसे आप यहाँ पा सकते हैं। बाइनरी फ़ील्ड के जोड़, गुणा और भाग के साथ खेलने के लिए आप यहाँ कोड का उपयोग कर सकते हैं।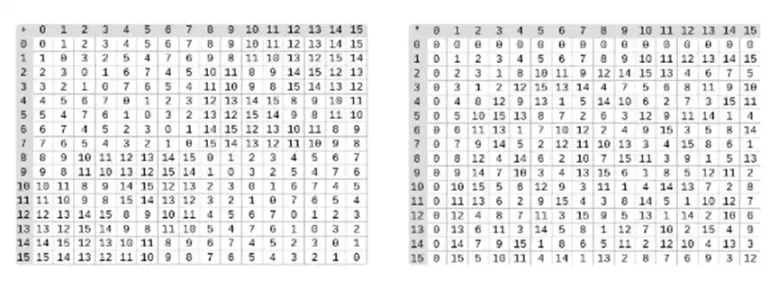

बाएँ: चार-बिट बाइनरी फ़ील्ड तत्वों के लिए योग तालिका (अर्थात, केवल 1, x 0, x 1, x 0x 1)। दाएँ: चार-बिट बाइनरी फ़ील्ड तत्वों के लिए गुणन तालिका।

इस प्रकार के बाइनरी फ़ील्ड की खूबसूरती यह है कि यह नियमित पूर्णांकों और मॉड्यूलर अंकगणित के कुछ बेहतरीन भागों को जोड़ती है। नियमित पूर्णांकों की तरह, बाइनरी फ़ील्ड तत्व असीमित हैं: आप जितना चाहें उतना बड़ा हो सकते हैं। लेकिन मॉड्यूलर अंकगणित की तरह, यदि आप एक निश्चित आकार सीमा के भीतर मूल्यों पर काम करते हैं, तो आपके सभी परिणाम एक ही सीमा में रहेंगे। उदाहरण के लिए, यदि आप 42 को क्रमिक घातों में लेते हैं, तो आपको मिलता है:

255 चरणों के बाद, आप 42 की घात 255 = 1 पर वापस आ जाते हैं, और धनात्मक पूर्णांकों और मॉड्यूलर संक्रियाओं की तरह, वे गणित के सामान्य नियमों का पालन करते हैं: a*b=b*a, a*(b+c)=a*b+a*c, और यहां तक कि कुछ अजीब नए नियम भी।

अंत में, बाइनरी फ़ील्ड बिट्स में हेरफेर करने के लिए सुविधाजनक हैं: यदि आप 2k में फ़िट होने वाली संख्याओं के साथ गणित करते हैं, तो आपका सारा आउटपुट भी 2k बिट्स में फ़िट हो जाएगा। इससे अजीबोगरीब स्थिति से बचा जा सकता है। Ethereum के EIP-4844 में, एक ब्लॉब के अलग-अलग ब्लॉक 52435875175126190479447740508185965837690552500527637822603658699938581184513 के मॉड्यूलो नंबर होने चाहिए, इसलिए बाइनरी डेटा को एन्कोड करने के लिए कुछ जगह छोड़ने और एप्लिकेशन लेयर पर अतिरिक्त जाँच करने की आवश्यकता होती है ताकि यह सुनिश्चित हो सके कि प्रत्येक तत्व में संग्रहीत मान 2248 से कम है। इसका यह भी अर्थ है कि कंप्यूटर पर बाइनरी फ़ील्ड ऑपरेशन बहुत तेज़ हैं - CPU और सैद्धांतिक रूप से इष्टतम FPGA और ASIC डिज़ाइन दोनों।

इसका मतलब यह है कि हम रीड-सोलोमन एनकोडिंग कर सकते हैं जैसा कि हमने ऊपर किया था, एक ऐसे तरीके से जो पूर्णांक विस्फोट से पूरी तरह से बचता है जैसा कि हमने अपने उदाहरण में देखा, और बहुत ही मूल तरीके से, जिस तरह की गणनाएँ कंप्यूटर करने में अच्छे हैं। बाइनरी फ़ील्ड की विभाजित संपत्ति - हम 1100101010001111 = 11001010 + 10001111*x 3 कैसे कर सकते हैं, और फिर इसे अपनी ज़रूरत के अनुसार विभाजित कर सकते हैं - बहुत अधिक लचीलेपन की अनुमति देने के लिए भी महत्वपूर्ण है।

पूर्ण बिनियस

देखना यहाँ प्रोटोकॉल के पायथन कार्यान्वयन के लिए.

अब हम "पूर्ण बिनियस" पर आगे बढ़ सकते हैं, जो "सरल बिनियस" को (i) बाइनरी फ़ील्ड पर काम करने और (ii) हमें एकल बिट्स को प्रतिबद्ध करने के लिए अनुकूलित करता है। इस प्रोटोकॉल को समझना कठिन है क्योंकि यह बिट्स के मैट्रिसेस को देखने के विभिन्न तरीकों के बीच आगे-पीछे स्विच करता है; निश्चित रूप से मुझे इसे समझने में क्रिप्टोग्राफ़िक प्रोटोकॉल को समझने में लगने वाले समय से ज़्यादा समय लगा। लेकिन एक बार जब आप बाइनरी फ़ील्ड को समझ लेते हैं, तो अच्छी खबर यह है कि बिनियस जिस "कठिन गणित" पर निर्भर करता है, वह मौजूद नहीं है। यह एलिप्टिक कर्व पेयरिंग नहीं है, जहाँ नीचे जाने के लिए गहरे और गहरे बीजगणितीय ज्यामिति खरगोश के छेद हैं; यहाँ, आपके पास बस बाइनरी फ़ील्ड हैं।

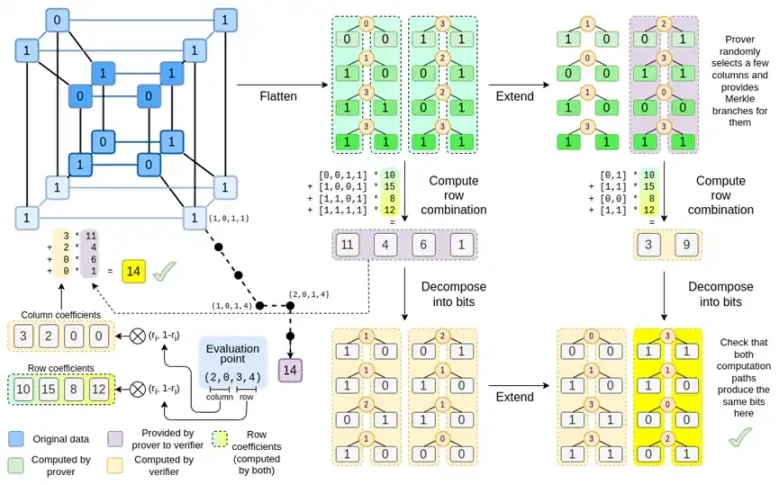
आइये फिर से पूरा चार्ट देखें:

अब तक, आपको अधिकांश घटकों से परिचित होना चाहिए। हाइपरक्यूब को ग्रिड में समतल करने का विचार, मूल्यांकन बिंदुओं के टेंसर उत्पादों के रूप में पंक्ति और स्तंभ संयोजनों की गणना करने का विचार, और रीड-सोलोमन विस्तार के बीच समानता की जाँच करने का विचार फिर पंक्ति संयोजनों की गणना करना और पंक्ति संयोजनों की गणना करना फिर रीड-सोलोमन विस्तार सभी को सादे बिनियस में लागू किया गया है।

कम्पलीट बिनियस में नया क्या है? मूलतः तीन चीजें:

• हाइपरक्यूब और वर्ग में अलग-अलग मान बिट्स (0 या 1) होने चाहिए।

• विस्तार प्रक्रिया बिट्स को स्तंभों में समूहित करके तथा अस्थायी रूप से यह मानकर कि वे एक बड़े क्षेत्र के तत्व हैं, उन्हें अधिक बिट्स में विस्तारित कर देती है।

• पंक्ति संयोजन चरण के बाद, तत्व-वार बिट्स में विघटन चरण होता है जो विस्तार को वापस बिट्स में परिवर्तित कर देता है।

खैर, दोनों मामलों पर बारी-बारी से चर्चा करें। सबसे पहले, नई विस्तार प्रक्रिया। रीड-सोलोमन कोड में एक मौलिक सीमा है, यदि आप n को k*n तक विस्तारित करना चाहते हैं, तो आपको k*n विभिन्न मानों वाले क्षेत्र में काम करने की आवश्यकता है, जिन्हें निर्देशांक के रूप में उपयोग किया जा सकता है। F 2 (उर्फ बिट्स) के साथ, आप ऐसा नहीं कर सकते। इसलिए हम जो करते हैं, वह है, बड़े मान बनाने के लिए F 2 के आसन्न तत्वों को एक साथ पैक करना। यहां उदाहरण में, हम एक बार में दो बिट्स को { 0 , 1 , 2 , 3 } तत्वों में पैक करते हैं, जो हमारे लिए पर्याप्त है क्योंकि हमारे विस्तार में केवल चार गणना बिंदु हैं। वास्तविक प्रमाण में, हम एक बार में 16 बिट्स पीछे जा सकते हैं। फिर हम इन पैक किए गए मूल्यों पर रीड-सोलोमन कोड निष्पादित करते हैं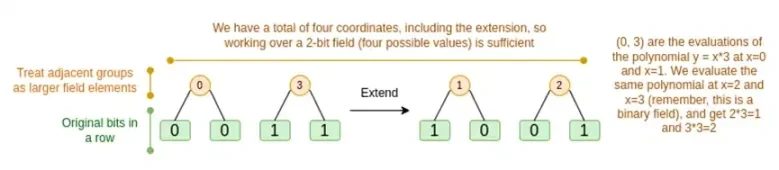

अब, पंक्ति संयोजन। किसी यादृच्छिक बिंदु पर मूल्यांकन को क्रिप्टोग्राफ़िक रूप से सुरक्षित बनाने के लिए, हमें उस बिंदु को काफी बड़े स्थान (हाइपरक्यूब से भी बहुत बड़ा) से नमूना लेने की आवश्यकता है। इसलिए जबकि हाइपरक्यूब के अंदर का बिंदु बिट है, हाइपरक्यूब के बाहर गणना किया गया मान बहुत बड़ा होगा। ऊपर दिए गए उदाहरण में, पंक्ति संयोजन [11, 4, 6, 1] पर समाप्त होता है।

इससे एक समस्या उत्पन्न होती है: हम जानते हैं कि बिट्स को एक बड़े मान में कैसे समूहित किया जाए और फिर उस मान पर रीड-सोलोमन विस्तार कैसे किया जाए, लेकिन हम मानों के बड़े जोड़ों के लिए यही काम कैसे करेंगे?

बिनियस की चाल यह है कि इसे थोड़ा-थोड़ा करके किया जाए: हम प्रत्येक मान के एक बिट को देखते हैं (उदाहरण के लिए, जिस चीज़ को हमने 11 लेबल किया है, वह [1, 1, 0, 1] है), और फिर हम इसे पंक्ति दर पंक्ति विस्तारित करते हैं। यानी, हम इसे प्रत्येक तत्व की 1 पंक्ति पर विस्तारित करते हैं, फिर x0 पंक्ति पर, फिर x1 पंक्ति पर, फिर x0x1 पंक्ति पर, और इसी तरह आगे बढ़ते हैं (खैर, हमारे खिलौने के उदाहरण में हम यहीं रुक जाते हैं, लेकिन वास्तविक कार्यान्वयन में हम 128 पंक्तियों तक जाएंगे (अंतिम पंक्ति x6*…*x0 है))

समीक्षा:

• हम हाइपरक्यूब में बिट्स को ग्रिड में परिवर्तित करते हैं

• फिर हम प्रत्येक पंक्ति पर आसन्न बिट्स के समूहों को एक बड़े क्षेत्र के तत्वों के रूप में मानते हैं और पंक्ति को रीड-सोलोमन तरीके से विस्तारित करने के लिए उन पर अंकगणितीय ऑपरेशन करते हैं

• फिर हम बिट्स के प्रत्येक कॉलम का पंक्ति संयोजन लेते हैं और प्रत्येक पंक्ति के लिए बिट्स का कॉलम आउटपुट के रूप में प्राप्त करते हैं (4 x 4 से बड़े वर्गों के लिए बहुत छोटा)

• फिर, हम आउटपुट को मैट्रिक्स और उसके बिट्स को पंक्तियों के रूप में मानते हैं

ऐसा क्यों हो रहा है? सामान्य गणित में, यदि आप किसी संख्या को बिट-बाय-बिट स्लाइस करना शुरू करते हैं, तो किसी भी क्रम में रैखिक संचालन करने और समान परिणाम प्राप्त करने की (सामान्य) क्षमता टूट जाती है। उदाहरण के लिए, यदि मैं संख्या 345 से शुरू करता हूं, और इसे 8 से गुणा करता हूं, फिर 3 से, तो मुझे 8280 मिलता है, और यदि मैं उन दो ऑपरेशनों को उलट देता हूं, तो मुझे भी 8280 मिलता है। लेकिन अगर मैं दो चरणों के बीच एक बिट-स्लाइसिंग ऑपरेशन डालता हूं, तो यह टूट जाता है: यदि आप 8x करते हैं, फिर 3x करते हैं, तो आपको मिलता है: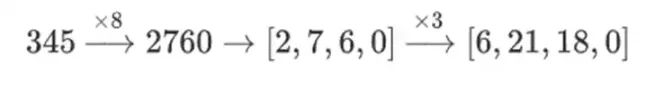

लेकिन यदि आप 3x, फिर 8x करते हैं, तो आपको मिलता है:

लेकिन टावर संरचनाओं के साथ निर्मित बाइनरी फ़ील्ड में, यह दृष्टिकोण काम करता है। इसका कारण उनकी पृथक्करणीयता है: यदि आप किसी बड़े मान को किसी छोटे मान से गुणा करते हैं, तो प्रत्येक खंड पर जो होता है वह प्रत्येक खंड पर रहता है। यदि हम 1100101010001111 को 11 से गुणा करते हैं, तो यह 1100101010001111 के पहले अपघटन के समान है, जो है

फिर प्रत्येक घटक को 11 से गुणा करें।

यह सब एक साथ डालें

सामान्य तौर पर, शून्य-ज्ञान प्रमाण प्रणाली एक बहुपद के बारे में कथन बनाकर काम करती है जो एक ही समय में अंतर्निहित मूल्यांकन के बारे में कथनों का प्रतिनिधित्व करती है: जैसा कि हमने फिबोनाची उदाहरण में देखा, F(X+ 2)-F(X+ 1)-F(X) = Z(X)*H(X) फिबोनाची गणना के सभी चरणों की जाँच करते समय। हम यादृच्छिक बिंदुओं पर मूल्यांकन साबित करके बहुपद के बारे में कथनों की जाँच करते हैं। यादृच्छिक बिंदुओं की यह जाँच पूरे बहुपद की जाँच का प्रतिनिधित्व करती है: यदि बहुपद समीकरण मेल नहीं खाता है, तो एक छोटी सी संभावना है कि यह एक विशिष्ट यादृच्छिक निर्देशांक पर मेल खाता है।

व्यवहार में, अक्षमता का एक प्रमुख स्रोत यह है कि वास्तविक कार्यक्रमों में, हम जिन संख्याओं से निपटते हैं, उनमें से अधिकांश छोटी होती हैं: फॉर लूप्स में इंडेक्स, ट्रू/फाल्स मान, काउंटर और ऐसी ही अन्य चीजें। हालाँकि, जब हम मर्कल-प्रूफ-आधारित जाँच को सुरक्षित बनाने के लिए आवश्यक अतिरेक प्रदान करने के लिए रीड-सोलोमन एन्कोडिंग के साथ डेटा का विस्तार करते हैं, तो अधिकांश अतिरिक्त मान फ़ील्ड के पूरे आकार को ले लेते हैं, भले ही मूल मान छोटा हो।

इसे ठीक करने के लिए, हम इस फ़ील्ड को यथासंभव छोटा बनाना चाहते हैं। प्लॉन्की 2 ने हमें 256-बिट संख्याओं से 64-बिट संख्याओं तक पहुँचाया, और फिर प्लॉन्की 3 ने इसे और कम करके 31 बिट कर दिया। लेकिन यह भी इष्टतम नहीं है। बाइनरी फ़ील्ड के साथ, हम सिंगल बिट्स से निपट सकते हैं। यह एन्कोडिंग को सघन बनाता है: यदि आपके वास्तविक अंतर्निहित डेटा में n बिट्स हैं, तो आपके एन्कोडिंग में n बिट्स होंगे, और विस्तार में 8*n बिट्स होंगे, बिना किसी अतिरिक्त ओवरहेड के।

अब, आइए इस चार्ट को तीसरी बार देखें:

बिनियस में, हम एक बहुरेखीय बहुपद पर काम करते हैं: एक हाइपरक्यूब P(x0, x1,…xk) जहाँ एकल मूल्यांकन P(0, 0, 0, 0), P(0, 0, 0, 1) से लेकर P(1, 1, 1, 1) तक, वह डेटा रखते हैं जिसकी हमें परवाह है। किसी निश्चित बिंदु पर गणना को साबित करने के लिए, हम उसी डेटा को एक वर्ग के रूप में फिर से व्याख्या करते हैं। फिर हम प्रत्येक पंक्ति का विस्तार करते हैं, रीड-सोलोमन एन्कोडिंग का उपयोग करके यादृच्छिक मर्कल शाखा प्रश्नों के विरुद्ध सुरक्षा के लिए आवश्यक डेटा अतिरेक प्रदान करते हैं। फिर हम पंक्तियों के यादृच्छिक रैखिक संयोजनों की गणना करते हैं, गुणांकों को डिज़ाइन करते हैं ताकि नई संयुक्त पंक्ति में वास्तव में वह गणना मूल्य शामिल हो जिसकी हमें परवाह है। यह नई बनाई गई पंक्ति (128-बिट पंक्ति के रूप में पुनर्व्याख्या की गई) और मर्कल शाखाओं के साथ कुछ यादृच्छिक रूप से चयनित कॉलम सत्यापनकर्ता को दिए जाते हैं।

सत्यापनकर्ता फिर विस्तारित पंक्ति संयोजन (या अधिक सटीक रूप से, विस्तारित कॉलम) और विस्तारित पंक्ति संयोजन करता है और सत्यापित करता है कि दोनों मेल खाते हैं। फिर यह एक कॉलम संयोजन की गणना करता है और जाँचता है कि यह प्रूवर द्वारा दावा किए गए मान को लौटाता है। यह हमारा प्रमाण प्रणाली है (या अधिक सटीक रूप से, बहुपद प्रतिबद्धता योजना, जो प्रमाण प्रणाली का एक प्रमुख घटक है)।

हमने अभी तक क्या कवर नहीं किया है?

• पंक्तियों का विस्तार करने के लिए एक कुशल एल्गोरिथ्म की आवश्यकता होती है ताकि सत्यापनकर्ता को वास्तव में कम्प्यूटेशनल रूप से कुशल बनाया जा सके। हम बाइनरी फ़ील्ड पर फास्ट फूरियर ट्रांसफ़ॉर्म का उपयोग करते हैं, जिसका वर्णन यहाँ किया गया है (हालाँकि सटीक कार्यान्वयन अलग होगा, क्योंकि यह पोस्ट एक कम कुशल निर्माण का उपयोग करता है जो पुनरावर्ती विस्तार पर आधारित नहीं है)।

• अंकगणितीय रूप से। एकचर बहुपद सुविधाजनक होते हैं क्योंकि आप गणना में आसन्न चरणों को जोड़ने के लिए F(X+2)-F(X+1)-F(X) = Z(X)*H(X) जैसी चीजें कर सकते हैं। हाइपरक्यूब में, अगला चरण X+1 की तुलना में बहुत कम अच्छी तरह से समझाया गया है। आप X+k, k की घातें कर सकते हैं, लेकिन यह जंपिंग व्यवहार बिनियस के कई प्रमुख लाभों का त्याग करता है। बिनियस पेपर समाधान का वर्णन करता है। अनुभाग 4.3 देखें), लेकिन यह अपने आप में एक गहरा खरगोश का छेद है।

• विशिष्ट मान जाँच को सुरक्षित तरीके से कैसे करें। फिबोनाची उदाहरण में मुख्य सीमा स्थितियों की जाँच की आवश्यकता थी: F(0)=F(1)=1 और F(100) के मान। लेकिन मूल बिनियस के लिए, ज्ञात गणना बिंदुओं पर जाँच करना असुरक्षित है। तथाकथित योग-जाँच प्रोटोकॉल का उपयोग करके ज्ञात गणना जाँच को अज्ञात गणना जाँच में बदलने के कुछ काफी सरल तरीके हैं; लेकिन हम यहाँ उन पर चर्चा नहीं करेंगे।

• लुकअप प्रोटोकॉल, एक और तकनीक जिसका हाल ही में व्यापक रूप से उपयोग किया गया है, का उपयोग सुपर कुशल प्रूफ सिस्टम बनाने के लिए किया जाता है। बिनियस का उपयोग कई अनुप्रयोगों के लिए लुकअप प्रोटोकॉल के साथ किया जा सकता है।

• वर्गमूल सत्यापन समय से परे। वर्गमूल महंगे हैं: 2^32 बिट्स का एक बिनियस प्रूफ लगभग 11 एमबी लंबा है। आप बिनियस प्रूफ के प्रूफ बनाने के लिए अन्य प्रूफ सिस्टम का उपयोग करके इसकी भरपाई कर सकते हैं, जिससे आपको छोटे प्रूफ साइज वाले बिनियस प्रूफ की दक्षता मिलती है। एक अन्य विकल्प अधिक जटिल FRI-Binius प्रोटोकॉल है, जो मल्टी-लॉगरिदमिक साइज (नियमित FRI की तरह) का प्रूफ बनाता है।

• बिनियस SNARK-मित्रता को कैसे प्रभावित करता है। मूल सारांश यह है कि यदि आप बिनियस का उपयोग करते हैं, तो आपको अब गणनाओं को अंकगणित-अनुकूल बनाने के बारे में चिंता करने की आवश्यकता नहीं है: नियमित हैशिंग अब पारंपरिक अंकगणितीय हैशिंग से अधिक कुशल नहीं है, 32 की घात के लिए 2 के मॉड्यूलो का गुणन या 256 की घात के लिए 2 के मॉड्यूलो का गुणन अब 2 के मॉड्यूलो के गुणन जितना दर्दनाक नहीं है, आदि। लेकिन यह एक जटिल विषय है। जब सब कुछ बाइनरी में किया जाता है तो बहुत सी चीजें बदल जाती हैं।

मुझे आने वाले महीनों में बाइनरी फील्ड आधारित प्रूफ प्रौद्योगिकी में और अधिक सुधार देखने की उम्मीद है।

यह लेख इंटरनेट से लिया गया है: विटालिक: बिनियस, बाइनरी क्षेत्रों के लिए कुशल प्रमाण

संबंधित: बीएनबी कॉइन में सुधार के संकेत: नया वार्षिक उच्च स्तर दिखाई दे रहा है

संक्षेप में BNB की कीमत $550 से वापस उछलकर $593 प्रतिरोध को तोड़ने के करीब पहुंच गई है। मूल्य संकेतकों ने तेजी की गति को पुनः प्राप्त कर लिया है, जो 8% की वृद्धि का समर्थन करता है। 4.03 पर शार्प अनुपात संभवतः नए निवेशकों को एक्सचेंज टोकन की ओर आकर्षित करेगा। मार्च BNB कॉइन के लिए एक अनुकूल महीना था, जिसमें क्रिप्टोकरेंसी ने सुधार का अनुभव करने से पहले कुछ ही दिनों में वर्ष के लिए दो नए उच्च स्तर प्राप्त किए। लगभग दो सप्ताह की रिकवरी अवधि के बाद, BNB कॉइन 2024 में संभावित रूप से एक नए उच्च स्तर पर पहुंचने के संकेत दे रहा है। लेकिन क्या ऐसा मील का पत्थर हासिल किया जा सकता है? BNB आशाजनक लग रहा है $550 समर्थन स्तर से पलटाव के बाद, इस विश्लेषण के समय BNB कॉइन का मूल्य $581 तक बढ़ गया है। यह सुधार altcoin के जोखिम-वापसी प्रोफ़ाइल में सुधार को दर्शाता है,…