Vitalik: Binius, pruebas eficientes para campos binarios

Artículo original de: Vitalik Buterin

Traducción original: Kate, MarsBit

Esta publicación está dirigida principalmente a lectores que generalmente están familiarizados con la criptografía de la era 2019, y con los SNARK y STARK en particular. Si no es así, recomiendo leerlos primero. Un agradecimiento especial a Justin Drake, Jim Posen, Benjamin Diamond y Radi Cojbasic por sus comentarios y opiniones.

En los últimos dos años, los STARK se han convertido en una tecnología clave e irremplazable para realizar de manera eficiente pruebas criptográficas fácilmente verificables de declaraciones muy complejas (por ejemplo, probar que un bloque de Ethereum es válido). Una de las razones clave para esto es el pequeño tamaño de campo: los SNARK basados en curvas elípticas requieren que trabajes con números enteros de 256 bits para ser lo suficientemente seguros, mientras que los STARK te permiten usar tamaños de campo mucho más pequeños con mayor eficiencia: primero el campo Goldilocks (número entero de 64 bits), luego Mersenne 31 y BabyBear (ambos de 31 bits). Debido a estas ganancias de eficiencia, Plonky 2 que usa Goldilocks es cientos de veces más rápido que sus predecesores a la hora de probar muchos tipos de cálculos.

Una pregunta natural es: ¿podemos llevar esta tendencia a su conclusión lógica y construir sistemas de prueba que funcionen más rápido operando directamente con ceros y unos? Esto es exactamente lo que intenta hacer Binius, utilizando una serie de trucos matemáticos que lo hacen muy diferente de los SNARK y STARK de hace tres años. Esta publicación describe por qué los campos pequeños hacen que la generación de pruebas sea más eficiente, por qué los campos binarios son excepcionalmente poderosos y los trucos que utiliza Binius para hacer que las pruebas en campos binarios sean tan eficientes.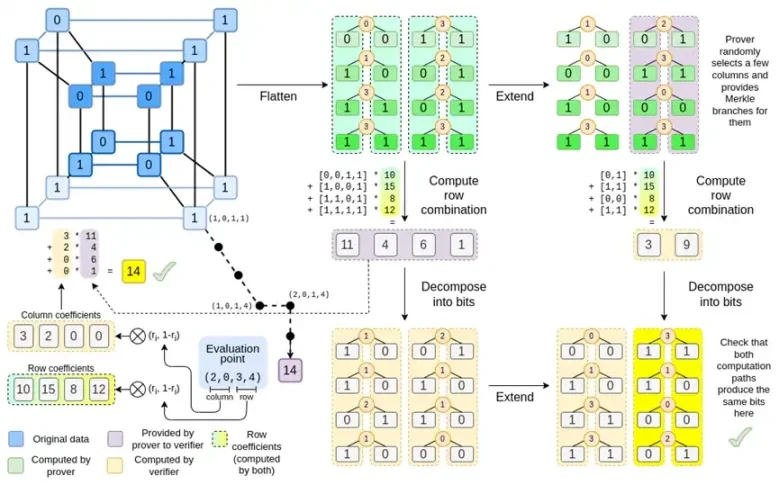

Binius, al final de esta publicación, deberías poder comprender cada parte de este diagrama.

Revisión: campos finitos

Una de las tareas clave de los sistemas de prueba criptográfica es operar con grandes cantidades de datos manteniendo los números pequeños. Si puede comprimir una afirmación sobre un programa grande en una ecuación matemática que contenga unos pocos números, pero esos números son tan grandes como el programa original, entonces no habrá ganado nada.

Para realizar aritmética compleja manteniendo números pequeños, los criptógrafos suelen utilizar aritmética modular. Elegimos un módulo de número primo p. El operador % significa tomar el resto: 15% 7 = 1, 53% 10 = 3, y así sucesivamente. (Tenga en cuenta que la respuesta siempre es no negativa, por ejemplo -1% 10 = 9)

Es posible que hayas visto la aritmética modular en el contexto de sumar y restar tiempo (por ejemplo, ¿qué hora son 4 horas después de las 9?). Pero aquí, no sólo sumamos y restamos módulo de un número; también podemos multiplicar, dividir y tomar exponentes.

Redefinimos:

Las reglas anteriores son todas autoconsistentes. Por ejemplo, si p = 7, entonces:

5 + 3 = 1 (porque 8% 7 = 1)

1-3 = 5 (porque -2% 7 = 5)

2* 5 = 3

3/5 = 2

Un término más general para este tipo de estructuras es campos finitos. Un campo finito es una estructura matemática que sigue las leyes habituales de la aritmética, pero en la que el número de valores posibles es finito, de modo que cada valor puede representarse mediante un tamaño fijo.

La aritmética modular (o campos primos) es el tipo más común de campo finito, pero existe otro tipo: los campos de extensión. Es posible que hayas visto un campo de extensión: los números complejos. Imaginamos un nuevo elemento y lo etiquetamos i, y hacemos cálculos con él: (3i+2)*(2i+4)=6i*i+12i+4i+8=16i+2. Podemos hacer lo mismo con la extensión del campo primo. A medida que comenzamos a trabajar con campos más pequeños, la extensión de los campos primos se vuelve cada vez más importante para la seguridad, y los campos binarios (utilizados por Binius) dependen completamente de la extensión para tener utilidad práctica.

Revisión: aritmetización

La forma en que los SNARK y STARK prueban programas de computadora es a través de la aritmética: se toma una afirmación sobre el programa que se desea probar y se la convierte en una ecuación matemática que involucra un polinomio. Una solución válida de la ecuación corresponde a una ejecución válida del programa.

Como ejemplo simple, supongamos que calculé el número 100 de Fibonacci y quiero demostrarles cuál es. Creo un polinomio F que codifica la secuencia de Fibonacci: entonces F(0)=F(1)=1, F(2)=2, F(3)=3, F(4)=5 y así sucesivamente durante 100 pasos . La condición que necesito demostrar es que F(x+2)=F(x)+F(x+1) en todo el rango x={0, 1…98}. Puedo convencerte dándote el cociente:

donde Z(x) = (x-0) * (x-1) * …(x-98). . Si puedo proporcionar que F y H satisfagan esta ecuación, entonces F debe satisfacer F(x+ 2)-F(x+ 1)-F(x) en el rango. Si además verifico que para F, F(0)=F(1)=1, entonces F(100) debe ser en realidad el número 100 de Fibonacci.

Si quieres demostrar algo más complicado, entonces reemplazas la relación simple F(x+2) = F(x) + F(x+1) con una ecuación más complicada que básicamente dice que F(x+1) es la salida. de inicializar una máquina virtual con el estado F(x) y ejecutar un paso computacional. También puede reemplazar el número 100 con un número mayor, por ejemplo, 100000000, para dar cabida a más pasos.

Todos los SNARK y STARK se basan en la idea de utilizar ecuaciones simples sobre polinomios (y, a veces, vectores y matrices) para representar un gran número de relaciones entre valores individuales. No todos los algoritmos verifican la equivalencia entre pasos computacionales adyacentes como el anterior: por ejemplo, PLONK no lo hace y R1CS tampoco. Pero muchas de las comprobaciones más eficaces lo hacen porque es más fácil minimizar los gastos generales realizando la misma comprobación (o las mismas pocas comprobaciones) muchas veces.

Plonky 2: De SNARK y STARK de 256 bits a 64 bits… solo STARK

Hace cinco años, un resumen razonable de los diferentes tipos de pruebas de conocimiento cero era el siguiente. Hay dos tipos de pruebas: SNARK (basadas en curvas elípticas) y STARK (basadas en hash). Técnicamente, los STARK son un tipo de SNARK, pero en la práctica, es común usar "SNARK" para referirse a la variante basada en curva elíptica y "STARK" para referirse a la construcción basada en hash. Los SNARK son pequeños, por lo que puedes verificarlos muy rápidamente e instalarlos en la cadena fácilmente. Los STARK son grandes, pero no requieren una configuración confiable y son resistentes a los cuánticos.

Los STARK funcionan tratando los datos como un polinomio, calculando el cálculo de ese polinomio y utilizando la raíz de Merkle de los datos extendidos como un "compromiso polinómico".

Una pieza clave de la historia aquí es que los SNARK basados en curvas elípticas se usaron ampliamente primero: los STARK no se volvieron lo suficientemente eficientes hasta alrededor de 2018, gracias a FRI, y para entonces Zcash había estado funcionando durante más de un año. Los SNARK basados en curvas elípticas tienen una limitación clave: si desea utilizar un SNARK basado en curvas elípticas, entonces la aritmética en estas ecuaciones debe realizarse en módulo del número de puntos en la curva elíptica. Este es un número grande, generalmente cercano a 2 elevado a 256: por ejemplo, para la curva bn128 es 21888242871839275222246405745257275088548364400416034343698204186575808495617. Pero la computación real usa números pequeños: si piensas sobre un programa real en tu idioma favorito, la mayoría de las cosas Los usos son contadores, índices en bucles for, posiciones en el programa, bits individuales que representan Verdadero o Falso y otras cosas que casi siempre tienen solo unos pocos dígitos.

Incluso si sus datos originales consisten en números pequeños, el proceso de prueba requiere calcular cocientes, expansiones, combinaciones lineales aleatorias y otras transformaciones de datos que darán como resultado un número igual o mayor de objetos que en promedio son tan grandes como el tamaño completo de su campo. Esto crea una ineficiencia clave: para probar un cálculo con n valores pequeños, hay que hacer muchos más cálculos con n valores mucho más grandes. Inicialmente, los STARK heredaron el hábito SNARK de utilizar campos de 256 bits y, por lo tanto, padecían la misma ineficiencia.

Expansión de Reed-Solomon de alguna evaluación polinómica. Aunque el valor original es pequeño, los valores adicionales se expanden al tamaño completo del campo (en este caso 2^31 – 1)

En 2022, se lanzó Plonky 2. La principal innovación de Plonky 2 es hacer aritmética módulo de un número primo más pequeño: 2 elevado a 64 – 2 elevado a 32 + 1 = 18446744067414584321. Ahora, cada suma o multiplicación siempre se puede hacer con unas pocas instrucciones en el CPU y combinar todos los datos es 4 veces más rápido que antes. Pero hay un problema: este método sólo funciona para STARK. Si intenta utilizar SNARK, las curvas elípticas se vuelven inseguras para curvas elípticas tan pequeñas.

Para garantizar la seguridad, Plonky 2 también necesita introducir campos de extensión. Una técnica clave para verificar ecuaciones aritméticas es el muestreo puntual aleatorio: si desea verificar si H(x) * Z(x) es igual a F(x+ 2)-F(x+ 1)-F(x), puede hacerlo aleatoriamente. elija una coordenada r, proporcione un compromiso polinómico para demostrar H(r), Z(r), F(r), F(r+ 1) y F(r+ 2), y luego verifique si H(r) * Z(r ) es igual a F(r+ 2)-F(r+ 1)- F(r). Si un atacante puede adivinar las coordenadas de antemano, entonces puede engañar al sistema de prueba; por eso el sistema de prueba debe ser aleatorio. Pero esto también significa que las coordenadas deben tomarse de un conjunto lo suficientemente grande como para que el atacante no pueda adivinar al azar. Obviamente, esto es cierto si el módulo está cerca de 2 elevado a 256. Sin embargo, para el módulo 2^64 – 2^32 + 1, aún no hemos llegado a ese punto, y este ciertamente no es el caso si bajamos a 2^31 – 1. Está dentro de las capacidades de un atacante intentar falsificar una prueba dos mil millones de veces hasta que tenga suerte.

Para evitar esto, tomamos una muestra de r de un campo extendido, de modo que, por ejemplo, pueda definir y donde y^3 = 5 y tomar combinaciones de 1, y e y^2. Esto eleva el número total de coordenadas a aproximadamente 2^93. La mayoría de los polinomios calculados por el probador no entran en este campo extendido; son solo números enteros módulo 2^31-1, por lo que aún obtienes toda la eficiencia al usar un campo pequeño. Pero las verificaciones aleatorias de puntos y los cálculos de FRI llegan a este campo más amplio para obtener la seguridad que necesitan.

De los pequeños números primos a los números binarios

Las computadoras hacen aritmética representando números más grandes como secuencias de 0 y 1, y construyendo circuitos sobre esos bits para calcular operaciones como la suma y la multiplicación. Las computadoras están particularmente optimizadas para números enteros de 16, 32 y 64 bits. Por ejemplo, 2^64 – 2^32 + 1 y 2^31 – 1 se eligieron no solo porque encajan dentro de esos límites, sino también porque encajan bien dentro de esos límites: módulo de multiplicación 2^64 – 2^32 + 1 se puede realizar haciendo una multiplicación regular de 32 bits y desplazando y copiando bit a bit la salida en algunos lugares; Este artículo explica muy bien algunos de los trucos.

Sin embargo, un enfoque mucho mejor sería realizar los cálculos directamente en binario. ¿Qué pasaría si la suma pudiera ser simplemente XOR, sin tener que preocuparse por el arrastre de sumar 1 + 1 de un bit al siguiente? ¿Qué pasaría si la multiplicación pudiera paralelizarse más de la misma manera? Todas estas ventajas se basan en la capacidad de representar valores verdadero/falso con un solo bit.

Obtener estas ventajas de realizar cálculos binarios directamente es exactamente lo que Binius está tratando de hacer. El equipo de Binius demostró las ganancias en eficiencia en su presentación en zkSummit:

A pesar de tener aproximadamente el mismo tamaño, las operaciones en campos binarios de 32 bits requieren 5 veces menos recursos computacionales que las operaciones en campos Mersenne de 31 bits.

De polinomios univariados a hipercubos

Supongamos que creemos en este razonamiento y queremos hacer todo con los bits (0 y 1). ¿Cómo podemos representar mil millones de bits con un solo polinomio?

Aquí nos enfrentamos a dos problemas prácticos:

1. Para que un polinomio represente una gran cantidad de valores, estos valores deben ser accesibles al evaluar el polinomio: en el ejemplo de Fibonacci anterior, F(0), F(1) … F(100), y en un cálculo más amplio , los exponentes serán de millones. Los campos que utilizamos deben contener números de este tamaño.

2. Probar cualquier valor que cometamos en un árbol Merkle (como todos los STARK) requiere que Reed-Solomon lo codifique: por ejemplo, expandir los valores de n a 8n, usar redundancia para evitar que probadores maliciosos hagan trampa falsificando un valor durante el cálculo. Esto también requiere tener un campo lo suficientemente grande: para expandir desde un millón de valores a 8 millones, necesitas 8 millones de puntos diferentes para evaluar el polinomio.

Una idea clave de Binius es resolver estos dos problemas por separado, y hacerlo representando los mismos datos de dos formas diferentes. Primero, los polinomios mismos. Los sistemas como los SNARK basados en curvas elípticas, los STARK de la era 2019, Plonky 2 y otros suelen trabajar con polinomios sobre una variable: F(x). Binius, por otro lado, se inspira en el protocolo Spartan y utiliza polinomios multivariados: F(x 1, x 2,… xk). De hecho, representamos toda la trayectoria computacional en un hipercubo de cálculo, donde cada xi es 0 o 1. Por ejemplo, si queremos representar una secuencia de Fibonacci y aún usamos un campo lo suficientemente grande para representarlas, podemos Imagina sus primeras 16 secuencias así: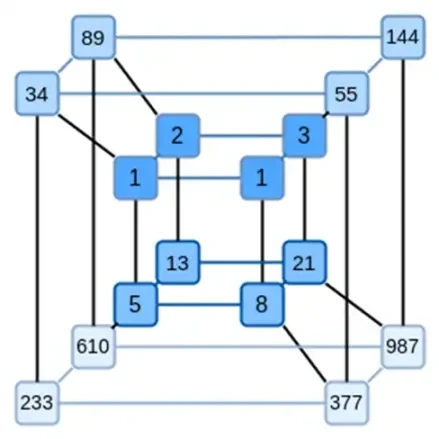

Es decir, F(0,0,0,0) debe ser 1, F(1,0,0,0) también es 1, F(0,1,0,0) es 2, y así sucesivamente, todos los hasta F(1,1,1,1) = 987. Dado tal hipercubo de cálculos, existe un polinomio lineal multivariado (grado 1 en cada variable) que produce estos cálculos. Entonces podemos pensar que este conjunto de valores representa el polinomio; No necesitamos calcular los coeficientes.

Por supuesto, este ejemplo es sólo para ilustrar: en la práctica, el objetivo de entrar en el hipercubo es permitirnos tratar con bits individuales. La forma nativa de Binius de calcular los números de Fibonacci es utilizar un cubo de dimensiones superiores, almacenando un número por grupo de, digamos, 16 bits. Esto requiere cierta astucia para implementar la suma de enteros en bits, pero para Binius, no es demasiado difícil.

Ahora, veamos los códigos de borrado. La forma en que funcionan los STARK es que tomas n valores, Reed-Solomon los expande a más valores (generalmente 8n, generalmente entre 2n y 32n), luego seleccionas aleatoriamente algunas ramas de Merkle de la expansión y realizas algún tipo de verificación sobre ellas. El hipercubo tiene una longitud de 2 en cada dimensión. Por lo tanto, no es práctico expandirlo directamente: no hay suficiente espacio para muestrear ramas de Merkle a partir de 16 valores. Entonces, ¿Cómo lo hacemos? ¡Supongamos que el hipercubo es un cuadrado!

Binius simple: un ejemplo

Ver aquí para una implementación del protocolo en Python.

Veamos un ejemplo, usando números enteros regulares como nuestros campos por conveniencia (en una implementación real, usaríamos elementos de campo binarios). Primero, codificamos el hipercubo que queremos enviar como un cuadrado:

Ahora, ampliamos el cuadrado usando el método de Reed-Solomon. Es decir, tratamos cada fila como un polinomio de grado 3 evaluado en x = { 0, 1, 2, 3 } y evaluamos el mismo polinomio en x = { 4, 5, 6, 7 }: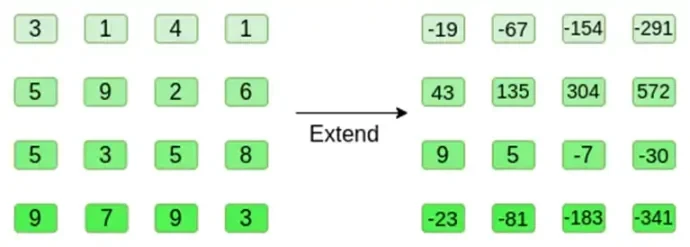

¡Tenga en cuenta que los números pueden volverse realmente grandes! Es por eso que en implementaciones prácticas siempre usamos campos finitos, en lugar de números enteros regulares: si usamos números enteros módulo 11, por ejemplo, la expansión de la primera fila será simplemente [3, 10, 0, 6].

Si desea probar la extensión y verificar los números usted mismo, puede usar mi código de extensión simple Reed-Solomon aquí.

A continuación, tratamos esta extensión como una columna y creamos un árbol Merkle de la columna. La raíz del árbol Merkle es nuestro compromiso.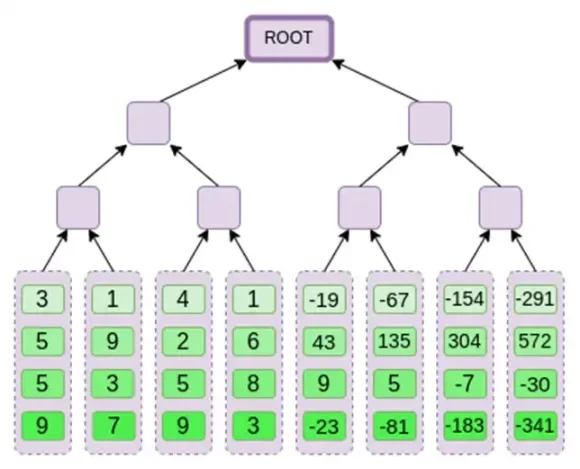

Ahora, supongamos que el probador quiere probar el cálculo de este polinomio r = {r 0, r 1, r 2, r 3 } en algún momento. Hay una sutil diferencia en Binius que lo hace más débil que otros esquemas de compromiso polinómico: el probador no debe saber ni ser capaz de adivinar s antes de comprometerse con la raíz de Merkle (en otras palabras, r debe ser un valor pseudoaleatorio que depende de la raíz de Merkle). Esto hace que el esquema sea inútil para búsquedas en bases de datos (por ejemplo, ok, me diste la raíz de Merkle, ¡ahora demuéstrame P(0, 0, 1, 0)!). Pero los protocolos de prueba de conocimiento cero que utilizamos normalmente no requieren búsquedas en bases de datos; sólo requieren verificar el polinomio en un punto de evaluación aleatorio. Entonces esta restricción sirve bien a nuestros propósitos.

Supongamos que elegimos r = {1, 2, 3, 4} (el polinomio se evalúa como -137; puede confirmarlo usando este código). Ahora llegamos a la prueba. Dividimos r en dos partes: la primera parte {1, 2} representa la combinación lineal de las columnas dentro de la fila, y la segunda parte {3, 4} representa la combinación lineal de las filas. Calculamos un producto tensorial y para las columnas:

Para la parte de la fila:

Esto significa: una lista de todos los productos posibles de un valor en cada conjunto. En el caso de la fila, obtenemos:

[( 1-r 2)*( 1-r 3), ( 1-r 3), ( 1-r 2)*r 3, r 2*r 3 ]

Con r = { 1, 2, 3, 4 } (entonces r 2 = 3 y r 3 = 4):

[( 1-3)*( 1-4), 3*( 1-4),( 1-3)* 4, 3* 4 ] = [ 6, -9 -8 -12 ]

Ahora calculamos una nueva fila t tomando una combinación lineal de las filas existentes. Es decir, tomamos:

Puedes pensar en lo que está sucediendo aquí como una evaluación parcial. Si multiplicamos el producto tensor completo por el vector completo de todos los valores, obtendrías el cálculo P(1, 2, 3, 4) = -137. Aquí, multiplicamos el producto tensorial parcial usando solo la mitad de las coordenadas de evaluación y reducimos la cuadrícula de N valores a una sola fila de N valores de raíz cuadrada. Si le da esta fila a otra persona, podrá hacer el resto del cálculo utilizando el producto tensorial de la otra mitad de las coordenadas de evaluación.

El probador proporciona al verificador la siguiente fila nueva: t y una prueba de Merkle de algunas columnas muestreadas aleatoriamente. En nuestro ejemplo ilustrativo, haremos que el probador proporcione solo la última columna; en la vida real, el probador necesitaría proporcionar docenas de columnas para lograr la seguridad adecuada.

Ahora explotamos la linealidad de los códigos Reed-Solomon. La propiedad clave que explotamos es que tomar una combinación lineal de expansiones de Reed-Solomon da el mismo resultado que tomar una expansión de Reed-Solomon de una combinación lineal. Esta independencia secuencial suele ocurrir cuando ambas operaciones son lineales.

El verificador hace exactamente eso. Calculan t, y calculan combinaciones lineales de las mismas columnas que el probador calculó antes (pero solo las columnas proporcionadas por el probador), y verifican que los dos procedimientos den la misma respuesta.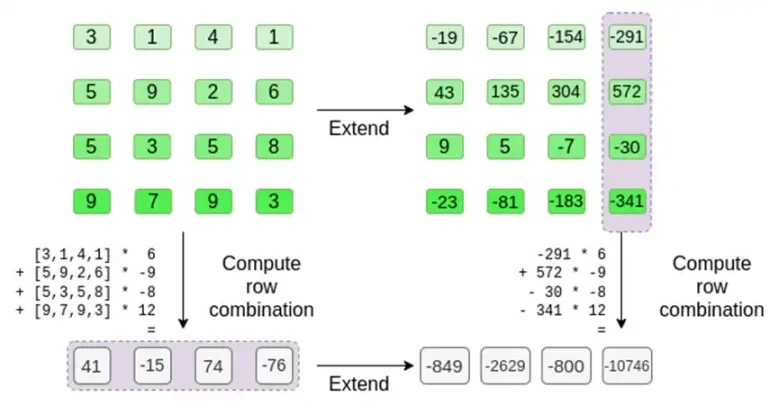

En este caso, expandimos t y calculamos la misma combinación lineal ([6,-9,-8, 12]), y ambas dan la misma respuesta: -10746. Esto prueba que la raíz de Merkle se construyó de buena fe (o al menos lo suficientemente cerca) y que coincide con t: al menos la gran mayoría de las columnas son compatibles entre sí.

Pero hay una cosa más que el verificador debe verificar: verificar la evaluación del polinomio {r 0 …r 3 }. Todos los pasos del verificador hasta ahora no han dependido realmente del valor declarado por el probador. Así es como lo comprobamos. Tomamos el producto tensorial de la “parte de la columna” que marcamos como punto de cálculo: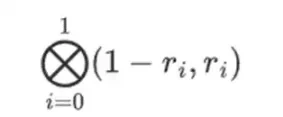

En nuestro caso, donde r = { 1, 2, 3, 4 } por lo que la mitad de las columnas seleccionadas es { 1, 2 }), esto equivale a:

Ahora tomamos esta combinación lineal t:

Esto es lo mismo que resolver directamente el polinomio.

Lo anterior se acerca mucho a una descripción completa del protocolo simple de Binius. Esto ya tiene algunas ventajas interesantes: por ejemplo, como los datos están separados en filas y columnas, sólo necesitas un campo de la mitad del tamaño. Sin embargo, esto no logra todos los beneficios de la computación en binario. Para eso, necesitamos el protocolo Binius completo. Pero primero, echemos un vistazo más profundo a los campos binarios.

Campos binarios

El campo más pequeño posible es módulo aritmético 2, que es tan pequeño que podemos escribir tablas de suma y multiplicación para él:

Podemos obtener campos binarios más grandes por extensión: si comenzamos con F 2 (enteros módulo 2) y luego definimos x donde x al cuadrado = x + 1, obtenemos las siguientes tablas de suma y multiplicación:

Resulta que podemos extender campos binarios a tamaños arbitrariamente grandes repitiendo esta construcción. A diferencia de los números complejos sobre los números reales, donde puedes agregar un nuevo elemento pero nunca agregar más elementos I (los cuaterniones existen, pero son matemáticamente extraños, por ejemplo, ab no es igual a ba), con campos finitos puedes agregar nuevas extensiones para siempre. Específicamente, nuestra definición de elemento es la siguiente: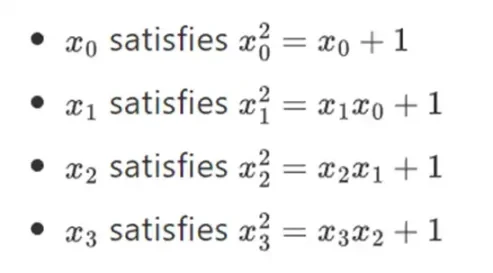

Y así sucesivamente... Esto a menudo se llama construcción de torre, porque se puede considerar que cada expansión sucesiva agrega una nueva capa a la torre. Esta no es la única forma de construir campos binarios de tamaño arbitrario, pero tiene algunas ventajas únicas que explota Binius.

Podemos representar estos números como listas de bits. Por ejemplo, 1100101010001111. El primer bit representa múltiplos de 1, el segundo bit representa múltiplos de x0 y luego los siguientes bits representan múltiplos de x1: x1, x1*x0, x2, x2*x0, etc. Esta codificación es buena porque puedes desglosarla:

Esta es una notación relativamente poco común, pero me gusta representar los elementos del campo binario como números enteros, con el bit más eficiente a la derecha. Es decir, 1 = 1, x0 = 01 = 2, 1+x0 = 11 = 3, 1+x0+x2 = 11001000 = 19, y así sucesivamente. En esta representación, eso es 61779.

La suma en el campo binario es simplemente XOR (y también lo es la resta, por cierto); tenga en cuenta que esto significa x+x = 0 para cualquier x. Para multiplicar dos elementos x*y, existe un algoritmo recursivo muy simple: dividir cada número por la mitad:

Luego, divide la multiplicación:

La última parte es la única que es un poco complicada, porque hay que aplicar reglas de simplificación. Hay formas más eficientes de hacer la multiplicación, similares al algoritmo de Karatsuba y a las transformadas rápidas de Fourier, pero lo dejaré como un ejercicio para que lo descubra el lector interesado.

La división en campos binarios se realiza combinando multiplicación e inversión. El método de inversión simple pero lento es una aplicación del pequeño teorema generalizado de Fermats. También hay un algoritmo de inversión más complejo pero más eficiente que puedes encontrar aquí. Puedes usar el código aquí para jugar con la suma, multiplicación y división de campos binarios.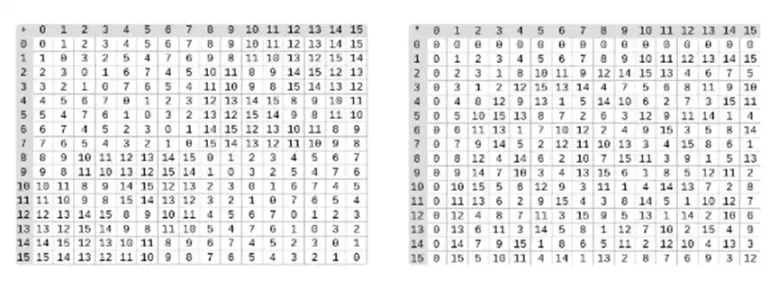

Izquierda: tabla de suma para elementos de campo binario de cuatro bits (es decir, solo 1, x 0, x 1, x 0x 1). Derecha: Tabla de multiplicar para elementos de campo binarios de cuatro bits.

La belleza de este tipo de campo binario es que combina algunas de las mejores partes de los números enteros regulares y la aritmética modular. Al igual que los números enteros normales, los elementos de los campos binarios no tienen límites: puedes crecer tanto como quieras. Pero al igual que la aritmética modular, si opera con valores dentro de un cierto límite de tamaño, todos sus resultados permanecerán en el mismo rango. Por ejemplo, si llevas 42 a potencias sucesivas, obtienes:

Después de 255 pasos, regresa a 42 elevado a 255 = 1, y al igual que los números enteros positivos y las operaciones modulares, obedecen las leyes habituales de las matemáticas: a*b=b*a, a*(b+c)= a*b+a*c, e incluso algunas leyes nuevas y extrañas.

Finalmente, los campos binarios son convenientes para manipular bits: si haces cálculos con números que caben en 2k, entonces toda tu salida también cabe en 2k bits. Esto evita incomodidades. En Ethereums EIP-4844, los bloques individuales de un blob deben ser números módulo 52435875175126190479447740508185965837690552500527637822603658699938581184513, por lo que codificar datos binarios requiere desechar algo de espacio y realizar comprobaciones adicionales en la aplicación. capa para garantizar que el valor almacenado en cada elemento sea inferior a 2248. Esto También significa que las operaciones de campo binario son súper rápidas en las computadoras, tanto en CPU como en diseños FPGA y ASIC teóricamente óptimos.

Todo esto significa que podemos realizar la codificación Reed-Solomon como lo hicimos anteriormente, de una manera que evita por completo la explosión de enteros como vimos en nuestro ejemplo, y de una manera muy nativa, el tipo de cálculos en los que las computadoras son buenas. La propiedad de división de los campos binarios (cómo podemos hacer 1100101010001111 = 11001010 + 10001111*x 3 y luego dividirlo según sea necesario) también es crucial para permitir mucha flexibilidad.

Binius completo

Ver aquí para una implementación del protocolo en Python.

Ahora podemos pasar al “Binius completo”, que adapta el “Binius simple” para (i) trabajar en campos binarios y (ii) permitirnos confirmar bits individuales. Este protocolo es difícil de entender porque alterna entre diferentes formas de ver matrices de bits; Ciertamente me llevó más tiempo entenderlo de lo que normalmente me lleva entender los protocolos criptográficos. Pero una vez que entiendes los campos binarios, la buena noticia es que las “matemáticas más difíciles” en las que se basa Binius no existen. Estos no son pares de curvas elípticas, donde hay madrigueras de geometría algebraica cada vez más profundas por las que bajar; aquí, sólo tienes campos binarios.

Veamos nuevamente el gráfico completo:

A estas alturas ya debería estar familiarizado con la mayoría de los componentes. La idea de aplanar un hipercubo en una cuadrícula, la idea de calcular combinaciones de filas y columnas como productos tensoriales de puntos de evaluación, y la idea de verificar la equivalencia entre la expansión de Reed-Solomon y luego calcular las combinaciones de filas y calcular las combinaciones de filas y luego la expansión de Reed-Solomon Todos están implementados en Binius simple.

¿Qué hay de nuevo en Binius Completo? Básicamente tres cosas:

• Los valores individuales en el hipercubo y el cuadrado deben ser bits (0 o 1).

• El proceso de expansión expande los bits en más bits agrupándolos en columnas y asumiendo temporalmente que son elementos de un campo más grande.

• Después del paso de combinación de filas, hay un paso de descomposición por elementos en bits que convierte la expansión nuevamente en bits.

Analizaremos ambos casos por turno. En primer lugar, el nuevo procedimiento de prórroga. Los códigos Reed-Solomon tienen una limitación fundamental: si desea extender n a k*n, debe trabajar en un campo con k*n valores diferentes que puedan usarse como coordenadas. Con F 2 (también conocido como bits), no puedes hacer eso. Entonces, lo que hacemos es empaquetar elementos adyacentes de F 2 para formar valores más grandes. En el ejemplo aquí, empaquetamos dos bits a la vez en los elementos { 0 , 1 , 2 , 3 } , lo cual es suficiente para nosotros ya que nuestra extensión solo tiene cuatro puntos de cálculo. En una prueba real, podríamos retroceder 16 bits a la vez. Luego ejecutamos el código Reed-Solomon en estos valores empaquetados y los descomprimimos nuevamente en bits.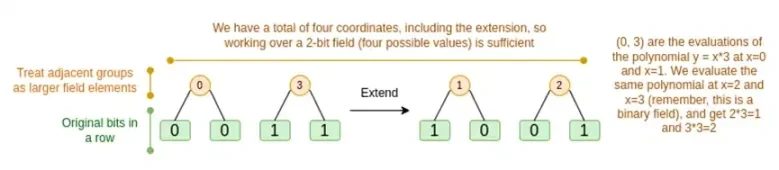

Ahora, combinaciones de filas. Para que la evaluación en un punto aleatorio sea criptográficamente segura, necesitamos muestrear ese punto desde un espacio bastante grande (mucho más grande que el propio hipercubo). Entonces, si bien el punto dentro del hipercubo es el bit, el valor calculado fuera del hipercubo será mucho mayor. En el ejemplo anterior, la combinación de filas termina siendo [11, 4, 6, 1].

Esto presenta un problema: sabemos cómo agrupar bits en un valor mayor y luego realizar una expansión de Reed-Solomon sobre ese valor, pero ¿cómo hacemos lo mismo para pares de valores más grandes?

El truco de Binius consiste en hacerlo poco a poco: miramos un solo bit de cada valor (por ejemplo, para lo que etiquetamos 11, eso es [1, 1, 0, 1]), y luego lo expandimos fila por fila. Es decir, lo expandimos en la fila 1 de cada elemento, luego en la fila x0, luego en la fila x1, luego en la fila x0x1, y así sucesivamente (bueno, en nuestro ejemplo de juguete nos detenemos ahí, pero en un caso real implementación subiríamos a 128 filas (la última sería x6*…*x0))

revisar:

• Convertimos los bits del hipercubo en una cuadrícula.

• Luego tratamos grupos de bits adyacentes en cada fila como elementos de un campo más grande y realizamos operaciones aritméticas con ellos para que Reed-Solomon expanda la fila.

• Luego tomamos la combinación de filas de cada columna de bits y obtenemos la columna de bits para cada fila como salida (mucho más pequeña para cuadrados mayores que 4 x 4)

• Luego, consideramos la salida como una matriz y sus bits como filas.

¿Por qué está pasando esto? En matemáticas normales, si comienzas a dividir un número poco a poco, la capacidad (habitual) de realizar operaciones lineales en cualquier orden y obtener el mismo resultado se desmorona. Por ejemplo, si empiezo con el número 345 y lo multiplico por 8, luego por 3, obtengo 8280, y si hago esas dos operaciones a la inversa, también obtengo 8280. Pero si inserto una operación de corte de bits entre los dos pasos, se descompone: si haces 8x, luego 3x, obtienes: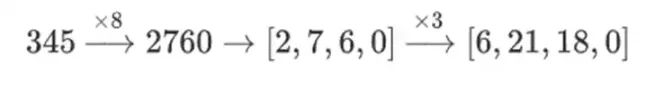

Pero si haces 3x, luego 8x, obtienes:

Pero en campos binarios construidos con estructuras de torre, este enfoque sí funciona. La razón es su separabilidad: si multiplicas un valor grande por un valor pequeño, lo que sucede en cada segmento permanece en cada segmento. Si multiplicamos 1100101010001111 por 11, esto es lo mismo que la primera descomposición de 1100101010001111, que es

Luego multiplica cada componente por 11.

Poniendolo todo junto

En general, los sistemas de prueba de conocimiento cero funcionan haciendo declaraciones sobre un polinomio que representan declaraciones sobre la evaluación subyacente al mismo tiempo: tal como vimos en el ejemplo de Fibonacci, F(X+ 2)-F(X+ 1)-F( X) = Z(X)*H(X) mientras verifica todos los pasos del cálculo de Fibonacci. Verificamos afirmaciones sobre el polinomio demostrando la evaluación en puntos aleatorios. Esta verificación de puntos aleatorios representa una verificación de todo el polinomio: si la ecuación del polinomio no coincide, existe una pequeña posibilidad de que coincida en una coordenada aleatoria específica.

En la práctica, una fuente importante de ineficiencia es que en los programas reales, la mayoría de los números con los que tratamos son pequeños: índices en bucles for, valores Verdadero/Falso, contadores y cosas así. Sin embargo, cuando ampliamos los datos con codificación Reed-Solomon para proporcionar la redundancia necesaria para que las comprobaciones basadas en Merkle sean seguras, la mayoría de los valores adicionales terminan ocupando todo el tamaño del campo, incluso si el valor original era pequeño.

Para solucionar este problema, queremos que este campo sea lo más pequeño posible. Plonky 2 nos llevó de números de 256 bits a números de 64 bits, y luego Plonky 3 lo redujo aún más a 31 bits. Pero ni siquiera eso es óptimo. Con los campos binarios, podemos trabajar con bits individuales. Esto hace que la codificación sea densa: si sus datos subyacentes reales tienen n bits, entonces su codificación tendrá n bits y la expansión tendrá 8*n bits, sin sobrecarga adicional.

Ahora, veamos este gráfico por tercera vez:

En Binius trabajamos con un polinomio multilineal: un hipercubo P(x0, x1,…xk) donde las evaluaciones individuales P(0, 0, 0, 0), P(0, 0, 0, 1) hasta P( 1, 1, 1, 1), contiene los datos que nos interesan. Para probar un cálculo en un punto determinado, reinterpretamos los mismos datos como un cuadrado. Luego ampliamos cada fila, utilizando la codificación Reed-Solomon para proporcionar la redundancia de datos necesaria para la seguridad contra consultas aleatorias de sucursales de Merkle. Luego calculamos combinaciones lineales aleatorias de las filas, diseñando los coeficientes de modo que la nueva fila combinada contenga realmente el valor calculado que nos interesa. Esta fila recién creada (reinterpretada como una fila de 128 bits) y algunas columnas seleccionadas aleatoriamente con ramas Merkle se pasan al verificador.

Luego, el verificador realiza la combinación de filas extendidas (o más precisamente, las columnas extendidas) y la combinación de filas extendidas y verifica que ambas coincidan. Luego calcula una combinación de columnas y verifica que devuelva el valor reclamado por el probador. Este es nuestro sistema de prueba (o más precisamente, el esquema de compromiso polinomial, que es un componente clave del sistema de prueba).

¿Qué no hemos cubierto todavía?

• Se requiere un algoritmo eficiente para expandir las filas para que el validador sea computacionalmente eficiente. Usamos la Transformada Rápida de Fourier en campos binarios, que se describe aquí (aunque la implementación exacta será diferente, ya que esta publicación usa una construcción menos eficiente que no se basa en la expansión recursiva).

• Aritméticamente. Los polinomios univariados son convenientes porque puedes hacer cosas como F(X+2)-F(X+1)-F(X) = Z(X)*H(X) para vincular pasos adyacentes en el cálculo. En el hipercubo, el siguiente paso está mucho menos explicado que X+1. Puedes hacer X+k, potencias de k, pero este comportamiento de salto sacrifica muchas de las ventajas clave de Binius. El artículo de Binius describe la solución. Véase la Sección 4.3), pero esto es en sí mismo un profundo agujero de conejo.

• Cómo realizar comprobaciones de valores específicos de forma segura. El ejemplo de Fibonacci requirió verificar condiciones de contorno clave: los valores de F(0)=F(1)=1 y F(100). Pero para el Binius original, no es seguro realizar comprobaciones en puntos de cálculo conocidos. Hay algunas formas bastante sencillas de convertir verificaciones de cálculos conocidos en verificaciones de cálculos desconocidos, utilizando los llamados protocolos de verificación de sumas; pero no los cubriremos aquí.

• Los protocolos de búsqueda, otra tecnología que se ha utilizado ampliamente recientemente, se utilizan para crear sistemas de prueba súper eficientes. Binius se puede utilizar junto con protocolos de búsqueda para muchas aplicaciones.

• Más allá del tiempo de verificación de la raíz cuadrada. Las raíces cuadradas son caras: una prueba de Binius de 2^32 bits tiene aproximadamente 11 MB de longitud. Puede compensar esto utilizando otros sistemas de prueba para realizar pruebas de Binius, lo que le brindará la eficiencia de una prueba de Binius con un tamaño de prueba más pequeño. Otra opción es el protocolo FRI-Binius, más complejo, que crea una prueba de tamaño multilogarítmico (al igual que el FRI normal).

• Cómo afecta Binius la compatibilidad con SNARK. El resumen básico es que si usa Binius, ya no tendrá que preocuparse por hacer cálculos aritméticos: el hash regular ya no es más eficiente que el hash aritmético tradicional, la multiplicación módulo 2 elevado a 32 o módulo 2 elevado a 256 ya no es tan doloroso como la multiplicación módulo 2, etc. Pero este es un tema complejo. Muchas cosas cambian cuando todo se hace en binario.

Espero ver más mejoras en la tecnología de prueba basada en campos binarios en los próximos meses.

Este artículo proviene de Internet: Vitalik: Binius, pruebas eficientes para campos binarios

Relacionado: BNB Coin muestra signos de recuperación: nuevo máximo anual a la vista

En resumen, el precio del BNB se recuperó de $550 y se acercó un poco más a romper la resistencia de $593. Los indicadores de precios han recuperado el impulso alcista, lo que respalda una subida de 8%. El ratio de Sharpe en 4,03 probablemente impulsará a nuevos inversores hacia el token de intercambio. Marzo fue un mes favorable para BNB Coin, ya que la criptomoneda alcanzó dos nuevos máximos para el año en tan solo unos días antes de experimentar una corrección. Después de un período de recuperación de casi dos semanas, BNB Coin está mostrando signos de alcanzar potencialmente un nuevo máximo en 2024. Pero, ¿se puede alcanzar ese hito? BNB parece prometedor Tras un rebote desde el nivel de soporte $550, el valor de BNB Coin ha aumentado a $581 en el momento de este análisis. Esta mejora refleja una recuperación en el perfil riesgo-retorno de la altcoin,…