Vitalik: Binius, effiziente Beweise für binäre Körper

Originalartikel von: Vitalik Buterin

Originalübersetzung: Kate, MarsBit

Dieser Beitrag richtet sich in erster Linie an Leser, die sich allgemein mit der Kryptografie des Jahres 2019 und insbesondere mit SNARKs und STARKs auskennen. Falls nicht, empfehle ich, diese zuerst zu lesen. Besonderer Dank geht an Justin Drake, Jim Posen, Benjamin Diamond und Radi Cojbasic für ihr Feedback und ihre Kommentare.

Over the past two years, STARKs have become a key and irreplaceable technology for efficiently making easily verifiable cryptographic proofs of very complex statements (e.g. proving that an Ethereum block is valid). One of the key reasons for this is the small field size: SNARKs based on elliptic curves require you to work on 256-bit integers to be secure enough, while STARKs allow you to use much smaller field sizes with greater efficiency: first the Goldilocks field (64-bit integer), then Mersenne 31 and BabyBear (both 31 bits). Due to these efficiency gains, Plonky 2 using Goldilocks is hundreds of times faster than its predecessors at proving many kinds of computations.

Eine naheliegende Frage ist: Können wir diesen Trend zu seinem logischen Schluss führen und Beweissysteme bauen, die schneller laufen, indem sie direkt auf Nullen und Einsen operieren? Genau das versucht Binius, indem er eine Reihe mathematischer Tricks verwendet, die ihn stark von SNARKs und STARKs von vor drei Jahren unterscheiden. Dieser Beitrag beschreibt, warum kleine Felder die Beweisgenerierung effizienter machen, warum binäre Felder einzigartig leistungsfähig sind und welche Tricks Binius verwendet, um Beweise auf binären Feldern so effizient zu machen.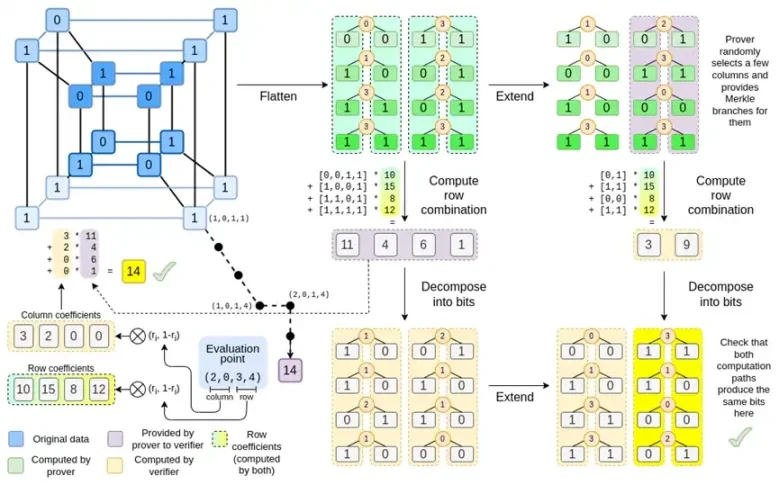

Binius, am Ende dieses Beitrags sollten Sie in der Lage sein, jeden Teil dieses Diagramms zu verstehen.

Rezension: Endliche Körper

Eine der Hauptaufgaben kryptografischer Beweissysteme besteht darin, große Datenmengen zu verarbeiten und dabei die Zahlen klein zu halten. Wenn Sie eine Aussage über ein großes Programm in eine mathematische Gleichung mit wenigen Zahlen komprimieren können, diese Zahlen aber so groß sind wie das ursprüngliche Programm, haben Sie nichts gewonnen.

Um komplexe Arithmetik durchzuführen und dabei die Zahlen klein zu halten, verwenden Kryptographen oft modulare Arithmetik. Wir wählen einen Primzahlmodul p. Der %-Operator bedeutet, den Rest zu nehmen: 15% 7 = 1, 53% 10 = 3 und so weiter. (Beachten Sie, dass die Antwort immer nicht negativ ist, also zum Beispiel -1% 10 = 9)

Sie haben modulare Arithmetik vielleicht schon einmal im Zusammenhang mit der Addition und Subtraktion von Zeit erlebt (z. B.: Wie spät ist es 4 Stunden nach 9?). Aber hier addieren und subtrahieren wir nicht nur modulo eine Zahl; wir können auch multiplizieren, dividieren und Exponenten bilden.

Wir definieren neu: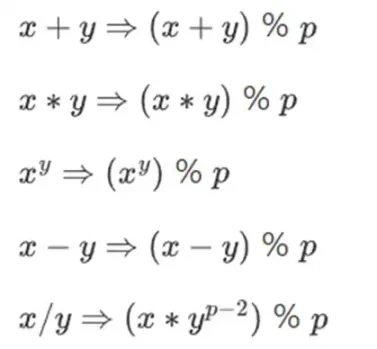

Die obigen Regeln sind alle selbstkonsistent. Wenn beispielsweise p = 7 ist, dann gilt:

5 + 3 = 1 (weil 8% 7 = 1)

1-3 = 5 (weil -2% 7 = 5)

2* 5 = 3

3/5 = 2

Ein allgemeinerer Begriff für solche Strukturen ist „finite Körper“. Ein finiter Körper ist eine mathematische Struktur, die den üblichen Gesetzen der Arithmetik folgt, bei der jedoch die Anzahl der möglichen Werte endlich ist, sodass jeder Wert durch eine feste Größe dargestellt werden kann.

Modulare Arithmetik (oder Primkörper) ist der häufigste Typ von endlichen Körpern, aber es gibt noch einen anderen Typ: Erweiterungskörper. Sie haben vielleicht schon einen Erweiterungskörper gesehen: die komplexen Zahlen. Wir stellen uns ein neues Element vor, benennen es mit i und führen eine mathematische Berechnung damit durch: (3i+2)*(2i+4)=6i*i+12i+4i+8=16i+2. Dasselbe können wir mit der Erweiterung des Primkörpers machen. Wenn wir mit kleineren Körpern arbeiten, wird die Erweiterung von Primkörpern für die Sicherheit immer wichtiger, und binäre Körper (von Binius verwendet) sind für ihren praktischen Nutzen vollständig auf die Erweiterung angewiesen.

Rezension: Arithmetik

Mit SNARKs und STARKs lassen sich Computerprogramme auf arithmetische Weise beweisen: Man nimmt eine Aussage über das Programm, das man beweisen möchte, und wandelt sie in eine mathematische Gleichung um, die ein Polynom enthält. Eine gültige Lösung der Gleichung entspricht einer gültigen Ausführung des Programms.

Nehmen wir als einfaches Beispiel an, ich habe die 100. Fibonacci-Zahl berechnet und möchte Ihnen beweisen, was sie ist. Ich erstelle ein Polynom F, das die Fibonacci-Folge kodiert: also F(0)=F(1)=1, F(2)=2, F(3)=3, F(4)=5 und so weiter für 100 Schritte. Die Bedingung, die ich beweisen muss, ist, dass F(x+2)=F(x)+F(x+1) über den gesamten Bereich x={0, 1…98}. Ich kann Sie überzeugen, indem ich Ihnen den Quotienten gebe:

wobei Z(x) = (x-0) * (x-1) * …(x-98). . Wenn ich nachweisen kann, dass F und H diese Gleichung erfüllen, dann muss F im Bereich F(x+ 2)-F(x+ 1)-F(x) erfüllen. Wenn ich zusätzlich überprüfe, dass für F gilt, dass F(0)=F(1)=1, dann muss F(100) tatsächlich die 100. Fibonacci-Zahl sein.

Wenn Sie etwas Komplizierteres beweisen möchten, ersetzen Sie die einfache Beziehung F(x+2) = F(x) + F(x+1) durch eine kompliziertere Gleichung, die im Wesentlichen besagt, dass F(x+1) die Ausgabe der Initialisierung einer virtuellen Maschine mit dem Zustand F(x) ist, und führen einen Rechenschritt aus. Sie können die Zahl 100 auch durch eine größere Zahl ersetzen, beispielsweise 100000000, um mehr Schritte unterzubringen.

Alle SNARKs und STARKs basieren auf der Idee, einfache Gleichungen über Polynome (und manchmal Vektoren und Matrizen) zu verwenden, um eine große Anzahl von Beziehungen zwischen einzelnen Werten darzustellen. Nicht alle Algorithmen prüfen auf Äquivalenz zwischen benachbarten Rechenschritten wie die oben genannten: PLONK beispielsweise tut dies nicht und R1CS auch nicht. Viele der effektivsten Prüfungen tun dies jedoch, da es einfacher ist, den Mehraufwand zu minimieren, indem dieselbe Prüfung (oder dieselben wenigen Prüfungen) viele Male durchgeführt wird.

Plonky 2: Von 256-Bit-SNARKs und STARKs zu 64-Bit … nur STARKs

Vor fünf Jahren lautete eine vernünftige Zusammenfassung der verschiedenen Arten von Zero-Knowledge-Beweisen wie folgt. Es gibt zwei Arten von Beweisen: (auf elliptischen Kurven basierende) SNARKs und (auf Hash basierende) STARKs. Technisch gesehen sind STARKs eine Art SNARK, aber in der Praxis ist es üblich, „SNARK“ für die auf elliptischen Kurven basierende Variante und „STARK“ für die auf Hash basierende Konstruktion zu verwenden. SNARKs sind klein, sodass Sie sie sehr schnell verifizieren und problemlos in der Kette installieren können. STARKs sind groß, erfordern jedoch kein vertrauenswürdiges Setup und sind quantenresistent.

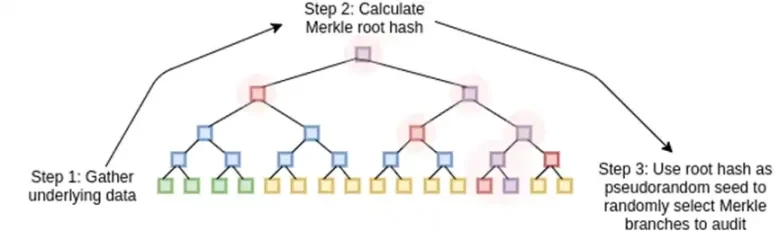
STARKs funktionieren, indem sie Daten als Polynom behandeln, die Berechnung dieses Polynoms durchführen und die Merkle-Wurzel der erweiterten Daten als „Polynom-Verpflichtung“ verwenden.

Ein wichtiger historischer Aspekt ist, dass zuerst SNARKs auf Basis elliptischer Kurven weit verbreitet waren: STARKs wurden dank FRI erst um 2018 effizient genug, und zu diesem Zeitpunkt lief Zcash bereits seit über einem Jahr. SNARKs auf Basis elliptischer Kurven haben eine wichtige Einschränkung: Wenn Sie ein SNARK auf Basis elliptischer Kurven verwenden möchten, muss die Arithmetik in diesen Gleichungen modulo der Anzahl der Punkte auf der elliptischen Kurve erfolgen. Das ist eine große Zahl, normalerweise nahe bei 2 hoch 256. Für die Kurve bn128 beträgt sie beispielsweise 21888242871839275222246405745257275088548364400416034343698204186575808495617. In der realen Computertechnik werden jedoch kleine Zahlen verwendet. Wenn Sie an ein reales Programm in Ihrer bevorzugten Sprache denken, verwendet es hauptsächlich Zähler, Indizes in For-Schleifen, Positionen im Programm, einzelne Bits, die „Wahr“ oder „Falsch“ darstellen, und andere Dinge, die fast immer nur wenige Ziffern lang sind.

Selbst wenn Ihre ursprünglichen Daten aus kleinen Zahlen bestehen, erfordert der Beweisprozess die Berechnung von Quotienten, Erweiterungen, zufälligen linearen Kombinationen und anderen Datentransformationen, die zu einer gleichen oder größeren Anzahl von Objekten führen, die im Durchschnitt so groß sind wie die Gesamtgröße Ihres Felds. Dies führt zu einer entscheidenden Ineffizienz: Um eine Berechnung mit n kleinen Werten zu beweisen, müssen Sie viel mehr Berechnungen mit n viel größeren Werten durchführen. Ursprünglich übernahmen STARKs die SNARK-Gewohnheit, 256-Bit-Felder zu verwenden, und litten daher unter derselben Ineffizienz.

Reed-Solomon-Erweiterung einer Polynomauswertung. Obwohl der ursprüngliche Wert klein ist, werden die zusätzlichen Werte auf die volle Größe des Feldes erweitert (in diesem Fall 2^31 – 1).

Im Jahr 2022 wurde Plonky 2 veröffentlicht. Die wichtigste Neuerung von Plonky 2 besteht darin, Arithmetik modulo einer kleineren Primzahl durchzuführen: 2 hoch 64 – 2 hoch 32 + 1 = 18446744067414584321. Jetzt kann jede Addition oder Multiplikation immer mit wenigen Anweisungen auf der CPU durchgeführt werden, und das Hashen aller Daten zusammen ist 4-mal schneller als zuvor. Es gibt jedoch ein Problem: Diese Methode funktioniert nur für STARKs. Wenn Sie versuchen, SNARKs zu verwenden, werden elliptische Kurven für so kleine elliptische Kurven unsicher.

Um die Sicherheit zu gewährleisten, muss Plonky 2 auch Erweiterungsfelder einführen. Eine Schlüsseltechnik zum Überprüfen arithmetischer Gleichungen ist die zufällige Punktauswahl: Wenn Sie überprüfen möchten, ob H(x) * Z(x) gleich F(x+ 2)-F(x+ 1)-F(x) ist, können Sie eine Koordinate r zufällig auswählen, eine polynomische Verpflichtung zum Beweis von H(r), Z(r), F(r), F(r+ 1) und F(r+ 2) bereitstellen und dann überprüfen, ob H(r) * Z(r) gleich F(r+ 2)-F(r+ 1)- F(r) ist. Wenn ein Angreifer die Koordinaten im Voraus erraten kann, kann er das Beweissystem täuschen – aus diesem Grund muss das Beweissystem zufällig sein. Dies bedeutet aber auch, dass die Koordinaten aus einer ausreichend großen Menge ausgewählt werden müssen, damit der Angreifer sie nicht zufällig erraten kann. Dies trifft offensichtlich zu, wenn der Modul nahe bei 2 hoch 256 liegt. Beim Modul 2^64 – 2^32 + 1 sind wir jedoch noch nicht so weit, und dies trifft sicher nicht zu, wenn wir bis zu 2^31 – 1 herunterkommen. Ein Angreifer kann durchaus zwei Milliarden Mal versuchen, einen Beweis zu fälschen, bis er Glück hat.

Um dies zu verhindern, entnehmen wir r einem erweiterten Feld, sodass Sie beispielsweise y definieren können, wobei y^3 = 5 ist, und Kombinationen aus 1, y und y^2 nehmen können. Dadurch beträgt die Gesamtzahl der Koordinaten etwa 2^93. Die meisten der vom Beweiser berechneten Polynome gehen nicht in dieses erweiterte Feld; es sind nur ganze Zahlen modulo 2^31-1, sodass Sie immer noch die gesamte Effizienz aus der Verwendung eines kleinen Felds erhalten. Aber zufällige Punktprüfungen und FRI-Berechnungen greifen auf dieses größere Feld zu, um die erforderliche Sicherheit zu erreichen.

Von kleinen Primzahlen zu Binärzahlen

Computer führen Arithmetik durch, indem sie größere Zahlen als Folgen von Nullen und Einsen darstellen und Schaltkreise auf der Basis dieser Bits aufbauen, um Operationen wie Addition und Multiplikation zu berechnen. Computer sind besonders für 16-, 32- und 64-Bit-Ganzzahlen optimiert. Beispielsweise wurden 2^64 – 2^32 + 1 und 2^31 – 1 nicht nur gewählt, weil sie in diese Grenzen passen, sondern auch, weil sie gut in diese Grenzen passen: Eine Multiplikation modulo 2^64 – 2^32 + 1 kann durch eine normale 32-Bit-Multiplikation und bitweises Verschieben und Kopieren der Ausgabe an einigen Stellen durchgeführt werden; dieser Artikel erklärt einige der Tricks gut.

Ein viel besserer Ansatz wäre jedoch, die Berechnungen direkt im Binärsystem durchzuführen. Was wäre, wenn die Addition einfach XOR sein könnte, ohne dass man sich um den Übertrag von 1 + 1 von einem Bit zum nächsten sorgen müsste? Was wäre, wenn die Multiplikation auf die gleiche Weise stärker parallelisiert werden könnte? Diese Vorteile basieren alle auf der Möglichkeit, wahre/falsche Werte mit einem einzigen Bit darstellen zu können.

Diese Vorteile einer direkten Binärberechnung zu nutzen, ist genau das, was Binius versucht. Das Binius-Team demonstrierte die Effizienzgewinne in seiner Präsentation auf dem zkSummit:

Obwohl die Größe von 32-Bit-Binärfeldern etwa gleich ist, erfordern Operationen an binären 32-Bit-Feldern fünfmal weniger Rechenressourcen als Operationen an 31-Bit-Mersenne-Feldern.

Von univariaten Polynomen zu Hyperwürfeln

Angenommen, wir glauben dieser Argumentation und möchten alles mit Bits (0 und 1) machen. Wie können wir eine Milliarde Bits mit einem einzigen Polynom darstellen?

Hier stehen wir vor zwei praktischen Problemen:

1. Damit ein Polynom eine große Anzahl von Werten darstellen kann, müssen diese Werte bei der Auswertung des Polynoms zugänglich sein: im obigen Fibonacci-Beispiel F(0), F(1) … F(100), und bei einer größeren Berechnung werden die Exponenten Millionen betragen. Die von uns verwendeten Felder müssen Zahlen dieser Größe enthalten.

2. Um einen Wert zu beweisen, den wir in einem Merkle-Baum (wie bei allen STARKs) angeben, ist eine Reed-Solomon-Kodierung erforderlich: zum Beispiel die Erweiterung der Werte von n auf 8n unter Verwendung von Redundanz, um zu verhindern, dass böswillige Beweiser betrügen, indem sie während der Berechnung einen Wert fälschen. Dies erfordert auch ein ausreichend großes Feld: Um von einer Million Werten auf 8 Millionen zu erweitern, benötigen Sie 8 Millionen verschiedene Punkte, um das Polynom auszuwerten.

Eine Schlüsselidee von Binius besteht darin, diese beiden Probleme getrennt zu lösen, und zwar indem dieselben Daten auf zwei verschiedene Arten dargestellt werden. Zunächst die Polynome selbst. Systeme wie SNARKs auf Basis elliptischer Kurven, STARKs aus dem Jahr 2019, Plonky 2 und andere arbeiten normalerweise mit Polynomen über einer Variablen: F(x). Binius hingegen lässt sich vom Spartan-Protokoll inspirieren und verwendet multivariate Polynome: F(x 1, x 2,… xk). Tatsächlich stellen wir die gesamte Berechnungskurve auf einem Berechnungshyperwürfel dar, wobei jedes xi entweder 0 oder 1 ist. Wenn wir beispielsweise eine Fibonacci-Folge darstellen möchten und dennoch ein Feld verwenden, das groß genug ist, um sie darzustellen, können wir uns ihre ersten 16 Folgen wie folgt vorstellen: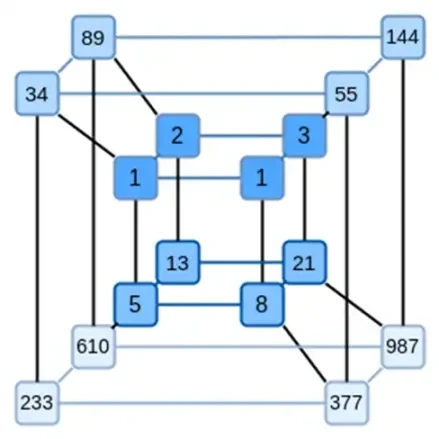

Das heißt, F(0,0,0,0) sollte 1 sein, F(1,0,0,0) ist ebenfalls 1, F(0,1,0,0) ist 2 und so weiter, bis hin zu F(1,1,1,1) = 987. Bei einem solchen Hyperwürfel von Berechnungen gibt es ein multivariates lineares Polynom (Grad 1 in jeder Variable), das diese Berechnungen erzeugt. Wir können uns also vorstellen, dass dieser Wertesatz das Polynom darstellt; wir müssen die Koeffizienten nicht berechnen.

Dieses Beispiel dient natürlich nur der Veranschaulichung: In der Praxis besteht der ganze Sinn des Hyperwürfels darin, uns mit einzelnen Bits umgehen zu lassen. Die Binius-eigene Methode zum Berechnen von Fibonacci-Zahlen besteht darin, einen höherdimensionalen Würfel zu verwenden, der eine Zahl pro Gruppe von beispielsweise 16 Bits speichert. Dies erfordert einiges Geschick, um die Addition ganzer Zahlen auf Bitbasis zu implementieren, aber für Binius ist es nicht allzu schwer.

Sehen wir uns nun die Löschcodes an. STARKs funktionieren so, dass man n Werte nimmt, sie nach Reed-Solomon-Prinzip auf weitere Werte erweitert (normalerweise 8n, normalerweise zwischen 2n und 32n), dann zufällig einige Merkle-Zweige aus der Erweiterung auswählt und eine Art Prüfung an ihnen durchführt. Der Hyperwürfel hat in jeder Dimension die Länge 2. Daher ist es nicht praktikabel, ihn direkt zu erweitern: Es ist nicht genug Platz vorhanden, um Merkle-Zweige aus 16 Werten abzutasten. Wie machen wir es also? Nehmen wir an, der Hyperwürfel ist quadratisch!

Einfacher Binius – Ein Beispiel

Sehen Hier für eine Python-Implementierung des Protokolls.

Schauen wir uns ein Beispiel an, bei dem wir der Einfachheit halber normale Ganzzahlen als Felder verwenden (in einer echten Implementierung würden wir binäre Feldelemente verwenden). Zuerst kodieren wir den Hyperwürfel, den wir übermitteln möchten, als Quadrat:

Nun erweitern wir das Quadrat mit der Reed-Solomon-Methode. Das heißt, wir behandeln jede Zeile als Polynom dritten Grades, das bei x = { 0, 1, 2, 3 } ausgewertet wird, und werten dasselbe Polynom bei x = { 4, 5, 6, 7 } aus: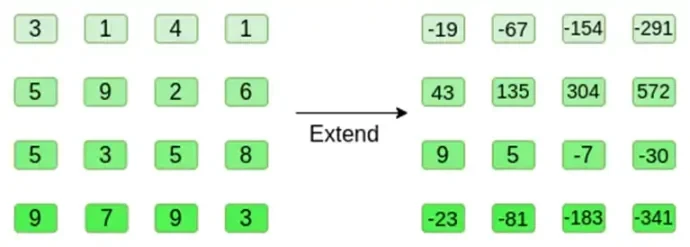

Beachten Sie, dass die Zahlen sehr groß werden können! Aus diesem Grund verwenden wir in praktischen Implementierungen immer endliche Körper statt normaler Ganzzahlen: Wenn wir beispielsweise Ganzzahlen modulo 11 verwenden, ist die Erweiterung der ersten Zeile einfach [3, 10, 0, 6].

Wenn Sie die Erweiterung ausprobieren und die Zahlen selbst überprüfen möchten, können Sie hier meinen einfachen Reed-Solomon-Erweiterungscode verwenden.

Als nächstes behandeln wir diese Erweiterung als Spalte und erstellen einen Merkle-Baum der Spalte. Die Wurzel des Merkle-Baums ist unser Commitment.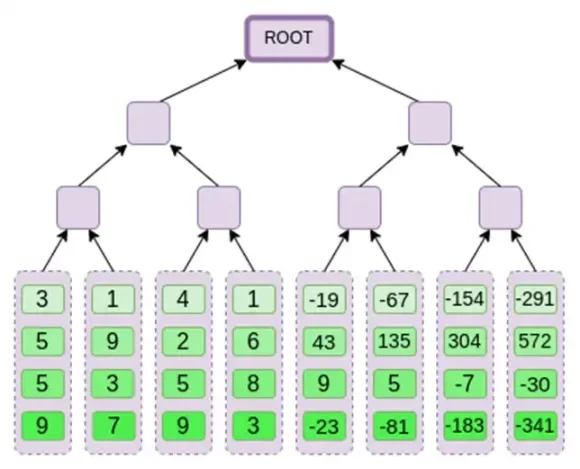

Nehmen wir nun an, dass der Beweiser die Berechnung dieses Polynoms r = {r 0, r 1, r 2, r 3 } an einem bestimmten Punkt beweisen möchte. Es gibt einen subtilen Unterschied in Binius, der es schwächer macht als andere polynomische Commitment-Schemata: Der Beweiser sollte s nicht kennen oder erraten können, bevor er sich auf die Merkle-Wurzel festlegt (mit anderen Worten, r sollte ein pseudozufälliger Wert sein, der von der Merkle-Wurzel abhängt). Dies macht das Schema für Datenbanksuchen nutzlos (z. B., ok, Sie haben mir die Merkle-Wurzel gegeben, jetzt beweisen Sie mir P(0, 0, 1, 0)!). Aber die Zero-Knowledge-Beweisprotokolle, die wir tatsächlich verwenden, erfordern normalerweise keine Datenbanksuchen; sie erfordern nur die Überprüfung des Polynoms an einem zufälligen Auswertungspunkt. Diese Einschränkung dient also unseren Zwecken.

Angenommen, wir wählen r = { 1, 2, 3, 4 } (das Polynom ergibt -137; Sie können dies mit diesem Code bestätigen). Nun kommen wir zum Beweis. Wir teilen r in zwei Teile auf: Der erste Teil { 1, 2 } stellt die lineare Kombination der Spalten innerhalb der Zeile dar, und der zweite Teil { 3, 4 } stellt die lineare Kombination der Zeilen dar. Wir berechnen ein Tensorprodukt und für die Spalten:

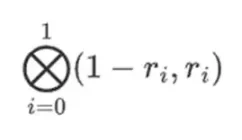
Für den Zeilenteil:

Das bedeutet: eine Liste aller möglichen Produkte eines Wertes in jedem Satz. Im Zeilenfall erhalten wir:

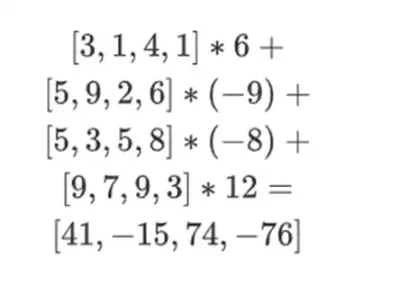
[( 1-r 2)*( 1-r 3), ( 1-r 3), ( 1-r 2)*r 3, r 2*r 3 ]

Mit r = { 1, 2, 3, 4 } (also r 2 = 3 und r 3 = 4):

[( 1-3)*( 1-4), 3*( 1-4),( 1-3)* 4, 3* 4 ] = [ 6, -9 -8 -12 ]

Nun berechnen wir eine neue Zeile t, indem wir eine lineare Kombination der vorhandenen Zeilen bilden. Das heißt, wir nehmen:

Sie können sich das, was hier passiert, als eine partielle Auswertung vorstellen. Wenn wir das vollständige Tensorprodukt mit dem vollständigen Vektor aller Werte multiplizieren würden, käme man auf die Berechnung P(1, 2, 3, 4) = -137. Hier haben wir das partielle Tensorprodukt mit nur der Hälfte der Auswertungskoordinaten multipliziert und das Raster aus N Werten auf eine einzelne Zeile aus Quadratwurzel-N-Werten reduziert. Wenn Sie diese Zeile an jemand anderen weitergeben, kann dieser den Rest der Berechnung mit dem Tensorprodukt der anderen Hälfte der Auswertungskoordinaten durchführen.

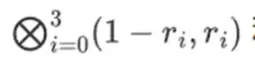
Der Beweiser liefert dem Verifizierer die folgende neue Zeile: t und einen Merkle-Beweis einiger zufällig ausgewählter Spalten. In unserem Beispiel lassen wir den Beweiser nur die letzte Spalte liefern; im wirklichen Leben müsste der Beweiser Dutzende von Spalten liefern, um eine ausreichende Sicherheit zu erreichen.

Nun nutzen wir die Linearität von Reed-Solomon-Codes. Die Schlüsseleigenschaft, die wir ausnutzen, ist, dass eine lineare Kombination von Reed-Solomon-Erweiterungen dasselbe Ergebnis liefert wie eine Reed-Solomon-Erweiterung einer linearen Kombination. Diese sequentielle Unabhängigkeit tritt normalerweise auf, wenn beide Operationen linear sind.

Der Prüfer macht genau das. Er berechnet t und berechnet lineare Kombinationen derselben Spalten, die der Beweiser zuvor berechnet hat (aber nur die vom Beweiser bereitgestellten Spalten) und prüft, ob die beiden Verfahren dieselbe Antwort liefern.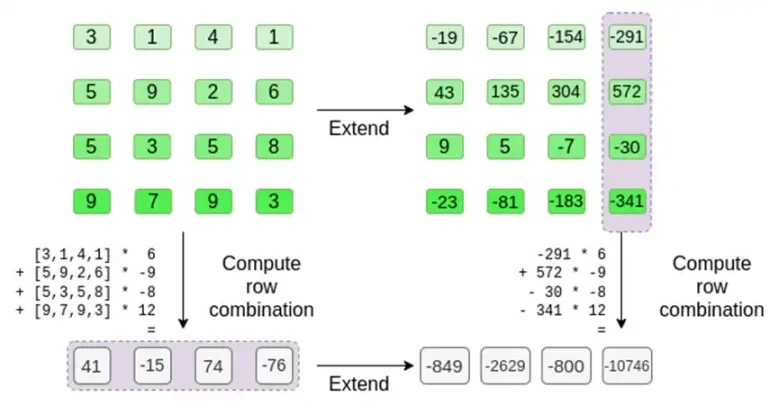

In diesem Fall erweitern wir t und berechnen dieselbe lineare Kombination ([6,-9,-8, 12]), die beide dasselbe Ergebnis liefern: -10746. Dies beweist, dass die Merkle-Wurzel in gutem Glauben konstruiert wurde (oder zumindest nahe genug kommt) und dass sie mit t übereinstimmt: Zumindest die überwiegende Mehrheit der Spalten ist miteinander kompatibel.

Aber es gibt noch eine Sache, die der Prüfer überprüfen muss: die Auswertung des Polynoms {r 0 …r 3 }. Alle bisherigen Schritte des Prüfers waren nicht wirklich von dem vom Beweiser behaupteten Wert abhängig. So überprüfen wir das. Wir nehmen das Tensorprodukt des „Spaltenteils“, den wir als Berechnungspunkt markiert haben: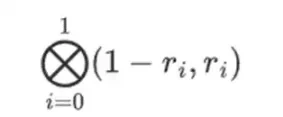

In unserem Fall, wo r = { 1, 2, 3, 4 }, also die Hälfte der ausgewählten Spalten { 1, 2 } ist, ist dies gleichbedeutend mit:

Nun nehmen wir diese Linearkombination t:

Dies ist dasselbe wie das direkte Lösen des Polynoms.

Das Obige ist eine sehr vollständige Beschreibung des einfachen Binius-Protokolls. Dieses hat bereits einige interessante Vorteile: Da die Daten beispielsweise in Zeilen und Spalten aufgeteilt sind, benötigen Sie nur ein Feld, das halb so groß ist. Allerdings werden dadurch nicht alle Vorteile der binären Berechnung erreicht. Dafür benötigen wir das vollständige Binius-Protokoll. Aber schauen wir uns zunächst die binären Felder genauer an.

Binäre Felder

Der kleinstmögliche Körper ist die Arithmetik Modulo 2, die so klein ist, dass wir Additions- und Multiplikationstabellen dafür schreiben können:

Größere Binärkörper können wir durch Erweiterung erhalten: Wenn wir mit F 2 (ganze Zahlen Modulo 2) beginnen und dann x definieren, wobei x zum Quadrat = x + 1 ist, erhalten wir die folgenden Additions- und Multiplikationstabellen:

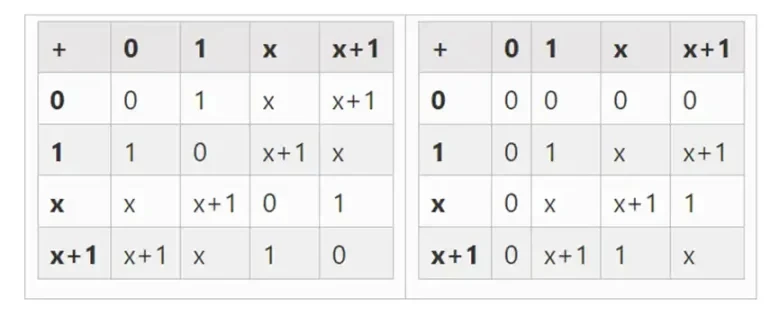
Es stellt sich heraus, dass wir binäre Körper durch Wiederholung dieser Konstruktion auf beliebig große Größen erweitern können. Anders als bei komplexen Zahlen über reellen Zahlen, wo man ein neues Element hinzufügen kann, aber nie weitere Elemente I hinzufügen kann (Quaternionen existieren zwar, aber sie sind mathematisch seltsam, z. B. ist ab nicht gleich ba), kann man bei endlichen Körpern immer neue Erweiterungen hinzufügen. Genauer gesagt lautet unsere Definition eines Elements wie folgt: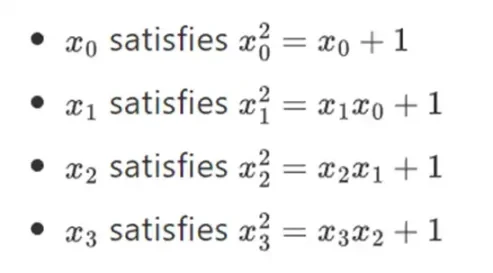

Und so weiter … Dies wird oft als Turmkonstruktion bezeichnet, da jede nachfolgende Erweiterung als Hinzufügen einer neuen Ebene zum Turm betrachtet werden kann. Dies ist nicht die einzige Möglichkeit, binäre Felder beliebiger Größe zu konstruieren, aber es bietet einige einzigartige Vorteile, die Binius ausnutzt.

Wir können diese Zahlen als Bitlisten darstellen. Zum Beispiel 1100101010001111. Das erste Bit stellt Vielfache von 1 dar, das zweite Bit stellt Vielfache von x0 dar und die folgenden Bits stellen Vielfache von x1 dar: x1, x1*x0, x2, x2*x0 und so weiter. Diese Kodierung ist praktisch, weil man sie aufschlüsseln kann:

Dies ist eine relativ unübliche Notation, aber ich stelle binäre Feldelemente gerne als Ganzzahlen dar, wobei das effizientere Bit rechts steht. Das heißt, 1 = 1, x0 = 01 = 2, 1+x0 = 11 = 3, 1+x0+x2 = 11001000 = 19 und so weiter. In dieser Darstellung ist das 61779.

Die Addition im Binärfeld ist einfach XOR (und das gilt übrigens auch für die Subtraktion); beachten Sie, dass dies für jedes x x+x = 0 bedeutet. Um zwei Elemente x*y miteinander zu multiplizieren, gibt es einen sehr einfachen rekursiven Algorithmus: Teilen Sie jede Zahl in zwei Hälften:

Dann teilen Sie die Multiplikation auf:

Der letzte Teil ist der einzige, der ein wenig knifflig ist, da Sie Vereinfachungsregeln anwenden müssen. Es gibt effizientere Möglichkeiten, die Multiplikation durchzuführen, ähnlich dem Karatsubas-Algorithmus und den Fast Fourier Transforms, aber das überlasse ich dem interessierten Leser als Übung.

Die Division in binären Körpern erfolgt durch die Kombination von Multiplikation und Inversion. Die einfache, aber langsame Inversionsmethode ist eine Anwendung des verallgemeinerten kleinen Fermatschen Theorems. Es gibt auch einen komplexeren, aber effizienteren Inversionsalgorithmus, den Sie hier finden können. Sie können den Code hier verwenden, um mit Addition, Multiplikation und Division von binären Körpern zu spielen.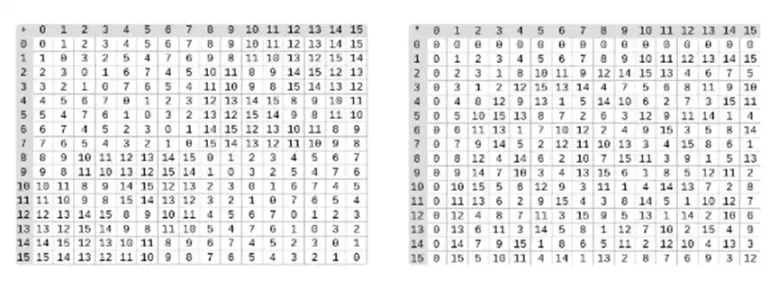

Links: Additionstabelle für vierbit binäre Feldelemente (also nur 1, x 0, x 1, x 0x 1). Rechts: Multiplikationstabelle für vierbit binäre Feldelemente.

Das Schöne an dieser Art von binärem Feld ist, dass es einige der besten Eigenschaften von regulären Ganzzahlen und modularer Arithmetik kombiniert. Wie bei regulären Ganzzahlen sind die Elemente binärer Felder unbegrenzt: Sie können sie beliebig vergrößern. Aber genau wie bei der modularen Arithmetik bleiben alle Ergebnisse im gleichen Bereich, wenn Sie mit Werten innerhalb einer bestimmten Größenbeschränkung arbeiten. Wenn Sie beispielsweise 42 potenzieren, erhalten Sie:

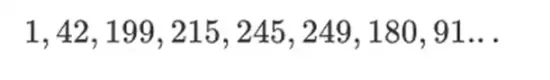
Nach 255 Schritten sind Sie wieder bei 42 hoch 255 = 1, und genau wie positive ganze Zahlen und modulare Operationen gehorchen sie den üblichen Gesetzen der Mathematik: a*b=b*a, a*(b+c)=a*b+a*c und sogar einigen merkwürdigen neuen Gesetzen.

Schließlich sind binäre Felder praktisch für die Manipulation von Bits: Wenn Sie mit Zahlen rechnen, die in 2k passen, dann passt Ihre gesamte Ausgabe auch in 2k Bits. Dies vermeidet Unannehmlichkeiten. In Ethereums EIP-4844 müssen die einzelnen Blöcke eines Blobs Zahlen modulo 52435875175126190479447740508185965837690552500527637822603658699938581184513 sein, sodass die Kodierung binärer Daten erfordert, etwas Platz zu verschwenden und zusätzliche Prüfungen auf der Anwendungsebene durchzuführen, um sicherzustellen, dass der in jedem Element gespeicherte Wert kleiner als 2248 ist. Dies bedeutet auch, dass binäre Feldoperationen auf Computern – sowohl auf CPUs als auch auf theoretisch optimalen FPGA- und ASIC-Designs – superschnell sind.

Das alles bedeutet, dass wir Reed-Solomon-Kodierung wie oben beschrieben durchführen können, und zwar auf eine Weise, die die Ganzzahlexplosion, wie wir sie in unserem Beispiel gesehen haben, vollständig vermeidet, und zwar auf eine sehr native Weise, die Art von Berechnungen, für die Computer gut geeignet sind. Die Split-Eigenschaft von binären Feldern – wie wir 1100101010001111 = 11001010 + 10001111*x 3 berechnen und dann nach Bedarf aufteilen können – ist ebenfalls entscheidend, um viel Flexibilität zu ermöglichen.

Schließe Binius ab

Sehen Hier für eine Python-Implementierung des Protokolls.

Jetzt können wir zu „Full Binius“ übergehen, das „Simple Binius“ anpasst, um (i) mit binären Feldern zu arbeiten und (ii) uns das Übertragen einzelner Bits zu ermöglichen. Dieses Protokoll ist schwer zu verstehen, da es zwischen verschiedenen Betrachtungsweisen von Bitmatrizen hin- und herschaltet. Ich habe definitiv länger gebraucht, um es zu verstehen, als ich normalerweise brauche, um kryptografische Protokolle zu verstehen. Aber wenn Sie erst einmal binäre Felder verstanden haben, ist die gute Nachricht, dass die „schwierigere Mathematik“, auf die sich Binius stützt, nicht existiert. Dies sind keine elliptischen Kurvenpaarungen, bei denen man sich immer tiefer in algebraische Geometrie vertiefen muss; hier haben Sie einfach nur binäre Felder.

Schauen wir uns das vollständige Diagramm noch einmal an:

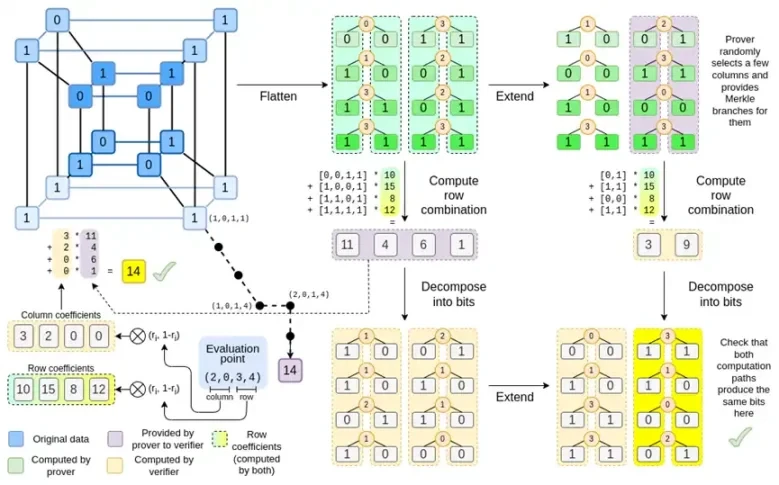
Mittlerweile sollten Sie mit den meisten Komponenten vertraut sein. Die Idee, einen Hyperwürfel in ein Raster zu glätten, die Idee, Zeilen- und Spaltenkombinationen als Tensorprodukte von Bewertungspunkten zu berechnen, und die Idee, die Äquivalenz zwischen der Reed-Solomon-Erweiterung und anschließender Berechnung von Zeilenkombinationen sowie der Berechnung von Zeilenkombinationen und anschließender Reed-Solomon-Erweiterung zu prüfen, sind alle in einfachem Binius implementiert.

Was ist neu in Complete Binius? Im Wesentlichen drei Dinge:

• Die einzelnen Werte im Hyperwürfel und Quadrat müssen Bits (0 oder 1) sein.

• Der Expansionsprozess erweitert die Bits in weitere Bits, indem er sie in Spalten gruppiert und vorübergehend davon ausgeht, dass sie Elemente eines größeren Felds sind.

• Nach dem Zeilenkombinationsschritt folgt ein Schritt zur elementweisen Zerlegung in Bits, der die Erweiterung wieder in Bits umwandelt.

Wir besprechen beide Fälle der Reihe nach. Zunächst das neue Erweiterungsverfahren. Reed-Solomon-Codes haben eine grundsätzliche Einschränkung: Wenn Sie n auf k*n erweitern wollen, müssen Sie in einem Feld mit k*n verschiedenen Werten arbeiten, die als Koordinaten verwendet werden können. Mit F2 (auch bekannt als Bits) ist das nicht möglich. Wir packen also benachbarte Elemente von F2 zusammen, um größere Werte zu bilden. In diesem Beispiel packen wir jeweils zwei Bits in die Elemente {0, 1, 2, 3}, was uns reicht, da unsere Erweiterung nur vier Berechnungspunkte hat. In einem echten Beweis könnten wir jeweils 16 Bits zurückgehen. Dann führen wir den Reed-Solomon-Code auf diesen gepackten Werten aus und packen sie wieder in Bits aus.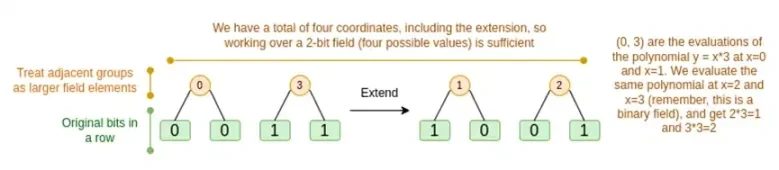

Nun zu den Zeilenkombinationen. Um die Auswertung an einem zufälligen Punkt kryptografisch sicher zu machen, müssen wir diesen Punkt aus einem ziemlich großen Raum (viel größer als der Hyperwürfel selbst) auswählen. Während also der Punkt innerhalb des Hyperwürfels das Bit ist, wird der berechnete Wert außerhalb des Hyperwürfels viel größer sein. Im obigen Beispiel ergibt sich die Zeilenkombination als [11, 4, 6, 1].

Dies stellt ein Problem dar: Wir wissen, wie man Bits zu einem größeren Wert gruppiert und dann eine Reed-Solomon-Erweiterung für diesen Wert durchführt, aber wie machen wir dasselbe für größere Wertepaare?

Binius‘ Trick besteht darin, es Stück für Stück zu machen: Wir betrachten ein einzelnes Bit jedes Wertes (z. B. für das, was wir mit 11 beschriftet haben, also [1, 1, 0, 1]) und erweitern es dann Zeile für Zeile. Das heißt, wir erweitern es in Zeile 1 jedes Elements, dann in Zeile x0, dann in Zeile x1, dann in Zeile x0x1 und so weiter (also, in unserem Spielzeugbeispiel hören wir hier auf, aber in einer echten Implementierung würden wir bis zu 128 Zeilen gehen (die letzte ist x6*…*x0)).

Rezension:

• Wir wandeln die Bits im Hyperwürfel in ein Gitter um

• Wir behandeln dann Gruppen von benachbarten Bits in jeder Zeile als Elemente eines größeren Feldes und führen arithmetische Operationen auf ihnen durch, um die Zeile nach Reed-Solomon zu erweitern

• Wir nehmen dann die Zeilenkombination jeder Bit-Spalte und erhalten die Bit-Spalte für jede Zeile als Ausgabe (viel kleiner für Quadrate, die größer als 4 x 4 sind).

• Dann betrachten wir die Ausgabe als Matrix und ihre Bits als Zeilen

Warum passiert das? Wenn man in der normalen Mathematik beginnt, eine Zahl Stück für Stück zu zerlegen, bricht die (übliche) Möglichkeit zusammen, lineare Operationen in beliebiger Reihenfolge auszuführen und das gleiche Ergebnis zu erhalten. Wenn ich beispielsweise mit der Zahl 345 beginne und sie mit 8 und dann mit 3 multipliziere, erhalte ich 8280, und wenn ich diese beiden Operationen umgekehrt ausführe, erhalte ich auch 8280. Wenn ich jedoch zwischen den beiden Schritten eine Bit-Slicing-Operation einfüge, bricht es zusammen: Wenn Sie 8x und dann 3x ausführen, erhalten Sie: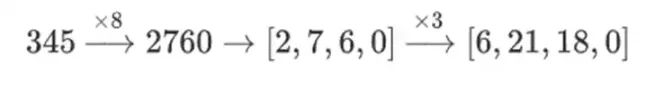

Aber wenn Sie 3x und dann 8x machen, erhalten Sie:

Aber in binären Feldern mit Turmstrukturen funktioniert dieser Ansatz. Der Grund dafür ist ihre Trennbarkeit: Wenn Sie einen großen Wert mit einem kleinen Wert multiplizieren, bleibt das, was auf jedem Segment passiert, auf jedem Segment. Wenn wir 1100101010001111 mit 11 multiplizieren, ist dies dasselbe wie die erste Zerlegung von 1100101010001111, was

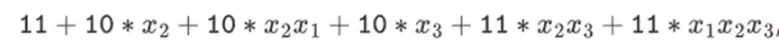
Dann multiplizieren Sie jede Komponente mit 11.

Alles zusammenfügen

Im Allgemeinen funktionieren Zero-Knowledge-Beweissysteme, indem sie Aussagen über ein Polynom treffen, die gleichzeitig Aussagen über die zugrundeliegende Auswertung darstellen: genau wie wir es im Fibonacci-Beispiel gesehen haben, F(X+ 2)-F(X+ 1)-F(X) = Z(X)*H(X), während alle Schritte der Fibonacci-Berechnung überprüft werden. Wir überprüfen Aussagen über das Polynom, indem wir die Auswertung an zufälligen Punkten beweisen. Diese Überprüfung der zufälligen Punkte stellt eine Überprüfung des gesamten Polynoms dar: Wenn die Polynomgleichung nicht übereinstimmt, besteht eine kleine Chance, dass sie an einer bestimmten zufälligen Koordinate übereinstimmt.

In der Praxis ist eine der Hauptursachen für Ineffizienzen, dass in echten Programmen die meisten Zahlen, mit denen wir arbeiten, klein sind: Indizes in For-Schleifen, True/False-Werte, Zähler und dergleichen. Wenn wir Daten jedoch mit Reed-Solomon-Kodierung erweitern, um die Redundanz bereitzustellen, die erforderlich ist, um auf Merkle basierende Prüfungen sicher zu machen, nehmen die meisten zusätzlichen Werte am Ende die gesamte Größe des Felds ein, selbst wenn der ursprüngliche Wert klein war.

Um dies zu beheben, möchten wir dieses Feld so klein wie möglich machen. Plonky 2 brachte uns von 256-Bit-Zahlen auf 64-Bit-Zahlen, und Plonky 3 reduzierte es weiter auf 31 Bit. Aber selbst das ist nicht optimal. Bei binären Feldern können wir mit einzelnen Bits umgehen. Dies macht die Kodierung dicht: Wenn Ihre eigentlichen zugrunde liegenden Daten n Bits haben, dann hat Ihre Kodierung n Bits und die Erweiterung hat 8*n Bits, ohne zusätzlichen Overhead.

Schauen wir uns dieses Diagramm nun ein drittes Mal an:

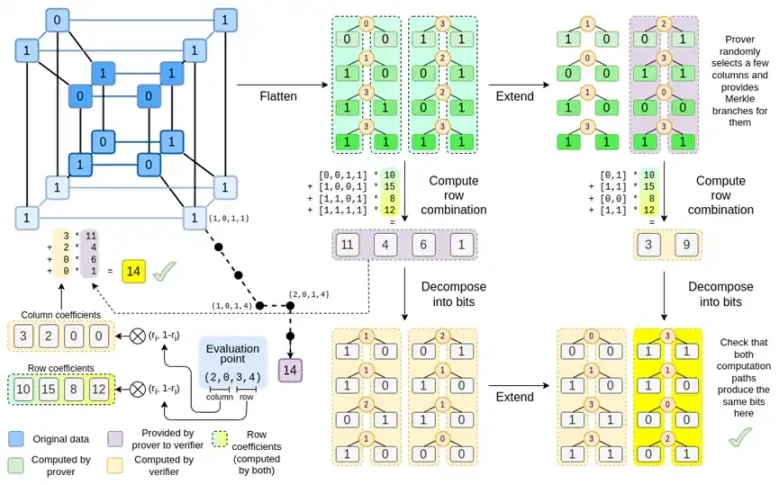
In Binius arbeiten wir an einem multilinearen Polynom: einem Hyperwürfel P(x0, x1,…xk), bei dem die einzelnen Auswertungen P(0, 0, 0, 0), P(0, 0, 0, 1) bis P(1, 1, 1, 1) die Daten enthalten, die uns interessieren. Um eine Berechnung an einem bestimmten Punkt zu beweisen, interpretieren wir dieselben Daten als Quadrat neu. Anschließend erweitern wir jede Zeile mithilfe der Reed-Solomon-Kodierung, um die für die Sicherheit gegen randomisierte Merkle-Zweigabfragen erforderliche Datenredundanz bereitzustellen. Anschließend berechnen wir zufällige lineare Kombinationen der Zeilen und gestalten die Koeffizienten so, dass die neue kombinierte Zeile tatsächlich den berechneten Wert enthält, der uns interessiert. Diese neu erstellte Zeile (neu interpretiert als 128-Bit-Zeile) und einige zufällig ausgewählte Spalten mit Merkle-Zweigen werden an den Prüfer übergeben.

Der Prüfer führt dann die erweiterte Zeilenkombination (oder genauer gesagt die erweiterten Spalten) und die erweiterte Zeilenkombination aus und überprüft, ob die beiden übereinstimmen. Anschließend berechnet er eine Spaltenkombination und überprüft, ob sie den vom Beweiser behaupteten Wert zurückgibt. Dies ist unser Beweissystem (oder genauer gesagt das polynomische Commitment-Schema, das eine Schlüsselkomponente des Beweissystems darstellt).

Was haben wir noch nicht behandelt?

• Um den Validator tatsächlich rechnerisch effizient zu machen, ist ein effizienter Algorithmus zum Erweitern der Zeilen erforderlich. Wir verwenden die hier beschriebene schnelle Fourier-Transformation für binäre Felder (obwohl die genaue Implementierung anders sein wird, da dieser Beitrag eine weniger effiziente Konstruktion verwendet, die nicht auf rekursiver Erweiterung basiert).

• Arithmetisch. Univariate Polynome sind praktisch, weil Sie Dinge wie F(X+2)-F(X+1)-F(X) = Z(X)*H(X) tun können, um benachbarte Schritte in der Berechnung zu verknüpfen. Im Hyperwürfel ist der nächste Schritt viel weniger gut erklärt als X+1. Sie können X+k, Potenzen von k, tun, aber dieses Sprungverhalten geht auf Kosten vieler der wichtigsten Vorteile von Binius. Das Binius-Papier beschreibt die Lösung. Siehe Abschnitt 4.3), aber das ist an sich schon ein tiefes Kaninchenloch.

• So führen Sie sicher bestimmte Wertprüfungen durch. Das Fibonacci-Beispiel erforderte die Überprüfung wichtiger Randbedingungen: der Werte von F(0)=F(1)=1 und F(100). Für das ursprüngliche Binius ist es jedoch unsicher, Prüfungen an bekannten Berechnungspunkten durchzuführen. Es gibt einige recht einfache Möglichkeiten, bekannte Berechnungsprüfungen in unbekannte Berechnungsprüfungen umzuwandeln, indem sogenannte Summenprüfungsprotokolle verwendet werden; diese werden hier jedoch nicht behandelt.

• Lookup-Protokolle, eine weitere Technologie, die in letzter Zeit weit verbreitet ist, werden verwendet, um hocheffiziente Beweissysteme zu erstellen. Binius kann in Verbindung mit Lookup-Protokollen für viele Anwendungen verwendet werden.

• Über die Verifizierungszeit von Quadratwurzeln hinaus. Quadratwurzeln sind teuer: Ein Binius-Beweis von 2^32 Bit ist etwa 11 MB lang. Sie können dies kompensieren, indem Sie andere Beweissysteme verwenden, um Beweise von Binius-Beweisen zu erstellen. Dadurch erhalten Sie die Effizienz eines Binius-Beweises bei geringerer Beweisgröße. Eine weitere Option ist das komplexere FRI-Binius-Protokoll, das einen Beweis mit multilogarithmischer Größe erstellt (genau wie normales FRI).

• Wie Binius die SNARK-Freundlichkeit beeinflusst. Die grundlegende Zusammenfassung ist, dass Sie sich bei Verwendung von Binius nicht mehr darum kümmern müssen, Berechnungen arithmetikfreundlich zu gestalten: Normales Hashing ist nicht mehr effizienter als traditionelles arithmetisches Hashing, Multiplikation modulo 2 hoch 32 oder modulo 2 hoch 256 ist nicht mehr so mühsam wie Multiplikation modulo 2 usw. Aber das ist ein komplexes Thema. Viele Dinge ändern sich, wenn alles binär gemacht wird.

Ich erwarte in den kommenden Monaten weitere Verbesserungen bei der auf binären Feldern basierenden Beweistechnologie.

Dieser Artikel stammt aus dem Internet: Vitalik: Binius, effiziente Beweise für binäre Felder

Verbunden: BNB-Münze zeigt Anzeichen einer Erholung: Neues Jahreshoch in Sicht

Kurz gesagt: Der BNB-Preis erholte sich von $550 und näherte sich dem Durchbrechen des Widerstands von $593. Die Preisindikatoren haben die bullische Dynamik wiedererlangt, was einen Anstieg von 8% unterstützt. Die Sharpe-Ratio von 4,03 wird wahrscheinlich neue Investoren zum Börsen-Token treiben. Der März war ein günstiger Monat für BNB Coin, wobei die Kryptowährung innerhalb weniger Tage zwei neue Jahreshöchststände erreichte, bevor sie eine Korrektur erfuhr. Nach einer fast zweiwöchigen Erholungsphase zeigt BNB Coin Anzeichen dafür, dass es 2024 möglicherweise einen neuen Höchststand erreichen könnte. Aber ist ein solcher Meilenstein erreichbar? BNB sieht vielversprechend aus Nach einer Erholung vom Unterstützungsniveau von $550 ist der Wert von BNB Coin zum Zeitpunkt dieser Analyse auf $581 gestiegen. Diese Verbesserung spiegelt eine Erholung des Risiko-Rendite-Profils des Altcoins wider,…