Analyse der Cross-Chain-Technologie von Bitcoin und Layer2-Assets

Originaltitel: Adaptersignaturen und ihre Anwendung auf Cross-Chain Atomic Swaps

Originallink: https://blog.bitlayer.org/Adaptor_Signatures_and_Its_Application_to_Cross-Chain_Atomic_Swaps/

Originalautor: mutourend, lynndell

1 Einleitung

Mit der rasanten Entwicklung der Layer-2-Skalierungslösung von Bitcoin hat die Häufigkeit von kettenübergreifenden Vermögensübertragungen zwischen Bitcoin und seinem Layer-2-Gegenstück deutlich zugenommen. Dieser Trend wird durch die höhere Skalierbarkeit, die niedrigeren Transaktionsgebühren und den hohen Durchsatz von Layer-2-Technologien wie Bitlayer vorangetrieben. Diese Fortschritte ermöglichen effizientere und wirtschaftlichere Transaktionen und fördern so die breitere Akzeptanz und Integration von Bitcoin in verschiedene Anwendungen. Infolgedessen wird die Interoperabilität zwischen Bitcoin- und Layer-2-Netzwerken zu einer Schlüsselkomponente des Kryptowährungs-Ökosystems, die Innovationen vorantreibt und den Benutzern vielfältigere und leistungsfähigere Finanzinstrumente bietet.

Wie in Tabelle 1 dargestellt, gibt es drei typische Lösungen für Cross-Chain-Transaktionen zwischen Bitcoin und Layer 2, nämlich zentralisierte Cross-Chain-Transaktionen, BitVM Cross-Chain Bridge und Cross-Chain Atomic Swaps. Diese drei Technologien unterscheiden sich in Bezug auf Vertrauensannahmen, Sicherheit, Komfort, Transaktionsbeträge usw. und können unterschiedliche Anwendungsanforderungen erfüllen.

Tabelle 1. Vergleich von Cross-Chain-Transaktionstechnologien

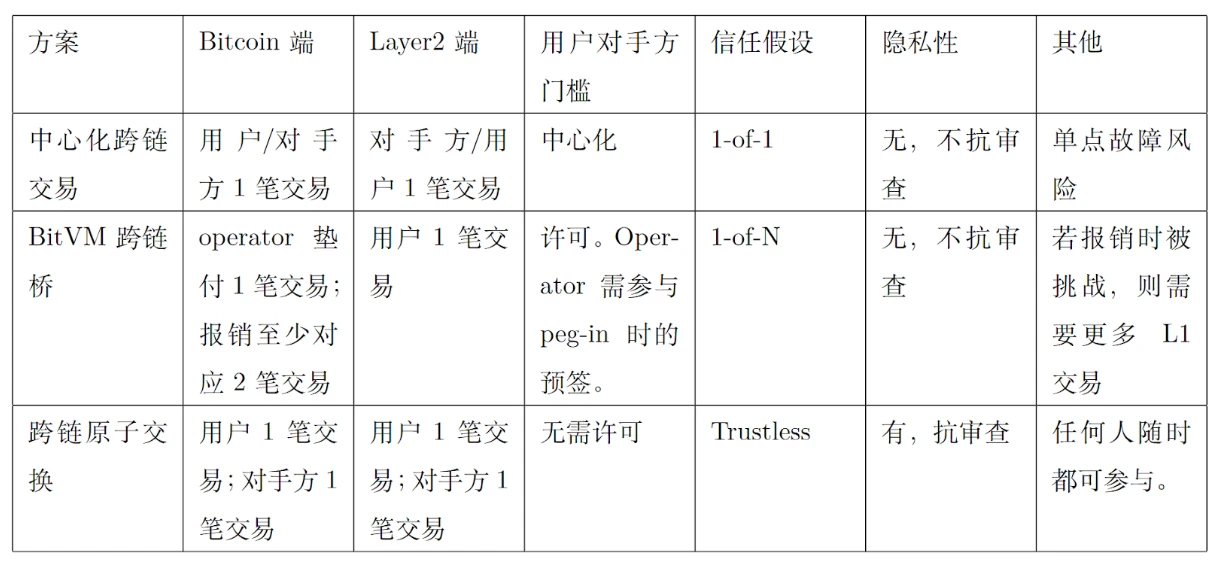
Zentralisierte Cross-Chain-Transaktionen: Benutzer zahlen zunächst Bitcoin an eine zentralisierte Institution (z. B. eine Projektpartei oder Börse), und die zentralisierte Institution zahlt die entsprechenden Vermögenswerte an die vom Benutzer im Layer-2-Netzwerk angegebene Adresse, wodurch die kettenübergreifende Vermögensübertragung abgeschlossen wird. Der Vorteil dieser Technologie besteht darin, dass sie schnell ist und der Zuordnungsprozess relativ einfach ist, da die zentralisierte Institution die Transaktion schnell bestätigen und verarbeiten kann. Die Sicherheit dieser Methode hängt jedoch vollständig von der Zuverlässigkeit und dem Ruf der zentralisierten Institution ab. Wenn bei der zentralisierten Institution technische Fehler, böswillige Angriffe oder Zahlungsausfälle auftreten, sind die Gelder des Benutzers einem hohen Risiko ausgesetzt. Darüber hinaus können zentralisierte kettenübergreifende Transaktionen auch die Privatsphäre des Benutzers gefährden, und Benutzer müssen bei der Auswahl dieser Methode sorgfältig abwägen. Obwohl ihre Bequemlichkeit und Effizienz den Benutzern großen Komfort bieten, sind Sicherheit und Vertrauen die Hauptherausforderungen für zentralisierte kettenübergreifende Transaktionen.

BitVM Cross-Chain-Brücke: Diese Technologie ist relativ komplex. Zunächst zahlen Benutzer in der Peg-in-Phase Bitcoin an die von der BitVM Alliance kontrollierte Multisignaturadresse, um Bitcoin zu sperren. Die entsprechende Anzahl von Token wird in Layer 2 geprägt und der Token wird zur Implementierung von Layer-2-Transaktionen und -Anwendungen verwendet. Wenn der Benutzer den Layer-2-Token zerstört, zahlt der Betreiber die Zahlung vor. Anschließend erstattet der Betreiber die entsprechende Anzahl von Bitcoins an den von der BitVM Alliance kontrollierten Multisignaturpool zurück. Um zu verhindern, dass der Betreiber Böses tut, verwendet der Rückerstattungsprozess einen optimistischen Herausforderungsmechanismus, d. h. jede dritte Partei kann böswilliges Rückerstattungsverhalten anfechten und das böse Verhalten vereiteln. Diese Technologie führt einen optimistischen Herausforderungsmechanismus ein, sodass die Technologie relativ komplex ist. Darüber hinaus umfasst der optimistische Herausforderungsmechanismus eine große Anzahl von Herausforderungs- und Antworttransaktionen und die Transaktionsgebühr ist hoch. Daher ist die BitVM-Cross-Chain-Brücke nur für extrem große Transaktionen geeignet, ähnlich der Ausgabe von U, und hat daher eine geringe Nutzungshäufigkeit.

Atomischer Austausch zwischen Ketten: Ein Atomic Swap ist ein Vertrag, der dezentrale Kryptowährungstransaktionen ermöglicht. In diesem Zusammenhang bedeutet atomar, dass ein Eigentümerwechsel eines Vermögenswerts tatsächlich einen Eigentümerwechsel eines anderen Vermögenswerts bedeutet. Das Konzept wurde erstmals 2013 von TierNolan im Bitcointalk-Forum vorgeschlagen. 4 Jahre lang blieben Atomic Swaps im theoretischen Bereich. Erst 2017 waren Decred und Litecoin die ersten Blockchain-Systeme, die Atomic Swaps erfolgreich durchführten. An einem Atomic Swap müssen zwei Parteien beteiligt sein, und keine dritte Partei kann den Austauschprozess unterbrechen oder stören. Dies bedeutet, dass die Technologie dezentralisiert und unzensierbar ist, einen guten Datenschutz bietet und hochfrequente Cross-Chain-Transaktionen durchführen kann, die bei dezentralen Börsen weit verbreitet sind. Derzeit erfordern Cross-Chain-Atomic Swaps 4 Transaktionen und einige Schemata versuchen, die Anzahl der Transaktionen auf 2 zu komprimieren, aber dies erhöht die Echtzeit-Online-Anforderungen für beide Parteien des Austauschs. Schließlich umfasst die Cross-Chain-Atomic-Swap-Technologie hauptsächlich Hash-Time-Locks und Adaptersignaturen.

Cross-Chain Atomic Swaps basierend auf Hash Time Locks (HTLCs): Das erste Projekt, das erfolgreich Cross-Chain-Atomic-Swaps implementiert hat, ist Decred, das Hash-Locks und Time-Locks verwendet, um den von TierNolan vorgeschlagenen Atomic-Swap mithilfe von On-Chain-Skripten (oder Smart Contracts) umzusetzen. HTLC ermöglicht es zwei Benutzern, zeitlich begrenzte Kryptowährungstransaktionen durchzuführen, d. h. der Empfänger muss dem Vertrag innerhalb einer bestimmten Zeit (bestimmt durch die Anzahl der Blöcke oder die Blockhöhe) einen kryptografischen Beweis (Geheimnis) vorlegen, andernfalls werden die Gelder an den Absender zurückgesendet. Wenn der Empfänger die Zahlung bestätigt, ist die Transaktion erfolgreich. Daher müssen beide teilnehmenden Blockchains über Hash-Lock- und Time-Lock-Funktionen verfügen.

Während HTLC-Atomtausche einen großen Durchbruch im Bereich der dezentralen Austauschtechnologie darstellen, gibt es die folgenden Probleme. Diese Atomtauschtransaktionen und die damit verbundenen Daten werden alle on-chain durchgeführt, was zu einem Verlust der Privatsphäre der Benutzer führt. Mit anderen Worten: Bei jedem Tausch erscheint derselbe Hashwert auf beiden Blockchains, nur wenige Blöcke voneinander entfernt. Dies bedeutet, dass ein Beobachter die am Tausch beteiligten Währungen verknüpfen kann, indem er den gleichen Hashwert in Blöcken findet, die nahe beieinander liegen (Zeitstempel-mäßig). Beim Verfolgen von Währungen über Ketten hinweg ist es einfach, die Quelle zu ermitteln. Obwohl diese Analyse keine relevanten Identitätsdaten preisgibt, können Dritte leicht auf die Identitäten der beteiligten Teilnehmer schließen.

Cross-Chain Atomic Swaps basierend auf Adaptersignaturen: Die zweite Art von Swap, die von BasicSwap angeboten wird, heißt Adapter Signature Atomic Swap und basiert auf einem Paper des Monero-Entwicklers Joël Gugger aus dem Jahr 2020 mit dem Titel Bitcoin-Monero Cross-Chain Atomic Swap . Man kann sagen, dass das Papier eine Umsetzung des Papiers von Lloyd Fourniers aus dem Jahr 2019 ist. Einmalig verifizierbar verschlüsselte Signaturen, auch Adaptersignaturen genannt . Eine Adaptersignatur ist eine zusätzliche Signatur, die mit der ursprünglichen Signatur kombiniert wird, um geheime Daten preiszugeben. Dadurch können sich zwei Parteien gleichzeitig gegenseitig zwei Daten offenbaren. Sie ist eine Schlüsselkomponente des skriptlosen Protokolls, das atomare Swap-Paare von Monero ermöglicht.

Im Vergleich zu HTLC-Atomtauschen haben Adaptersignatur-basierte Atomtausche drei Vorteile: Erstens ersetzt das Adaptersignaturtauschschema die On-Chain-Skripte, auf die sich der geheime Hashtausch stützt, einschließlich Zeitsperren und Hashsperren. Mit anderen Worten, das Geheimnis und der geheime Hash im HTLC-Tausch haben im Adaptersignaturtausch keine direkte Entsprechung. Daher wird es in der Bitcoin-Forschungsgemeinschaft als Skriptloses Skript bezeichnet. Da solche Skripte nicht beteiligt sind, wird außerdem der in der Kette belegte Platz reduziert, wodurch Adaptersignatur-basierte Atomtausche leichter und billiger werden. Schließlich erfordert HTLC, dass jede Kette denselben Hashwert verwendet, während die am Adaptersignatur-Atomtausch beteiligten Transaktionen nicht verknüpft werden können, um Datenschutz zu gewährleisten.

Dieser Artikel stellt zunächst die Schnorr/ECDSA-Adaptersignatur und das Prinzip des Cross-Chain-Atomtauschs vor. Anschließend analysiert er die Sicherheitsprobleme mit Zufallszahlen in der Adaptersignatur sowie die Probleme der Systemheterogenität und Algorithmusheterogenität im Cross-Chain-Szenario und bietet Lösungen. Schließlich wird die Adaptersignatur erweitert und angewendet, um eine nicht-interaktive Verwahrung digitaler Vermögenswerte zu realisieren.

2. Adaptersignaturen und Cross-Chain Atomic Swaps

2.1 Schnorr-Adaptersignaturen und Atomic Swaps

2.2 ECDSA-Adaptersignatur und Atomic Swap

2.2.1 Zero-Knowledge-Beweis zk{v | Ṽ = v ᐧ G, V = v ᐧ Y}

3. Sicherheitsprobleme und -lösungen

3.1 Zufallszahlenprobleme und Lösungen

3.1.1 Problem des Zufallszahlenverlusts

Die Vorsignatur der Schnorr/ECDSA-Adaptersignatur legt die Zufallszahl $r$Ȓ = r ᐧ G fest. Darüber hinaus legt der Zero-Knowledge-Beweis die Zufallszahl $v$ fest, da $Ṽ=v ᐧ G, V=v ᐧ Y$. Wenn die Zufallszahl weitergegeben wird, wird auch der private Schlüssel weitergegeben.

Insbesondere im Schnorr-Protokoll kann die Zufallszahl $r$, wenn sie durchgesickert ist, gemäß der Gleichung wiederhergestellt werden

$ŝ = r + c x.$

Berechnen Sie den privaten Schlüssel $x$.

In ähnlicher Weise kann im ECDSA-Protokoll, wenn die Zufallszahl $r$ durchgesickert ist, diese gemäß der Gleichung erhalten werden

$ŝ = r^{-1 }(hash(m)+R_x x).$

Berechnen Sie den privaten Schlüssel $x$.

Wenn schließlich im Zero-Knowledge-Proof-Protokoll die Zufallszahl $v$ durchsickert, kann sie gemäß der Gleichung erhalten werden

$z := v + c r.$

Berechnen Sie die Zufallszahl $r$ und berechnen Sie dann weiter den privaten Schlüssel $x$ basierend auf der Zufallszahl $r$. Daher muss die Zufallszahl sofort nach der Verwendung gelöscht werden.

3.1.2 Problem der Wiederverwendung von Zufallszahlen

Wenn das Adaptersignaturprotokoll bei zwei beliebigen Cross-Chain-Transaktionen dieselbe Zufallszahl verwendet, führt dies zu einem Verlust des privaten Schlüssels. Insbesondere im Schnorr-Protokoll sind, wenn dieselbe Zufallszahl $r$ verwendet wird, nur $r$ und $x$ im folgenden Gleichungssystem unbekannt:

$ŝ_ 1 =r + c_ 1 x, $

$ ŝ_ 2 = r + c_ 2 x. $

Daher kann das Gleichungssystem gelöst werden, um den privaten Schlüssel $x$ zu erhalten.

Ähnlich verhält es sich im ECDSA-Adaptersignaturprotokoll: Wenn dieselbe Zufallszahl $r$ verwendet wird, sind im folgenden Gleichungssystem nur $r$ und $x$ unbekannt:

$ ŝ_ 1 = r^{-1 }(hash(m_ 1)+R_x x),$

$ ŝ_ 2 = r^{-1 }(hash(m_ 2)+R_x x).$

Daher kann das Gleichungssystem gelöst werden, um den privaten Schlüssel $x$ zu erhalten.

Schließlich sind im Zero-Knowledge-Beweisprotokoll, wenn dieselbe Zufallszahl $v$ verwendet wird, nur $v$ und $r$ im folgenden Gleichungssystem unbekannt:

$z_ 1 = v+c_ 1 r, $

$ z_ 2 = v+c_ 2 r. $

Daher kann das Gleichungssystem gelöst werden, um die Zufallszahl $r$ zu erhalten, und dann kann das Gleichungssystem weiter gelöst werden, um den privaten Schlüssel $x$ zu erhalten.

Wenn verschiedene Benutzer dieselbe Zufallszahl verwenden, wird der private Schlüssel ebenfalls weitergegeben. Mit anderen Worten: Zwei Benutzer, die dieselbe Zufallszahl verwenden, können die Gleichungen lösen und den privaten Schlüssel des jeweils anderen erhalten. Daher sollte RFC 6979 verwendet werden, um das Problem der Wiederverwendung von Zufallszahlen zu lösen.

3.1.3 Lösung: RFC 6979

RFC 6979 spezifiziert eine Methode zum Generieren deterministischer digitaler Signaturen unter Verwendung von DSA und ECDSA, die Sicherheitsprobleme im Zusammenhang mit der Generierung eines Zufallswerts k behebt. Herkömmliche DSA- und ECDSA-Signaturen basieren auf einer Zufallszahl k, die für jeden Signaturvorgang zufällig generiert wird. Wenn diese Zufallszahl wiederverwendet oder falsch generiert wird, ist die Sicherheit des privaten Schlüssels gefährdet. RFC 6979 macht die Generierung einer Zufallszahl überflüssig, indem $k$ deterministisch aus dem privaten Schlüssel und der zu signierenden Nachricht abgeleitet wird. Dadurch wird sichergestellt, dass die Signatur immer dieselbe ist, wenn derselbe private Schlüssel zum Signieren derselben Nachricht verwendet wird, wodurch die Reproduzierbarkeit und Vorhersagbarkeit verbessert wird. Insbesondere wird die deterministische $k$ von HMAC generiert. Der Prozess umfasst eine Hash-Funktion (wie SHA 256), die einen Hash-Wert über den privaten Schlüssel, die Nachricht und einen Zähler berechnet.

$k = SHA 256(sk, msg, Zähler).$

In der obigen Gleichung werden der Einfachheit halber nur der private Schlüssel sk, die Nachricht msg und der Zähler counter gehasht. Der eigentliche Berechnungsprozess in RFC 6979 umfasst weitere Hash-Berechnungen. Diese Gleichung stellt sicher, dass k für jede Nachricht eindeutig ist, während sie für dieselbe Eingabe reproduzierbar ist, und verringert das Risiko einer Offenlegung des privaten Schlüssels, das mit schwachen oder kompromittierten Zufallszahlengeneratoren verbunden ist. Daher bietet RFC 6979 ein leistungsstarkes Framework für deterministische digitale Signaturen unter Verwendung von DSA und ECDSA, löst wichtige Sicherheitsprobleme im Zusammenhang mit der Zufallszahlengenerierung und verbessert die Zuverlässigkeit und Vorhersagbarkeit digitaler Signaturen. Dies macht es zu einem wertvollen Standard für Anwendungen, die hohe Sicherheit erfordern und strenge Betriebsanforderungen erfüllen. Schnorr/ECDSA-Signaturen weisen Zufallszahlenfehler auf, die mithilfe von RFC 6979 verhindert werden müssen. Daher weisen Schnorr/ECDSA-basierte Adaptersignaturen ebenfalls diese Probleme auf, und die Spezifikation von RFC 6979 ist ebenfalls erforderlich, um diese Probleme zu lösen.

3.2 Probleme und Lösungen im kettenübergreifenden Szenario

3.2.1 UTXO- und Kontomodellsystem-Heterogenitätsprobleme und -lösungen

Wie in Abbildung 1 dargestellt, verwendet Bitcoin das UTXO-Modell und implementiert native ECDSA-Signaturen basierend auf der Secp 256k1-Kurve. Bitlayer ist eine EVM-kompatible Bitcoin-L2-Kette, die die Secp 256k1-Kurve verwendet und native ECDSA-Signaturen unterstützt. Die Adaptersignatur implementiert die für den BTC-Austausch erforderliche Logik, während das Bitlayer-Austauschgegenstück durch die leistungsstarken Funktionen von Ethereum-Smart Contracts unterstützt wird.

Cross-Chain-Atomtausche auf Basis von Adaptersignaturen oder zumindest halbskriptlose Adaptersignaturschemata, die für ECDSA-Kurven entwickelt wurden, sind mit Ethereum nicht kompatibel. Der Grund dafür ist, dass Ethereum ein Kontomodell und kein UTXO-Modell ist. Insbesondere erfordern Adaptersignatur-basierte Atomtausche, dass Rückerstattungstransaktionen vorab signiert werden. Im Ethereum-System können Transaktionen jedoch nicht vorab signiert werden, ohne den Nonce zu kennen. Daher kann eine Partei zwischen der Fertigstellung der Vorsignatur und der Ausführung der Transaktion eine Transaktion senden – wodurch die vorab signierte Transaktion ungültig wird (da der Nonce verwendet wurde und nicht wiederverwendet werden kann).

Aus Datenschutzsicht bedeutet dies außerdem, dass Bitlayer-Swaps anonymer sind als HTLCs (der Vertrag steht beiden Parteien im Swap zur Verfügung). Da jedoch eine Partei einen öffentlichen Vertrag haben muss, sind Bitlayer-Swaps weniger anonym als Adaptersignaturen. Auf der Seite ohne Vertrag sieht die Swap-Transaktion wie jede andere Transaktion aus. Auf der Seite mit dem EVM-Vertrag handelt es sich bei der Transaktion jedoch eindeutig um einen Asset-Swap. Obwohl eine Partei einen öffentlichen Vertrag hat, ist es selbst mit ausgefeilten Kettenanalysetools unmöglich, ihn auf eine andere Kette zurückzuführen.

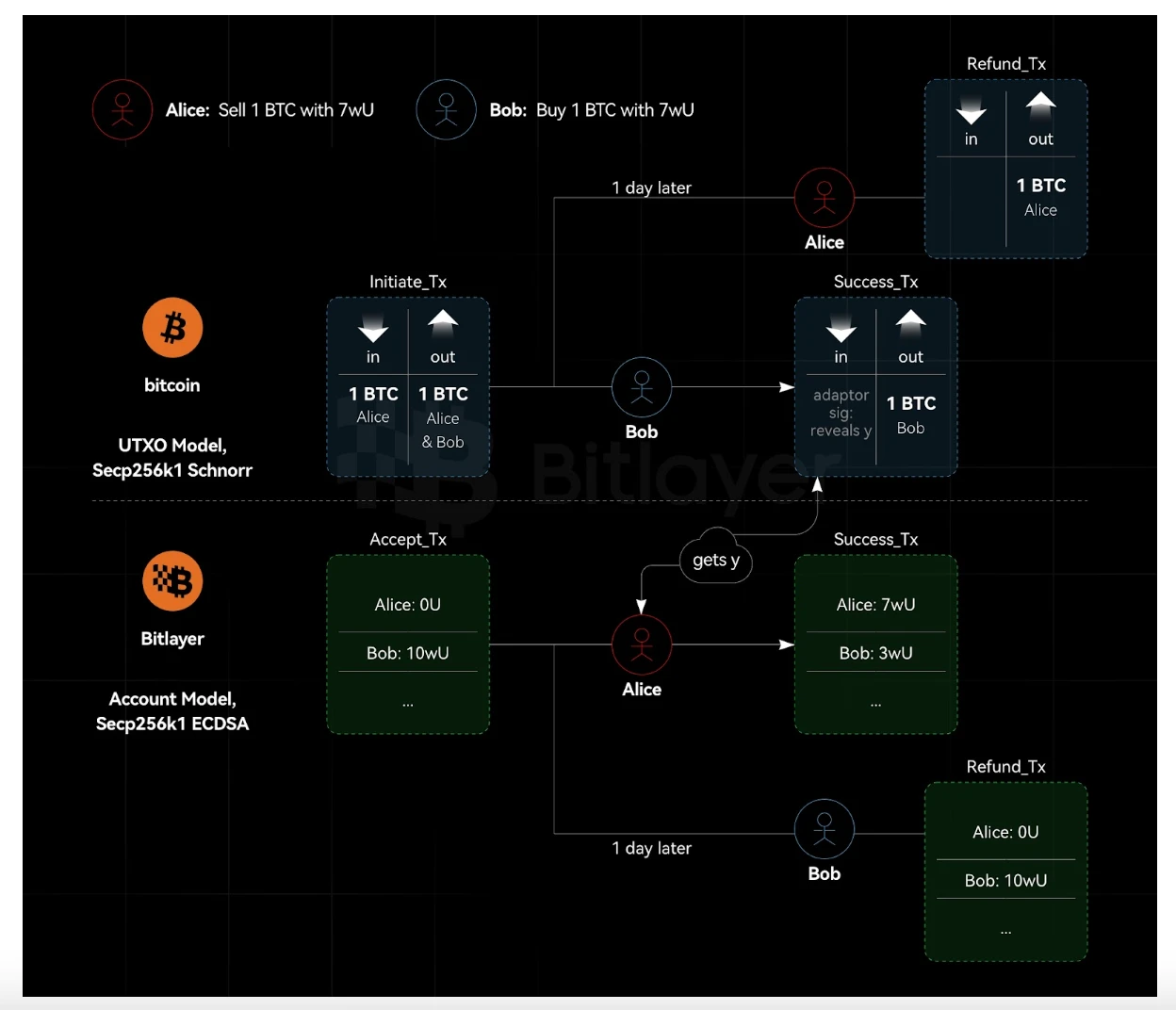
Abbildung 1. UTXO und Kontomodell heterogenes System Cross-Chain Atomic Swap

Bitlayer unterstützt derzeit native ECDSA-Signaturen und kann auch die Schnorr-Signaturüberprüfung über Smart Contracts implementieren. Wenn native Bitlayer-Transaktionen verwendet werden, können Rückerstattungstransaktionen in Atomic Swaps nicht vorab signiert werden; zur Implementierung von Atomic Swaps sind Bitlayer-Smart-Contract-Transaktionen erforderlich. Dieser Prozess geht jedoch zu Lasten der Privatsphäre, d. h. Transaktionen, die an Atomic Swaps im Bitlayer-System teilnehmen, sind nachvollziehbar, können jedoch nicht auf Transaktionen im BTC-System zurückgeführt werden. Dapp-Anwendungen wie Tornado Cash können auf der Bitlayer-Seite entwickelt werden, um Datenschutzdienste für Transaktionen auf der Bitlayer-Seite in Atomic Swaps zwischen BTC und Bitlayer bereitzustellen.

3.2.2 Gleiche Kurve, anderer Algorithmus, Adaptersignatursicherheit

Wie in Abbildung 2 gezeigt, nehmen wir an, dass sowohl Bitcoin als auch Bitlayer die Secp 256 k 1-Kurve verwenden, Bitcoin jedoch Schnorr-Signaturen verwendet, während Bitlayer ECDSA verwendet. In diesem Fall ist die auf Schnorr und ECDSA basierende Adaptersignatur nachweislich sicher. Angenommen, dass bei gegebenen ECDSA- und Schnorr-Signaturorakeln ein Simulator S konstruiert werden kann, um ECDSA zu knacken, dann kann bei nur gegebenem ECDSA-Signaturorakel ein Simulator S konstruiert werden, um ECDSA zu knacken. ECDSA ist jedoch sicher. Ähnlich gilt: Angenommen, dass bei gegebenen ECDSA- und Schnorr-Signaturorakeln ein Simulator S konstruiert werden kann, um Schnorr-Signaturen zu knacken, dann kann bei nur gegebenem ECDSA-Signaturorakel ein Simulator S konstruiert werden, um Schnorr-Signaturen zu knacken. Schnorr-Signaturen sind jedoch sicher. Daher verwendet die Adaptersignatur im Cross-Chain-Szenario dieselbe Kurve, aber der Signaturalgorithmus ist anders, was sicher ist. Mit anderen Worten: Die Adaptersignatur ermöglicht es einem Ende, ECDSA zu verwenden, und dem anderen Ende, Schnorr-Signaturen zu verwenden.

Abbildung 2. Dieselbe Kurve, anderer Algorithmus, andere Adaptersignatur

3.2.3 Unterschiedliche Kurven, unsichere Adaptersignaturen

Angenommen, Bitcoin verwendet die Secp 256 k 1-Kurve und die ECDSA-Signatur, während Bitlayer die ed 25519-Kurve und die Schnorr-Signatur verwendet. In diesem Fall kann die Adaptersignatur nicht verwendet werden. Aufgrund der unterschiedlichen Kurven ist die Reihenfolge der elliptischen Kurvengruppe unterschiedlich, d. h. der Modulkoeffizient ist unterschiedlich. Wenn Bob $y$ an die ECDSA-Signatur im Bitcoin-System anpasst, berechnet er $s:= ŝ+y$. Zu diesem Zeitpunkt ist der Werteraum von $y$ der Skalarraum der Secp 256 k 1-elliptischen Kurvengruppe. Anschließend muss Alice $y$ verwenden, um eine Schnorr-Signatur auf der ed 25519-elliptischen Kurvengruppe durchzuführen. Der Kofaktor der Kurve ed 25519 beträgt jedoch 8, und der Modulkoeffizient ist nicht gleich dem Modulkoeffizienten der elliptischen Kurvengruppe Secp 256 k 1. Daher ist es unsicher, $y$ zu verwenden, um eine Schnorr-Signatur auf der Kurve ed 25519 durchzuführen.

4. Anwendung zur Verwahrung digitaler Vermögenswerte

An der Verwahrung digitaler Vermögenswerte sind drei Parteien beteiligt: Alice, die Käuferin, Bob, der Verkäufer, und der Verwahrer. Die Verwendung von Adaptersignaturen ermöglicht eine nicht-interaktive Verwahrung digitaler Vermögenswerte mit Schwellenwerten und instanziiert eine Teilmenge von Schwellenwertausgabestrategien ohne Interaktion. Diese Teilmenge besteht aus zwei Arten von Teilnehmern: Teilnehmer, die an der Initialisierung teilnehmen, und Teilnehmer, die nicht an der Initialisierung teilnehmen. Letzterer wird als Verwahrer bezeichnet. Der Verwahrer kann keine beliebigen Transaktionen unterzeichnen, sondern sendet nur Geheimnisse an eine der unterstützten Parteien.

Einerseits kann der Verwahrer nur zwischen mehreren festen Abwicklungstransaktionen wählen und kann keine neue Transaktion mit einer der anderen Parteien unterzeichnen. Daher macht dieser geheime Freigabemechanismus die nicht-interaktive Schwellenwertverwahrung weniger flexibel als die Schwellenwert-Schnorr-Signatur. Andererseits kann mithilfe der Schwellenwert-Schnorr-Signatur eine 2-von-3-Ausgabestrategie festgelegt werden. Das Schwellenwert-Schnorr-Signaturprotokoll erfordert jedoch, dass drei Parteien ein dezentrales Schlüsselgenerierungsprotokoll ausführen. Daher hat das auf Adaptersignatur basierende Vermögensverwahrungsprotokoll den Vorteil, nicht-interaktiv zu sein.

4.1 Nicht-interaktive Vermögensverwahrung auf Basis der Adaptersignatur

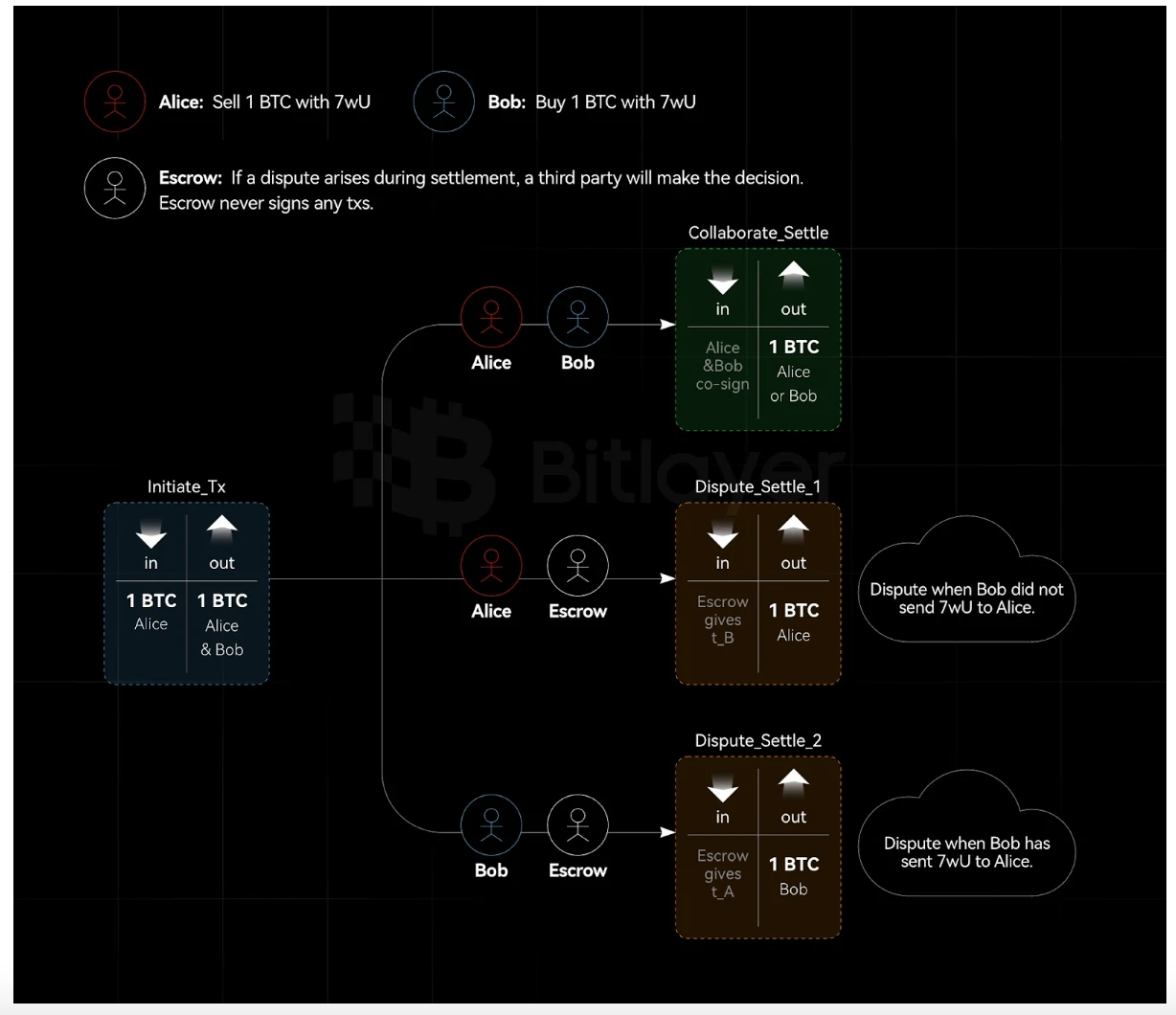
Abbildung 3. Nicht-interaktive Vermögensverwahrung basierend auf der Adaptersignatur

Wie in Abbildung 3 dargestellt, möchten Alice und Bob einen 2-aus-3-Transaktionsoutput mit einer Stealth-Richtlinie erstellen, die einen Verwahrer einschließt. Abhängig von der Bedingung $c$ können Alice oder Bob den Transaktionsoutput ausgeben. Wenn es zu einem Streit zwischen Alice und Bob kommt, entscheidet der Verwahrer (öffentlicher Schlüssel ist $E$, privater Schlüssel ist $e$), ob Alice oder Bob den Vermögenswert erhält.

• Erstellen Sie eine unsignierte Finanzierungstransaktion, um BTC an einen 2-von-2-MuSig-Ausgang zwischen Alice und Bob zu senden.

• Alice wählt einen zufälligen Wert $t_A$ und sendet eine Schnorr-Vorsignatur $(hat{R}_A,hat{s}_A)$ einer Transaktion mit einem Adapter von $t_A ᐧ G$ an Bob. Diese Transaktion sendet die Finanzierungsausgabe an Bob. Alice sendet Bob auch einen Geheimtext, der ein nachweislich verschlüsseltes $C = Enc(E_c, t_A)$ des Geheimnisses $t_A$ enthält und den öffentlichen Treuhandschlüssel $E$ an $E_c = E + hash(E, c)G$ anpasst. Während dieses Vorgangs fügt Bob, nachdem er Alices Vorsignatur erhalten hat, seine eigene Signatur hinzu, die 2-aus-2-MuSig nicht erfüllt und die Finanzierungsausgabe nicht ausgeben kann. Die Finanzierungsausgabe kann nur ausgegeben werden, wenn Bob $t_A$ kennt (bereitgestellt vom Treuhänder) oder Alice eine vollständige Signatur unterschreibt und diese an Bob sendet.

• Entsprechend wiederholt Bob Schritt (2) basierend auf seinem Adaptergeheimnis $t_B$. Zu diesem Zeitpunkt sendet die von Bob signierte Transaktion die Finanzierungsausgabe an Alice.

• Alice und Bob überprüfen beide die Gültigkeit des empfangenen Geheimtexts, bestätigen, dass der Geheimtext eine Verschlüsselung des Geheimnisses $E_c$ ist, und signieren und senden dann die Finanzierungstransaktion. Durch die überprüfbare Verschlüsselung ist die Teilnahme eines Verwalters an der Einrichtungsphase nicht mehr erforderlich und ein öffentlicher Vertrag $c$ ist nicht erforderlich.

• Im Streitfall können Alice und Bob den Geheimtext und die Bedingung c an den Verwalter senden, der dann basierend auf der tatsächlichen Situation eine Entscheidung treffen und den angepassten privaten Schlüssel $e+hash(E, c)$ verwenden kann, um $t_A/t_B$ zu entschlüsseln und an Bob/Alice zu senden.

Wenn es keinen Streit gibt, können Alice und Bob die 2-aus-2-MuSig-Ausgabe nach Belieben ausgeben. Wenn es einen Streit gibt, kann jede Partei den Verwalter kontaktieren und dessen Adaptergeheimnis $t_A$ oder $t_B$ anfordern. Dann kann eine der Parteien mit Hilfe des Verwalters die Adaptersignatur vervollständigen und die Abrechnungstransaktion senden.

4.2 Nachweisbare Verschlüsselung

Praktische verifizierbare Verschlüsselung und Entschlüsselung diskreter Logarithmen kann nicht mit Secp 256 k 1-Adaptern verwendet werden, da diese nur die Überprüfung speziell strukturierter Gruppen unterstützen.

Derzeit gibt es zwei vielversprechende Möglichkeiten zur verifizierbaren Verschlüsselung auf Basis des diskreten Logarithmus von Secp 256k1, nämlich Reinigen Und Jonglieren .

Reinigen wurde ursprünglich vorgeschlagen, um ein MuSig-Protokoll mit einem deterministischen Nonce (DN) zu erstellen, bei dem jeder Unterzeichner einen Zero-Knowledge-Beweis verwenden muss, dass sein Nonce das Ergebnis der korrekten Anwendung einer Pseudozufallsfunktion (PRF) auf den öffentlichen Schlüssel und die Nachricht ist. Purify PRF kann effizient in der Rechenschaltung des Bulletproofs Zero-Knowledge-Protokolls implementiert werden, um ein überprüfbares Verschlüsselungsschema für diskrete Logarithmen auf Secp 256 k 1 zu erstellen. Mit anderen Worten wird eine überprüfbare Verschlüsselung mit zkSnark erreicht.

Jonglieren Die Verschlüsselung umfasst vier Schritte: (1) Teilen Sie den diskreten Logarithmus $x$ in mehrere Segmente $x_k$ der Länge $l$, sodass $x = Summe _k 2 ^{(k-1)l} x_k$; (2) Verwenden Sie den öffentlichen Schlüssel $Y$, um die ElGamal-Verschlüsselung ${ D_k, E_k} = { x_k ᐧ G + r_k ᐧ Y, r_k ᐧ G }$ auf dem Segment $x_k ᐧ G$ durchzuführen; (3) Erstellen Sie für jedes $x_k ᐧ G$ einen Bereichsbeweis, um zu beweisen, dass $D_k$ eine Pedersen-Verpflichtung $x_k ᐧ G + r_k ᐧ Y$ ist und sein Wert kleiner als $ 2 ^l$ ist; (4) Verwenden Sie das Sigma-Protokoll, um zu beweisen, dass ${sum D_k, sum E_k}$ die korrekte Verschlüsselung von $x_k ᐧ G$ ist.

Während des Entschlüsselungsprozesses wird ${D_k, E_k}$ entschlüsselt, um jeweils $x_k ᐧ G$ zu erhalten, und dann wird $x_k$ (mit einem Wertebereich von $[ 0, 2 ^l)$) erschöpfend durchsucht.

Purify muss in Bulletproofs eine PRF ausführen, was relativ kompliziert ist, während Juggling theoretisch einfacher ist. Darüber hinaus ist der Unterschied zwischen den beiden in Bezug auf Proofgröße, Proofzeit und Verifizierungszeit sehr gering.

5. Fazit

Dieser Artikel beschreibt die Prinzipien von Schnorr/ECDSA-Adaptersignaturen und Cross-Chain-Atomtausch im Detail. Er analysiert eingehend die Probleme von Adaptersignaturen mit Zufallszahlenlecks und Duplizierung und schlägt vor, RFC 6979 zu verwenden, um diese Probleme zu lösen. Darüber hinaus analysiert er im Detail die Unterschiede zwischen dem UTXO-Modell der Blockchain und dem Kontomodell in Cross-Chain-Anwendungsszenarien und untersucht auch, ob die Adaptersignatur unterschiedliche Algorithmen und Kurven unterstützt. Schließlich wird die Adaptersignatur erweitert, um eine nicht-interaktive Verwahrung digitaler Vermögenswerte zu realisieren, und die beteiligten kryptografischen Grundelemente – überprüfbare Verschlüsselung – werden kurz vorgestellt.

Referenzen

• Gugger J. Bitcoin-Monero Cross-Chain Atomic Swap[J]. Cryptology ePrint Archive, 2020.

• Fournier L. Einmalig verifizierbar verschlüsselte Signaturen, auch Adaptersignaturen genannt[J]. 2019, 2019.

• https://crypto-in-action.github.io/ecdsa-blockchain-dangers/190816-secp256k1-ecdsa-dangers.pdf

• Pornin T. Deterministische Verwendung des Digital Signature Algorithm (DSA) und des Elliptic Curve Digital Signature Algorithm (ECDSA)[R]. 2013.

• Komlo C, Goldberg I. FROST: flexible rundenoptimierte Schnorr-Schwellenwertsignaturen[C]//Selected Areas in Cryptography: 27. Internationale Konferenz, Halifax, NS, Kanada (virtuelle Veranstaltung), 21.-23. Oktober 2020, Revised Selected Papers 27. Springer International Publishing, 2021: 34-65.

• https://github.com/BlockstreamResearch/scriptless-scripts/blob/master/md/NITE.md

• https://particl.news/the-dex-revolution-basicswap-and-private-ethereum-swaps/

• Camenisch J, Shoup V. Praktisch verifizierbare Verschlüsselung und Entschlüsselung diskreter Logarithmen[C]//Jährliche Internationale Kryptologiekonferenz. Berlin, Heidelberg: Springer Berlin Heidelberg, 2003: 126-144.

• Nick J, Ruffing T, Seurin Y, et al. MuSig-DN: Schnorr-Multisignaturen mit nachweislich deterministischen Nonces[C]//Proceedings der 2020 ACM SIGSAC-Konferenz zu Computer- und Kommunikationssicherheit. 2020: 1717-1731.

• Shlomovits O, Leiba O. Jugglingswap: skriptlose atomare Cross-Chain-Swaps[J]. arXiv-Vorabdruck arXiv: 2007.14423, 2020.

Dieser Artikel stammt aus dem Internet: Analyse der Bitcoin- und Layer2-Asset-Cross-Chain-Technologie

Verwandte Themen: Voller Bargeld, ziehen Sie Bilanz über die brillanten Leistungen von Warren Buffett, dem Meister der Flucht, in den letzten 20 Jahren

Originaltitel: Buffetts erstaunlicher Schachzug wieder! Berkshires Bargeld übertrifft den Marktwert von Ethereum und blickt auf seinen 20-jährigen brillanten Rekord zurück, der Spitze zu entkommen. Originalautor: James, BlockTempo Berkshire Hathaway, eine Investmentgesellschaft im Besitz von Warren Buffett, veröffentlichte letzten Samstag ihren Finanzbericht für das zweite Quartal 2024, aus dem hervorgeht, dass das Unternehmen seinen Apple-Anteil im zweiten Quartal um fast 501 TP9T reduzierte und seine Bargeldposition um 1 TP10T276,9 Milliarden US-Dollar anstieg und damit einen neuen historischen Höchststand erreichte. Zu dieser Zeit glaubten einige Analysten, dass Buffetts massiver Verkauf von Apple-Aktien wahrscheinlich auf seinen Pessimismus hinsichtlich der Börse und der Wirtschaftsaussichten zurückzuführen sei, sodass er sich entschied, alles auf Bargeld zu setzen. Jetzt, mit dem Zusammenbruch der US-amerikanischen und asiatischen Aktienmärkte in den letzten Tagen, hat die Community erneut Buffetts Scharfsinn bewundert, der Spitze erfolgreich zu entkommen. Interessanterweise…